Với giải Bài 62 trang 91 Toán lớp 9 chi tiết trong Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán lớp 9 Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp

Bài 62 trang 91 SGK Toán lớp 9 Tập 2: a) Vẽ tam giác đều ABC cạnh a = 3cm.

b) Vẽ đường tròn (O; R) ngoại tiếp tam giác đều ABC. Tính R.

c) Vẽ đường tròn (O; r) nội tiếp tam giác đều ABC. Tính r.

d) Vẽ tiếp tam giác đều IJK ngoại tiếp đường tròn (O; R).

Lời giải:

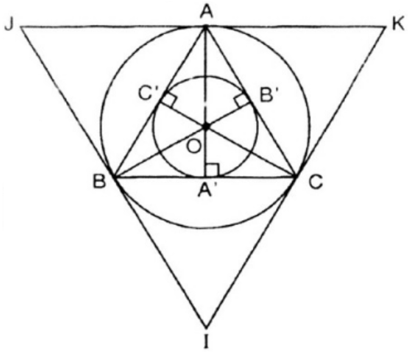
a)

- Dựng đoạn thẳng AB = 3cm

- Dựng cung tròn (A, 3) và cung tròn (B, 3). Hai cung tròn này cắt nhau tại điểm C.

Nối A với C, B với C ta được tam giác đều ABC cạnh 3cm.

b)

Gọi A’, B’, C’ lần lượt là trung điểm của BC, AC, AB

Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba đường trung tuyến, ba đường phân giác AA’, BB’, CC’ của tam giác đều ABC)

Dựng đường trung trực của đoạn thẳng BC và CA

Hai đường trung trực cắt nhau tại O

Vẽ đường tròn tâm O, bán kính R = OA = OB = OC ta được đường tròn ngoại tiếp tam giác ABC

Tính AA’:

Xét tam giác AA’C vuông tại A’ (do AA’ là đường cao)

Có: AC = 3cm

A’ là trung điểm của BC $\Rightarrow A\text{'}C=\frac{1}{2}BC=\frac{3}{2} \left(cm\right)$

Áp dụng định lí Py-ta-go ta có:

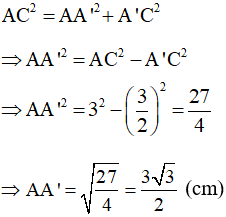
Theo cách dựng, ta có O cũng là trọng tâm tam giác ABC (giao điểm của ba đường trung tuyến)

$\Rightarrow OA=\frac{2}{3}AA\text{'}$$=\frac{2}{3}.\frac{3\sqrt{3}}{2}=\sqrt{3} \left(cm\right)$

Do đó, bán kính đường tròn ngoại tiếp tam giác ABC là: $R=OA=\sqrt{3}$ (cm)

c)

Do tam giác ABC là tam giác đều các trung điểm A’; B’; C’ của các cạnh BC; CA; AB đồng thời là chân đường phân giác hạ từ A, B, C đến BC, AC, AB.

Đường tròn nội tiếp tam giác (O; r) tiếp xúc ba cạnh của tam giác đều ABC tại các trung điểm A’, B’, C’  của các cạnh.

$\Rightarrow r=OA\text{'}=OB\text{'}=OC\text{'}$

Theo cách dựng, ta có O cũng là trọng tâm tam giác ABC (giao điểm của ba đường trung tuyến)

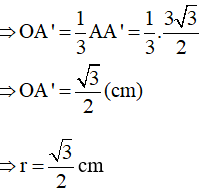
d)

Vẽ các tiếp tuyến với đường tròn (O; R) tại A, B, C. Ba tiếp tuyến này cắt nhau tại I, J, K

Ta có: Tam giác IJK là tam giác đều ngoại tiếp (O; R).