Với giải Bài 61 trang 91 Toán lớp 9 chi tiết trong Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán lớp 9 Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp

Bài 61 trang 91 SGK Toán lớp 9 Tập 2: a) Vẽ đường tròn tâm O, bán kính 2cm.

b) Vẽ hình vuông nội tiếp đường tròn (O) ở câu a).

c) Tính bán kính r của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn (O; r).

Lời giải:

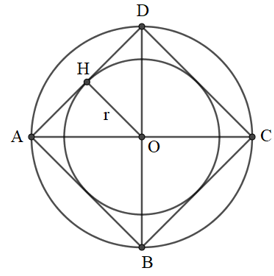
a)

Cách vẽ:

- Chọn điểm O làm tâm, mở compa có độ dài 2cm, vẽ đường tròn tâm O bán kính 2cm

b)

Cách vẽ:

- Vẽ đường kính AC và BD vuông góc với nhau

- Nối A với B, B với C, C với D, D với A ta được tứ giác ABCD là hình vuông nội tiếp đường tròn (O; 2cm)

c)

Kẻ OH vuông góc với AD tại H

Khi đó, OH = r là bán kính của đường tròn nội tiếp hình vuông ABCD.

Vì AB = BC = CD = DA (do ABCD là hình vuông)

nên khoảng cách từ tâm O đến AB, BC, CD, DA bằng nhau và cùng bằng OH (định lý liên hệ giữa dây cung và khoảng cách từ tâm đến dây)

Ta có: Tam giác OAD vuông tại O (do AC vuông góc với BD tại O)

Mà: OA = OD (cùng bằng bán kính đường tròn (O; OA))

Do đó, tam giác OAD vuông cân tại O

Có: OH là đường cao (do OH vuông góc với AD tại H) vừa là đường trung tuyến ứng với cạnh huyền

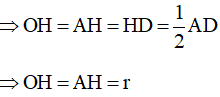
Xét tam giác OHD vuông tại H  (do OH vuông góc với AD tại H)

Áp dụng định lí Py-ta-go ta có:

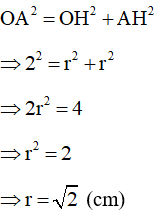
Vẽ đường tròn (O;$\sqrt{2}$cm). Đường tròn này nội tiếp hình vuông ABCD, tiếp xúc cạnh hình vuông tại các trung điểm của mỗi cạnh.