Tìm x và y trong mỗi hình sau

Thanh Trà Ngày: 17-10-2022 Lớp 9

2.2 K

Với giải Bài 8 trang 70 Toán lớp 9 chi tiết trong Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán lớp 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông

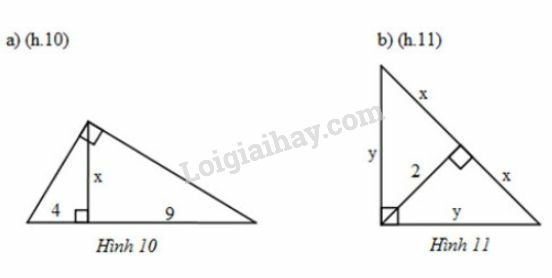
Bài 8 trang 70 SGK Toán 9 Tập 1 :Tìm $x$ và $y$ trong mỗi hình sau:

Giải Toán 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông (ảnh 26)

Giải Toán 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông (ảnh 28)

Phương pháp giải:

a) Dùng hệ thức liên quan đến đường cao và hình chiếu , biết tính được .

b) +) Dùng hệ thức liên quan đến đường cao và hình chiếu

+) Dùng định lí Pytago trong tam giác vuông để tính .

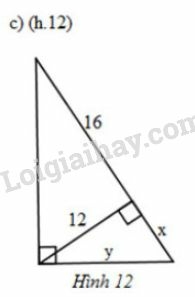
c) Dùng hệ thức liên quan đến đường cao và hình chiếu , biết tính được .

+) Dùng định lí Pytago trong tam giác vuông.

Lời giải:

Đặt tên các điểm như hình vẽ:

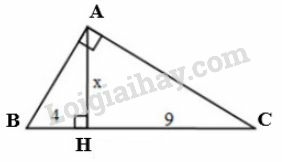
Giải Toán 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông (ảnh 29)

Xét $Δ A B C$ vuông tại $A$ , đường cao $A H$ . Áp dụng hệ thức $h^{2} = b^{'} . c^{'}$ , ta được:

$A H^{2} = B H . C H$

$\Leftrightarrow x^{2} = 4.9 = 36$

$\Leftrightarrow x = \sqrt{36} = 6$

Vậy $x = 6$

b) Đặt tên các điểm như hình vẽ

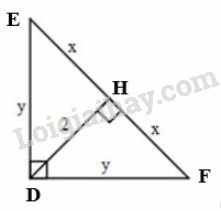
Giải Toán 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông (ảnh 30)

Xét $Δ D E F$ vuông tại $D$ , đường cao $D H$ . Áp dụng hệ thức $h^{2} = b^{'} . c^{'}$ , ta được:

$D H^{2} = H E . H F \Rightarrow 2^{2} = x . x \Rightarrow x^{2} = 4 \Rightarrow x = 2$

Xét $Δ D H F$ vuông tại $H$ . Áp dụng định lí Pytago, ta có:

$D F^{2} = D H^{2} + H F^{2}$

$y^{2} = 2^{2} + x^{2} = 2^{2} + 2^{2} = 8$

$\Rightarrow y = \sqrt{8} = 2 \sqrt{2}$

Vậy $x = 2, y = 2 \sqrt{2}$ .

c) Đặt tên các điểm như hình vẽ:

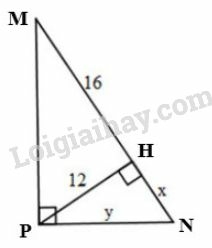
Giải Toán 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông (ảnh 31)

Xét $Δ M N P$ vuông tại $P$ , đường cao $P H$ . Áp dụng hệ thức $h^{2} = b^{'} . c^{'}$ , ta được:

$P H^{2} = H M . H N \Leftrightarrow 12^{2} = 16. x$

$\Leftrightarrow 144 = 16. x$

$\Leftrightarrow x = \frac{144}{16} = 9$

Xét $Δ P H N$ vuông tại $H$ . Áp dụng định lí Pytago, ta có:

$P N^{2} = P H^{2} + H N^{2} \Leftrightarrow y^{2} = 12^{2} + 9^{2}$

$\Leftrightarrow y^{2} = 144 + 81 = 225$

$\Leftrightarrow y = \sqrt{225} = 15$

Vậy $x = 9, y = 15$ .

Từ khóa :

toán 9 Giải bài tập

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 5

Vở bài tập Toán lớp 5 Tập 1 trang 110 Bài 45: Tỉ lệ bản đồ | Cánh diều Lữ Ngọc My My

Toán Lớp 5

Vở bài tập Toán lớp 5 Tập 1 trang 108 Bài 44: Sử dụng máy tính cầm tay | Cánh diều Lữ Ngọc My My

Toán Lớp 5

Vở bài tập Toán lớp 5 Tập 1 trang 106 Bài 44: Sử dụng máy tính cầm tay | Cánh diều Lữ Ngọc My My

Toán Lớp 5

Vở bài tập Toán lớp 5 Tập 1 trang 104 Bài 43: Luyện tập chung | Cánh diều Lữ Ngọc My My