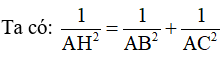Tailieumoi.vn xin giới thiệu Bài tập Toán 9 Chương 1 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 1 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác. Mời các bạn đón xem:
Bài tập Toán 9 Chương 1 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
A. Bài tập Một số hệ thức về cạnh và đường cao trong tam giác
I. Bài tập trắc nghiệm
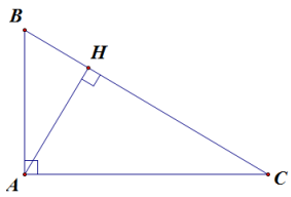
Câu 1: Cho tam giác ABC vuông tại A , đường cao AH (như hình vẽ). Hệ thức nào sau đây là đúng?
A. AH2 = AB.AC
B. AH2 = BH.CH
C. AH2 = AB.BH
D. AH2 = CH.BC
Cho tam giác ABC vuông tại A , đường cao AH . Khi đó ta có hệ thức: HA2 = HB.HC
Chọn đáp án B
Câu 2: Cho tam giác ABC vuông tại A , đường cao AH (như hình vẽ). Hệ thức nào sau đây là sai?
Cho tam giác ABC vuông tại A , đường cao AH . Khi đó ta có các hệ thức:
Chọn đáp án D
Câu 3: Tính x, y trong hình vẽ sau:
A. x = 7,2; y = 11,8
B. x = 7; y = 12
C. x = 7,2; y = 12,8
D. x = 7,2; y = 12
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
Vậy x = 7,2; y = 12,8
Chọn đáp án C
Câu 4: Tính x, y trong hình vẽ sau:
A. x = 3,6; y = 6,4
B. y = 3,6; x = 6,4
C. x = 4; y = 6
D. x = 2; y = 7,2
Theo định lý Pytago ta có:
BC2 = AB2 + AC2 ⇔ BC2 = 100 ⇔ BC = 10
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
Vậy x = 3,6; y = 6,4
Chọn đáp án A
Câu 5: Tính x, y trong hình vẽ sau:
Theo định lý Pytago ta có:
BC2 = AB2 + AC2 ⇔ BC2 = 74
⇔ BC = √74
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
Chọn đáp án A
Câu 6: Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 9cm; CH = 16cm.
Tìm khẳng định sai trong các khẳng định sau:
A. AH = 15 cm
B. AB = 12 cm
C. AC = 20 cm
D. AH = 12 cm
Ta có : BC = BH + HC = 9 + 16 = 25 (cm)
Áp dụng hệ thức về cạnh và đường cao trong tam giác –vuông ta có:
Chọn đáp án A.
Câu 7: Cho tam giác ABC vuông tại A, đường cao AH. Biết AH = 6cm; BH = 4,5 cm.
Tìm khẳng định đúng trong các khẳng định sau ?
A. AB = 10
B. AC = 7,5
C. BC= 12, 5
D. HC = 9
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:
Chọn đáp án C.
Câu 8: Cho tam giác ABC vuông tại A, đường cao AH. Tính diện tích tam giác ABC biết AH = 12 cm; BH = 9cm.
A. 100 cm2
B. 150 cm2
C. 125 cm2
D. 200 cm2
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:
Chọn đáp án B.
Câu 9: Cho tam giác ABC vuông tại A. Biết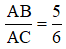 
, đường cao AH = 30 cm. Tính AB?
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:
Chọn đáp án A.
Câu 10: Cho một tam giác vuông. Biết tỉ số hai cạnh góc vuông là 3 : 4 và cạnh huyền là 125cm. Tính độ dài các cạnh của tam giác vuông đã cho?
A. 50 và 75
B. 25 và 75
C. 75 và 100
D.60 và 80
Gọi tam giác vuông đã cho là tam giác ABC vuông tại A; AB < AC và đường cao AH.
Theo giả thiết tỉ số hai cạnh góc vuông là 3 : 4 nên
Do đó, AB = 3.25 = 75 cm và AC = 4.25 = 100cm
Chọn đáp án C.
Câu 11: Tìm x, y trong hình vẽ sau:
A. x = 7,2; y = 11,8
B. x = 7; y = 12
C. x = 7,2; y = 12,8
D. x = 7,2; y = 12
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
Vậy x = 7,2; y = 12,8
Đáp án cần chọn là: C
Câu 12: Tìm x, y trong hình vẽ sau:
A. x = 6,5; y = 9,5
B. x = 6,25; y = 9,75
C. x = 9,25; y = 6,75
D. x = 6; y = 10
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
Vậy x = 6,25; y = 9,75
Đáp án cần chọn là: B
Câu 13: Tìm x trong hình vẽ sau (làm tròn đến chữ số thập phân thứ hai).
A. x ≈ 8,81
B. x ≈ 8,82
C. x ≈ 8,83
D. x ≈ 8,80
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
Vậy x ≈ 8,82
Đáp án cần chọn là: B
Câu 14: Tính x trong hình vẽ sau:
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
Vậy x = 12
Đáp án cần chọn là: C
Câu 15: Cho tam giác ABC vuông tại A, đường cao AH. Cho biết AB : AC = 3 : 4 và AH = 6cm. Tính độ dài các đoạn thẳng CH
A. CH = 8
B. CH = 6
C. CH = 10
D. CH = 12
Ta có: AB : AC = 3 : 4, đặt AB = 3a; AC = 4a (a > 0)
Theo định lý Py-ta-go cho tam giác vuông AHC ta có:
Vậy CH = 8
Đáp án cần chọn là: A
II. Bài tập vận dụng có lời giải
Câu 1: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB:AC = 3:4 và AB + AC = 21cm.
a) Tính các cạnh của tam giác ABC.
b) Tính độ dài các đoạn AH, BH, CH.
Lời giải:
a) Theo giả thiết: AB:AC = 3:4, suy ra
Do đó AB = 3.3 = 9 (cm); AC = 3.4 = 12 (cm).
Tam giác ABC vuông tại A, theo định lý Py – ta – go ta có:
BC2 = AB2 + AC2 = 92 + 122 = 225, suy ra BC = 15cm
b) Tam giác ABC vuông tại A, ta có AH.BC = AB.AC, suy ra
AH2 = BH.HC. Đặt BH = x (0 < x < 9) thì HC = 15 - x, ta có:
(7,2)2 = x(15 - x) ⇔ x2 - 15x + 51,84 = 0 ⇔ x(x - 5,4) = 9,6(x - 5,4) = 0 ⇔ (x - 5,4)(x - 9,6) = 0 ⇔ x = 5,4 hoặc x = 9,6 (loại)
Vậy BH = 5,4cm. Từ đó HC = BC - BH = 9,6 (cm).
Chú ý: Có thể tính BH như sau:
AB2 = BH.BC suy ra
III. Bài tập vận dụng
Câu 1: Cho tam giác cân ABC có đáy BC = 2a , cạnh bên bằng b (b > a) .
a) Tính diện tích tam giác ABC
b) Dựng BK ⊥ AC . Tính tỷ số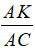 
.
B. Lý thuyết Một số hệ thức về cạnh và đường cao trong tam giác
1. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền
Định lí 1. Trong một tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
Ví dụ 1. Tam giác ABC vuông tại A, đường cao AH.
Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.
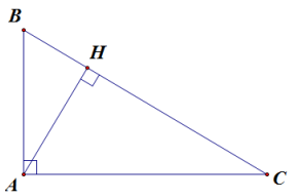
Ta có: AB2 = BC . BH; AC2 = BC . HC.
2. Một số hệ thức liên quan tới đường cao
Định lí 2. Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
Ví dụ 2. Tam giác ABC vuông tại A, đường cao AH.
Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.
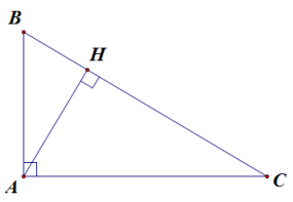
Ta có: AH2 = BH . HC.
Định lí 3. Trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng.
Ví dụ 3. Tam giác ABC vuông tại A, đường cao AH.
Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.
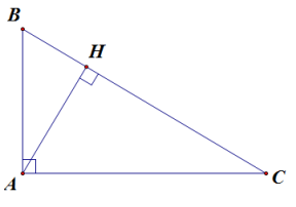
Ta có: AB . AC = BC . AH.
Định lí 4. Trong một tam giác vuông, nghịch đảo của bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông.
Ví dụ 4. Tam giác ABC vuông tại A, đường cao AH.
Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
