Lý thuyết và bài tập tự luyện về Chứng minh hệ thức về cạnh

Lý thuyết và bài tập tự luyện về Chứng minh hệ thức về cạnh - Ôn thi vào lớp 10 chọn lọc

Quý Lê Xuân Ngày: 08-03-2024 Lớp 9

Tải xuống 4 1.8 K 10

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ bài tập Chứng minh hệ thức về cạnh - Ôn thi vào lớp 10, tài liệu bao gồm 4 trang, tuyển chọn bài tập Chứng minh hệ thức về cạnh đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Tài liệu Chứng minh hệ thức về cạnh - Ôn thi vào lớp 10 gồm các nội dung chính sau:

A. Phương pháp giải

- tóm tắt lý thuyết ngắn gọn.

B. Ví dụ minh họa

- gồm 2 ví dụ minh họa đa dạng của các dạng bài tập trên có lời giải chi tiết.

C. Bài tập tự luyện

- gồm 10 bài tập vận dụng giúp học sinh tự rèn luyện cách giải các dạng bài tập Chứng minh hệ thức về cạnh - Ôn thi vào lớp 10.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

Chứng minh hệ thức về cạnh - Ôn thi vào lớp 10 (ảnh 1)

CHỨNG MINH CÁC HỆ THỨC VỀ CẠNH

A. Phương pháp giải

+ Để làm được bài toán này ta có thể sử dụng định lý Ta-lét, tính chất đường phân giác, tam giác đồng dạng, các hệ thức lượng trong tam giác vuông.

+ Các bước suy luận để chứng minh:

- Giả sử cần chứng minh: $AB \cdot AC = AD . AE$

- Ta lập sơ đồ: $A B . A C = A D . A E \Leftarrow \frac{A B}{A D} = \frac{A E}{A C} \Leftarrow Δ A B E ~ Δ A D C$

- Khi đó bước đầu tiên ta sẽ chứng minh tam giác đồng dạng để suy ra các cặp cạnh tương ứng tỉ lệ rồi chứng minh được hệ thức hình học đề bài đã ra

+ Ngoài ra có những bài toán ta sẽ không trực tiếp ra được hệ thức cần chứng minh mà cần phải chứng minh từng vế của hệ thức bằng với một hệ thức thứ ba.

B. Ví dụ minh họa

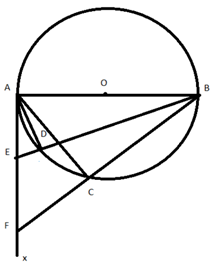
Bài 1: Cho đường tròn tâm O, đường kính AB có bán kính R, tiếp tuyến Ax. Trên tiếp tuyến Ax lấy điểm F sao cho BF cắt đường tròn tại C. Tia phân giác của góc ABF cắt Ax tại E và cắt đường tròn tại D. Chứng minh rằng BD.BE = BC.BF

Hướng dẫn giải

Chứng minh hệ thức về cạnh - Ôn thi vào lớp 10 (ảnh 2)

+ Có $\hat{A C B}$ nhìn đường kính AB nên $\hat{A C B} = 90^{°}$

+ Có Ax là tiếp tuyến, F thuộc Ax nên $\hat{F A B} = 90^{0}$

+ Xét tam giác FAB và tam giác ACB có:

$\hat{B}$ chung

$\hat{A C B} = \hat{F A B} (= 90^{0})$

Suy ra hai tam giác FAB và ACB đồng dạng theo trường hợp góc - góc

$\Rightarrow \frac{A B}{B C} = \frac{B F}{B A} \Rightarrow B C . B F = A B^{2}$ (cặp cạnh tương ứng tỉ lệ) (1)

+ Có $\hat{A D B}$ nhìn đường kính AB nên $\hat{A D B} = 90^{0}$

+ Có Ax là tiếp tuyến, E thuộc Ax nên $\hat{E A B} = 90^{0}$

+ Xét tam giác EAB và tam giác ADB có:

$\hat{\hat{B}}$ : chung

$\hat{A D B} = \hat{E A B} (= 90^{0})$

Suy ra hai tam giác EAB và ADB đồng dạng theo trường hợp góc - góc

$\Rightarrow \frac{B E}{B A} = \frac{A B}{B D} \Rightarrow B E . B D = A B^{2}$ (cặp cạnh tương ứng tỉ lệ)

Từ (1) và (2) suy ra $B C . B F = B E . B D (= A B^{2})$ (đpcm)

Ví dụ 2. Cho đường tròn (O), đường kính AB cố định, điểm I nằm giữa A và O sao cho AI = 2/3 AO. Kẻ dây MN vuông góc với AB tại I, gọi C là điểm tùy ý thuộc cung lớn MN sao cho C không trùng với M, N và B. Nối AC cắt MN tại E. Chứng minh hệ thức: $A M^{2} = A E . A C$ .