Tailieumoi.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
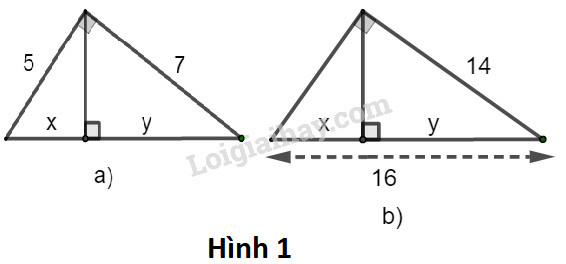
Phương pháp giải:
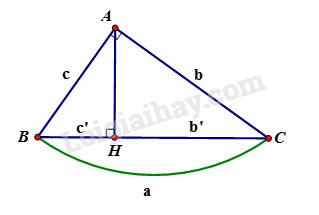
Cho tam giác vuông tại , đường cao . Khi đó ta có các hệ thức sau:
+) hay
+) hay
+) hay (định lý Pytago)
Lời giải:
a) Ta đặt tên như hình vẽ dưới đây:
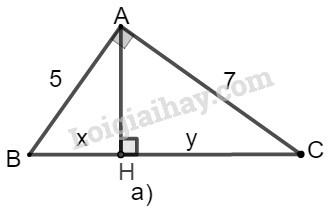
Xét tam giác có chiều cao
Theo định lý Py-ta-go, ta có:
Hay
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu của nó, ta có:
Thay vào , ta có:
Vậy
b) Ta đặt tên như hình vẽ dưới đây:
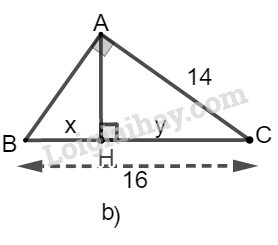
Xét tam giác có chiều cao
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
Mà
Vậy
Phương pháp giải:
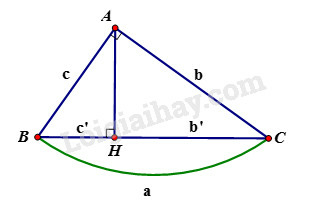
Cho tam giác vuông tại , đường cao . Khi đó ta có các hệ thức sau:
+) hay
+) hay
+) hay
Lời giải:
a) Đặt tên hình như hình dưới đây:
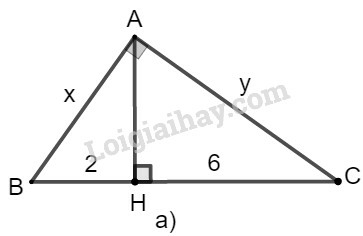
Xét tam giác vuông tại , đường cao
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
hay
hay
b) Đặt tên hình như hình dưới đây:
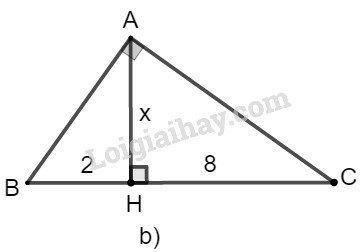
Xét tam giác vuông tại , đường cao
Theo hệ thức liên hệ giữa đường cao và hình chiếu hai cạnh góc vuông, ta có:
hay
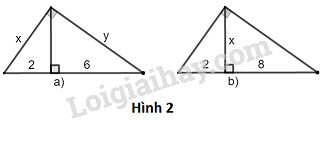
Bài 3 trang 103 SBT Toán 9 tập 1: Hãy tính và trong các hình sau: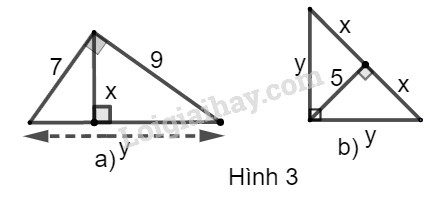
Phương pháp giải:
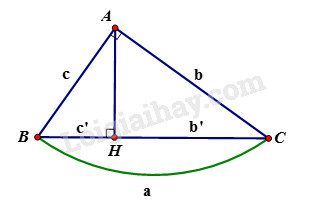
Cho tam giác vuông tại , đường cao . Khi đó ta có các hệ thức sau:
+) hay
+) hay
+) hay (định lý Pytago)
Lời giải:
a) Hình a
Theo định lý Pi-ta-go, ta có:
Theo hệ thức liên hệ giữa đường cao và cạnh trong tam giác vuông, ta có:
b) Hình b
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
Phương pháp giải:
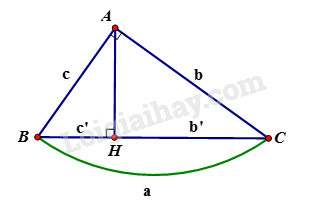
Cho tam giác vuông tại , đường cao . Khi đó ta có các hệ thức sau:
+) hay
+) hay
+)
+) hay (định lý Pytago)
Lời giải:
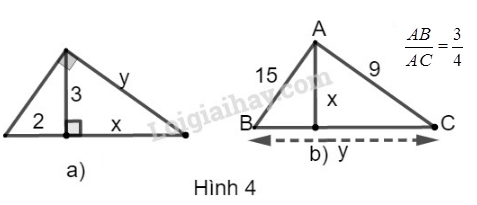
a) Hình a
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
b) Hình b
Ta có:
Theo định lý Pi-ta-go, ta có:
Suy ra:
Theo hệ thức liên hệ giữa đường cao và cạnh trong tam giác vuông, ta có:
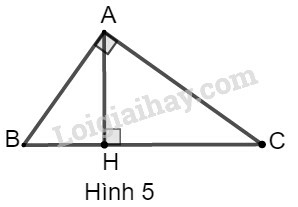
Giải bài toán trong mỗi trường hợp sau:
a) Cho Tính
b) Cho Tính
Phương pháp giải:
Để giải bài toán ta áp dụng các công thức sau:
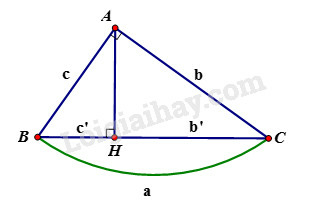
Cho tam giác vuông tại , đường cao . Khi đó ta có các hệ thức sau:
+) hay
+) hay
+)
+) hay (định lý Pytago)
Lời giải:
a)
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
b)
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
Theo hệ thức liên hệ giữa đường cao và hình chiếu cạnh góc vuông, ta có:
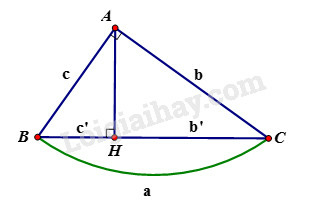
Cho tam giác vuông tại , đường cao . Khi đó ta có các hệ thức sau:
+) hay
+) hay
+)
+) hay (định lý Pytago)
Lời giải:
Ta vẽ được hình dưới đây:
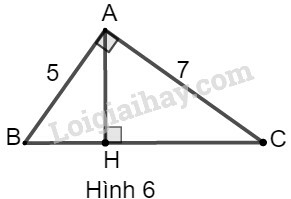
Giả sử tam giác ABC có:
Theo định lý Py-ta-go, ta có:
Theo hệ thức liên hệ giữa đường cao và cạnh trong tam giác vuông, ta có:
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu của nó, ta có:
Bài 7 trang 103 SBT Toán 9 tập 1: Đường cao của một tam giác vuông chia cạnh huyền thành hai đường thẳng có độ dài là 3 và 4. Hãy tính các cạnh góc vuông của tam giác này.
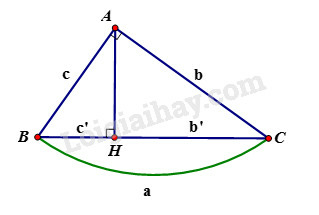
Cho tam giác vuông tại , đường cao . Khi đó ta có các hệ thức sau:
+) hay
+) hay
+) hay (định lý Pytago)
Lời giải:
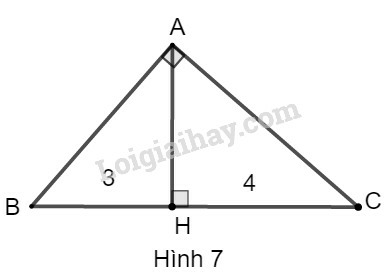
Giả sử tam giác ABC có:
Ta có
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
Bài 8 trang 103 SBT Toán 9 tập 1: Cạnh huyền của một tam giác vuông lớn hơn một cạnh góc vuông là và tổng của hai cạnh góc vuông lớn hơn cạnh huyền . Hãy tính các cạnh của tam giác vuông này.
6
Phương pháp giải:
Xét tam giác vuông tại A.
Để giải bài toán ta thực hiện các bước sau:
Bước 1: Thực hiện liên kết các dữ kiện:
Bước 2: Cộng vế với vế để tìm ra một cạnh trong tam giác.
Bước 3: Sử dụng định lí Pytago để tìm các cạnh còn lại của tam giác.
Lời giải:
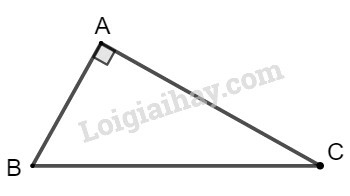
Giả sử tam giác ABC có
Theo đề bài, ta có: (1)
(2)
Từ (1) và (2) suy ra:
Theo định lý Pytago, ta có: (3)
Từ (1) suy ra: (4)
Thay (4) và (3) ta có:
Thay (cm) vào (1) ta có:
Phương pháp giải:
Xét tam giác có và
Suy luận để có
Sử dụng hệ thức:
Từ đó tính được suy ra cạnh và lập luận để có là cạnh nhỏ nhất.
Lời giải:
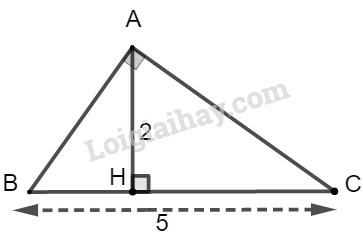
Giả sử tam giác có và
Ta có: nên (1)
Theo hệ thức liên hệ giữa đường cao và các hình chiếu cạnh góc vuông trong tam giác vuông, ta có:
(2)
Từ (1) và (2) suy ra:
Do nên và
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
Suy ra:
Vì nên hay là cạnh nhỏ nhất của tam giác
Bài 10 trang 104 SBT Toán 9 tập 1: Cho một tam giác vuông. Biết tỷ số hai cạnh góc vuông là và cạnh huyền là . Tính độ dài các cạnh góc vuông và hình chiếu của các cạnh góc vuông trên cạnh huyền.Áp dụng tính chất dãy tỉ số bằng nhau:
Cho tam giác vuông tại , đường cao .
Khi đó ta có các hệ thức sau:
+)
+)
+) (định lý Pytago).
Lời giải:
Giả sử vuông tại chiều cao và
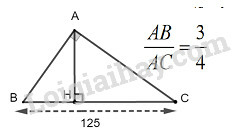
Từ suy ra:
Theo tính chất dãy tỉ số bằng nhau, ta có:
Theo định lí Pytago, ta có:
Từ (1) và (2) suy ra:
Suy ra :
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
Cho tam giác vuông tại , đường cao .
Khi đó ta có các hệ thức sau:
+)
+)
+)
+) (định lý Pytago).
Lời giải:
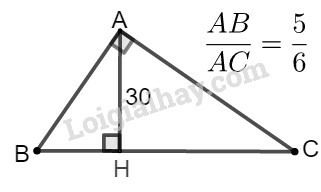
Xét hai tam giác vuông và ta có:
(hai góc cùng phụ )
Vậy (g.g)
Suy ra: (1)
Theo đề bài: và (2)
Từ (1) và (2) suy ra:
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
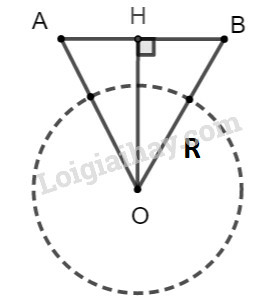
Bài 12 trang 104 SBT Toán 9 tập 1: Hai vệ tinh đang bay ở vị trí và cùng cách mặt đất có nhìn thấy nhau hay không nếu khoảng cách giữa chúng theo đường thẳng là ? Biết rằng bán kính của Trái Đất gần bằng và hai vệ tinh nhìn thấy nhau nếu .
Phương pháp giải:
Sử dụng: Tam giác vuông tại , ta có (định lý Pytago).
Lời giải:
Vì hai vệ tinh cùng cách mặt đất nên tam giác cân tại O.
Ta có:
Trong tam giác cân AOB ta có: nên là trung điểm của
Suy ra:
Áp dụng định lí Pytago vào tam giác vuông ta có:
Suy ra:
Suy ra:
Vì nên hai vệ tinh nhìn thấy nhau.
a)
b)
Phương pháp giải:
Áp dụng định lí Pytago vào tam giác OAB vuông tại O, ta có:
Lời giải:
a)
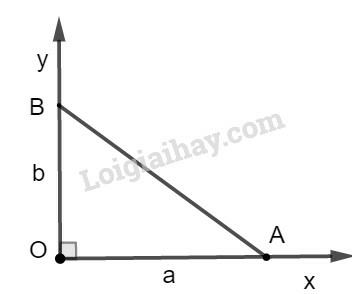
* Cách dựng:
− Dựng góc vuông .
− Trên tia , dựng đoạn .
− Trên tia , dựng đoạn .
− Nối ta có đoạn cần dựng.
* Chứng minh:
Áp dụng định lý Pytago vào tam giác vuông , ta có:
Suy ra:
b)
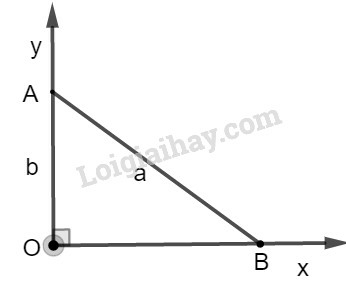
* Cách dựng :
− Dựng góc vuông .
− Trên tia , dựng đoạn .
− Dựng cung tròn tâm , bán kính bằng cắt tia tại .
Ta có đoạn cần dựng.
* Chứng minh;
Áp dụng định lí Pytago vào tam giác vuông , ta có:
Suy ra:
Cho tam giác vuông tại , đường cao .
Khi đó ta có hệ thức sau:
Từ đó suy ra cách dựng hình thỏa mãn đề bài.
Lời giải:
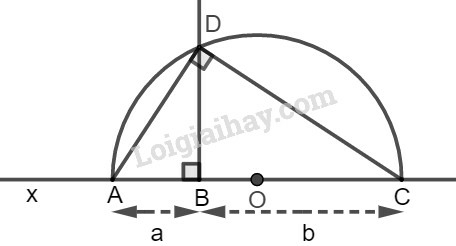
* Cách dựng:
− Dựng đường thẳng .
− Trên đường thẳng dựng liên tiếp hai đoạn thẳng , .
− Dựng nửa đường tròn tâm đường kính .
− Từ dựng đường thẳng vuông góc với cắt nửa đường tròn tâm tại .
Ta có đoạn cần dựng.
* Chứng minh:
Nối và Ta có tam giác vuông tại (do và .
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
Suy ra:
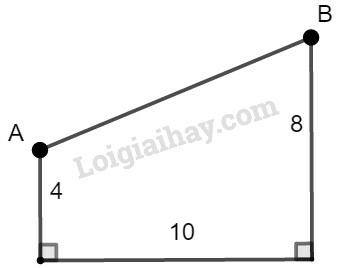
Phương pháp giải:
Áp dụng định lí Pytago: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Lời giải:
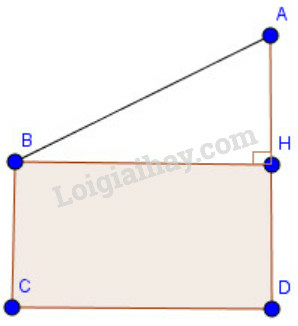
Kẻ ta được tứ giác là hình chữ nhật (vì
Suy ra và (tính chất hình chữ nhật)
Và (m)
Áp dụng định lý Pytago vào tam giác vuông , ta có:
Suy ra:
Vậy băng chuyền dài khoảng
Định lí Pytago đảo:
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh còn lại thì tam giác đó là tam giác vuông.
Lời giải:
Ta có:
Vì tam giác có ba cạnh với độ dài các cạnh thỏa mãn định lý Pytago đảo (bình phương một cạnh bằng tổng bình phương hai cạnh còn lại) nên nó là tam giác vuông.
Vậy góc đối diện với cạnh (cạnh dài nhất) là góc vuông.
Áp dụng định lí Pytago trong tam giác vuông :
Cho tam giác vuông tại thì ta có:
Áp dụng tính chất dãy tỉ số bằng nhau:
Áp dụng tính chất đường phân giác của tam giác.
Lời giải:
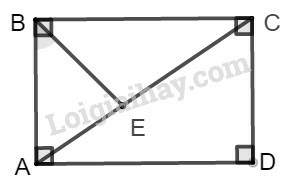
Trong tam giác , gọi giao điểm đường phân giác của góc với cạnh là .
Theo đề bài ta có:
Theo tính chất của đường phân giác, ta có:
Suy ra:
Suy ra:
Ta có
Áp dụng định lý Pytago vào tam giác vuông ABC, ta có:
Khi đó, ap dụng tính chất dãy tỉ số bằng nhau:
Suy ra:
Vậy:
Áp dụng định lí Pytago trong tam giác vuông :
Cho tam giác vuông tại thì ta có:
Áp dụng tính chất dãy tỉ số bằng nhau:
Lưu ý: Tỉ số đồng dạng của hai tam giác bằng tỉ số chu vi của hai tam giác đó.
Lời giải:
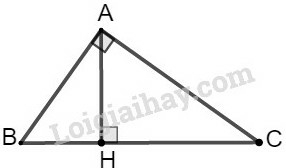
Gọi lần lượt là chu vi của các tam giác , , .
Ta có:
Xét hai tam giác vuông và , ta có:
(hai góc cùng phụ )
Vậy đồng dạng (g.g)
Suy ra:
Suy ra:
Suy ra:
Áp dụng định lí Pytago vào tam giác vuông , ta có:
Suy ra:
Xét hai tam giác vuông và , ta có:
chung
Nên đồng dạng (g.g)
Suy ra các tam giác đồng dạng với nhau nên:
Suy ra:
+ Tính chất đường phân giác:
- Đường phân giác trong của một tam giác chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn ấy.
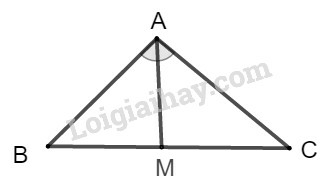
Xét tam giác ABC có AM là phân giác của góc trong .
Ta có hệ thức:
- Đường phân giác ngoài tại một đỉnh của tam giác chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn thẳng ấy.
+ Tính chất tỉ lệ thức:
Lời giải: