Bài 7 trang 69 SGK Toán 9 Tập 1 :Người ta đưa ra hai cách vẽ đoạn trung bình nhân của hai đoạn thẳng (tức là ) như trong hai hình sau:
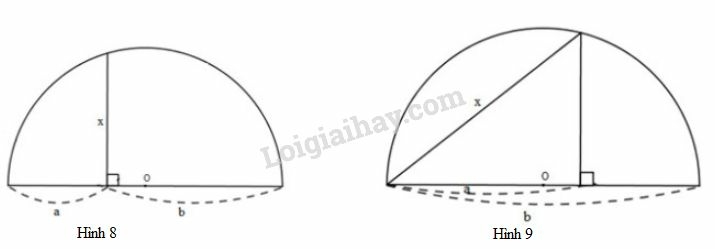
Dựa vào các hệ thức (1) và (2), hãy chứng minh các cách vẽ trên là đúng.
Gợi ý: Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác ấy là tam giác vuông.
Phương pháp giải:
+) Đặt tên các điểm và nối các điểm lại để xuất hiện tam giác.
+) Dùng dấu hiệu: "tam giác có đường trung tuyến ứng với cạnh huyền bằng nửa cạnh đó là tam giác vuông" để chứng minh tam giác vuông.
+ Dùng các hệ thức sau để chứng minh là trung bình nhân của :
+) Nêu các bước để vẽ được đoạn trung bình nhân.
Lời giải:
Cách 1: Đặt tên các đoạn thẳng như hình bên. 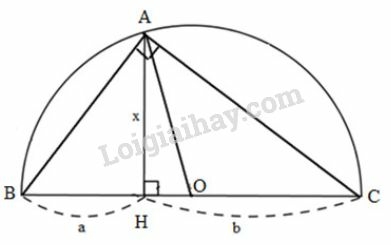
Xét có:
(cùng bằng bán kính đường tròn (O))
Mà là trung tuyến ứng với cạnh của .
Suy ra vuông tại ( tam giác có đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền thì là tam giác vuông)
Xét vuông tại , đường cao . Áp dụng hệ thức , ta được:
Vậy là trung bình nhân của và .
Cách vẽ: Bước : Đặt . Xác định trung điểm của đoạn .
Bước : Vẽ nửa đường tròn tâm bán kính .
Bước : Kẻ thẳng đi qua và vuông góc với . Đường thẳng này cắt nửa đường tròn tại .
Bước : Nối và ta được là đoạn trung bình nhân của hai đoạn thẳng .
Cách 2: Vẽ và đặt tên như hình bên dưới
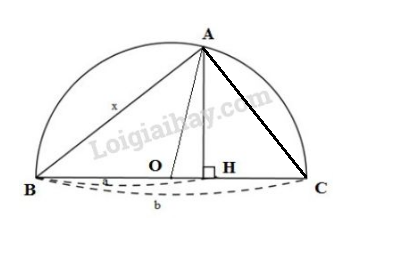
Xét có:
(cùng bằng bán kính đường tròn (O))
Mà là trung tuyến ứng với cạnh của .
Suy ra vuông tại (tam giác có đường trung tuyến ứng với cạnh huyền bẳng nửa cạnh đó thì là tam giác vuông)
Xét vuông tại , đường cao . Áp dụng hệ thức , ta có:
Vậy là trung bình nhân của và .
Cách vẽ: Bước : Đặt . Xác định trung điểm của đoạn .
Bước : Vẽ nửa đường tròn tâm bán kính .
Bước : Kẻ đường thẳng đi qua điểm và vuông góc với . Đường thẳng này cắt nửa đường tròn tại .
Bước : Nối và ta được là đoạn trung bình nhân của hai đoạn thẳng