Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là 1 và 2

Thanh Trà Ngày: 17-10-2022 Lớp 9

1.3 K

Với giải Bài 6 trang 69 Toán lớp 9 chi tiết trong Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán lớp 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông

Bài 6 trang 69 SGK Toán 9 Tập 1 :Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là

1

và

2

. Hãy tính các cạnh góc vuông của tam giác này.

Phương pháp giải:

+) Tính cạnh huyền: $a = b^{'} + c^{'}$ .

+) Dùng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền $b^{2} = b^{'} . a; c^{2} = c^{'} . a$ , biết hình chiếu $b^{'}, c^{'}$ và cạnh huyền $a$ , tính được $a, b$ .

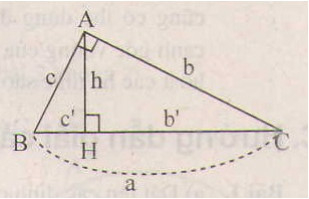
Giải Toán 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông (ảnh 21)

Lời giải:

Xét $Δ A B C$ vuông tại $A$ , đường cao $A H$ , $B H = 1, C H = 2$ . Ta cần tính $A B, A C$
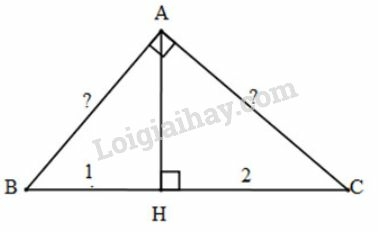
Giải Toán 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông (ảnh 22)

Cách 1:

Ta có: $B C = B H + H C = 1 + 2 = 3$

Áp dụng hệ thức lượng trong $Δ A B C$ vuông tại $A$ , đường cao $A H$ , ta có:

* $A B^{2} = B H . B C \Leftrightarrow A B^{2} = 1.3 = 3$

$\Leftrightarrow A B = \sqrt{3}$

* $A C^{2} = C H . B C \Leftrightarrow A C^{2} = 2.3 = 6$

$\Leftrightarrow A C = \sqrt{6}$

Vậy độ dài hai cạnh góc vuông cần tìm là $\sqrt{3}$ và $\sqrt{6}$ .

Cách 2:

Áp dụng hệ thức lượng trong $Δ A B C$ vuông tại $A$ , đường cao $A H$ , ta có:

$A H^{2} = B H . H C = 1.2 = 2 \Rightarrow A H = \sqrt{2}$

Áp dụng định lí Pytago trong tam giác vuông ABH, ta được:

$A B^{2} = B H^{2} + A H^{2} = 1^{2} + (\sqrt{2})^{2} = 3 \Rightarrow A B = \sqrt{3}$

Áp dụng định lí Pytago trong tam giác vuông ACH, ta được:

$A C^{2} = C H^{2} + A H^{2} = 2^{2} + (\sqrt{2})^{2} = 4 + 2 = 6 \Rightarrow A C = \sqrt{6}$ $A C^{2} = C H^{2} + A H^{2} = 2^{2} + (\sqrt{2})^{2} = 4 + 2 = 6 \Rightarrow A C = \sqrt{6}$