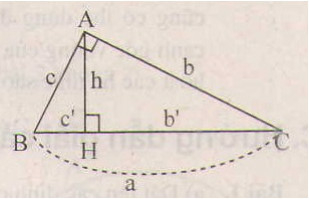
Bài 5 trang 69 SGK Toán 9 Tập 1 :Trong tam giác vuông với các cạnh góc vuông có độ dài là và , kẻ đường cao ứng với cạnh huyền. Hãy tính đường cao này và độ dài các đoạn thẳng mà nó định ra trên cạnh huyền.
Lời giải:
Xét vuông tại , đường cao có . Ta cần tính và .
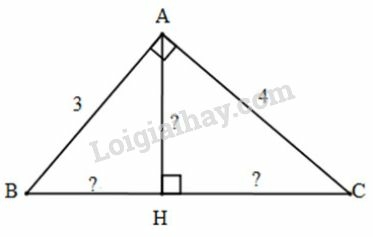
Áp dụng định lí Pytago cho vuông tại , ta có:
.
Xét vuông tại , đường cao . Áp dụng các hệ thức lượng trong tam giác vuông, ta được:
*
*
*
Phương pháp giải:
+) Dùng định lí Pytago để tính cạnh huyền.
+) Dùng hệ thức . Biết hai cạnh góc vuông và cạnh huyền tính được đường cao .
+) Biết cạnh huyền và các cạnh góc vuông . Dùng các hệ thức ; suy ra .