Xét hình 1. Chứng minh tam giác AHB đồng dạng với tam giác CHA

Thanh Trà Ngày: 17-10-2022 Lớp 9

563

Với giải Câu hỏi 1 trang 66 Toán lớp 9 chi tiết trong Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán lớp 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông

Trả lời câu hỏi 1 trang 66 SGK Toán 9 Tập 1:Xét hình 1. Chứng minh $Δ A H B \sim Δ C H A$ . Từ đó suy ra hệ thức (2) là $h^{2} = b^{'} c^{'} .$

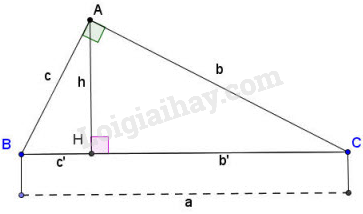
Giải Toán 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông (ảnh 1)

Hình 1

Phương pháp giải:

Sử dụng trường hợp đồng dạng góc-góc để chứng minh hai tam giác $A B H$ và $C A H$ đồng dạng.

Từ đó suy ra tỉ lệ cạnh và hệ thức cần tìm.

Lời giải:

Ta có $\hat{B A H} + \hat{C A H} = 90^{0}$ và $\hat{C A H} + \hat{A C H} = 90^{0}$ (do tam giác $A H C$ vuông tại $H$ )

Do đó $\hat{B A H} = \hat{A C H}$ (cùng phụ $\hat{C A H}$ )

Xét $Δ A B H$ và $Δ C A H$ có:

$\hat{A H B} = \hat{A H C} (= 90^{o}$ )

$\hat{B A H} = \hat{A C H}$ (chứng minh trên )

$\Rightarrow Δ A B H \sim Δ C A H (g . g)$

$\Rightarrow \frac{A H}{C H} = \frac{B H}{A H}$ ( cặp cạnh tương ứng tỉ lệ)

$\Rightarrow A H^{2} = B H h a y h^{2} = b^{'} . c^{'}$

Từ khóa :

toán 9 Giải bài tập

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Cho tam giác ABC vuông tại A có AB = 5cm, BC = 13cm. AH là đường cao Nguyễn Mạnh Tài

Toán Tổng hợp kiến thức

Cho tam giác ABC vuông tại A, đường cao AH, biết AH : AC = 3: 5 và AB = 15cm Nguyễn Mạnh Tài

Toán Tổng hợp kiến thức

Cho tam giác ABC vuông tại A, biết AB = 3cm, AC = 4cm. Hãy giải tam giác ABC Nguyễn Mạnh Tài

Toán Tổng hợp kiến thức

Cho tam giác ABC vuông tại A, biết AB = 6cm, C = 30o. Hãy giải tam giác ABC Nguyễn Mạnh Tài

Tìm kiếm