Với giải sách bài tập Toán 10 Bài tập cuối chương 5 sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:
Giải SBT Toán lớp 10 Bài tập cuối chương 5
Giải SBT Toán 10 trang 17 Tập 2
A. 3.
B. 6.
C. 5.
D. 2.
Lời giải:
Đáp án đúng là B
Việc chọn con đường đi từ nhà đến trường của bạn Thảo là thực hiện hai hành động liên tiếp: chọn một con đường đi từ nhà đến hiệu sách, sau đó chọn một con đường đi từ hiệu sách đến trường.
Bạn Thảo có 3 cách chọn một con đường đi từ nhà đến hiệu sách.
Với mỗi cách chọn một con đường đi từ nhà đến hiệu sách, bạn Thảo có 2 cách chọn một con đường đi từ hiệu sách đến trường.
Vậy theo quy tắc nhân, bạn Thảo có tất cả 3.2 = 6 cách chọn đường đi từ nhà đến trường, qua hiệu sách.
Do đó ta chọn phương án B.
A. 3.
B. 6.
C. 5.
D. 2 .
Lời giải:
Đáp án đúng là C
Nếu chọn theo hướng đi thứ nhất thì bạn Huy có 2 cách chọn một hiệu sách.
Nếu chọn theo hướng đi thứ hai thì bạn Huy có 3 cách chọn một hiệu sách.
Vậy theo quy tắc cộng, bạn Huy có tất cả 2 + 3 = 5 cách chọn một hiệu sách để đến.
Do đó ta chọn phương án C.
Bài 40 trang 17 SBT Toán 10 Tập 2: Trong các phát biểu sau, phát biểu nào sai?
A. với k, n là các số tự nhiên, 0 ≤ k ≤ n.
B. với k, n là các số tự nhiên, 1 ≤ k ≤ n.
C. Pn = n! với n là số nguyên dương.
D. (a – b)5 = a5 – 5a4b + 10a3b2 – 10a2b3 + 5ab4 – b5.
Lời giải:
Đáp án đúng là A
⦁ với k, n là các số tự nhiên, 0 ≤ k ≤ n.
Do đó phương án A sai.
⦁ với k, n là các số tự nhiên, 1 ≤ k ≤ n.
Suy ra , với k, n là các số tự nhiên, 1 ≤ k ≤ n.
Do đó phương án B đúng.
⦁ Pn = n! với n là số nguyên dương.
Do đó phương án C đúng.
⦁ Công thức khai triển nhị thức Newton của biểu thức (a – b)5 là:
(a – b)5 = a5 – 5a4b + 10a3b2 – 10a2b3 + 5ab4 – b5.
Do đó phương án D đúng.
Vậy ta chọn phương án A.
A. 1 140.
B. 60.
C. 6 840.
D. 8 000.
Lời giải:
Đáp án đúng là A
Mỗi cách chọn 3 điểm trong 20 điểm phân biệt đã cho là một tổ hợp chập 3 của 20.
Số cách chọn 3 điểm trong 20 điểm đã cho là .
Vậy ta chọn phương án A.
a) Hai học sinh được chọn khác lớp?
A. 70.
B. 1 224.
C. 34.
D. 36.
b) Hai học sinh được chọn cùng lớp?
A. 1 191.
B. 34.
C. 36.
D. 1 224.
Lời giải:
a) Nếu hai học sinh được chọn khác lớp thì tức là một học sinh được chọn thuộc lớp 11A và học sinh được chọn còn lại thuộc lớp 12A.
Chọn một học sinh thuộc lớp 11A thì có 34 cách chọn.
Chọn một học sinh thuộc lớp 12A thì có 36 cách chọn.
Theo quy tắc nhân, nếu hai học sinh được chọn khác lớp thì nhà trường có 34.36 = 1224 cách chọn.
Vậy ta chọn phương án B.
b) Nếu hai học sinh được chọn cùng lớp thì ta sẽ có hai trường hợp sau:
Trường hợp 1: Hai học sinh được chọn thuộc lớp 11A.
Mỗi cách chọn 2 học sinh trong số 34 học sinh của lớp 11A là một tổ hợp chập 2 của 34.
Số cách chọn 2 học sinh của lớp 11A là: .
Trường hợp 2: Hai học sinh được chọn thuộc lớp 12A.
Mỗi cách chọn 2 học sinh trong số 36 học sinh của lớp 12A là một tổ hợp chập 2 của 36.
Số cách chọn 2 học sinh của lớp 12A là: .
Theo quy tắc cộng, nếu hai học sinh được chọn cùng lớp thì nhà trường có 561 + 630 = 1191 cách chọn.
Vậy ta chọn phương án A.
A. 840.
B. 5 040.
C. 35.
D. 2 401.
Lời giải:
Đáp án đúng là: C
Với mỗi số có bốn chữ số được lập ra từ các chữ số 1, 2, 3, 4, 5, 6, 7 thì luôn có duy nhất 1 cách sắp xếp thỏa mãn yêu cầu bài toán.
Mỗi cách chọn một số có bốn chữ số thỏa mãn yêu cầu bài toán từ các chữ số 1, 2, 3, 4, 5, 6, 7 là một tổ hợp chập 4 của 7.
Số cách chọn một số có bốn chữ số thỏa mãn yêu cầu bài toán là: .
Vậy ta chọn phương án C.
Giải SBT Toán 10 trang 18 Tập 2
Bài 44 trang 18 SBT Toán 10 Tập 2: Khai triển các biểu thức sau:
a) (x – 2y)4;
Lời giải:
a) (x – 2y)4 = x4 + 4.x3.(–2y) + 6.x2.(–2y)2 + 4.x.(–2y)3 + (–2y)4
= x4 – 8x3y + 24x2y2 – 32xy3 + 16y4.
b) (–3x – y)5
= (–3x)5 + 5.(–3x)4.(–y) + 10.(–3x)3.(–y)2 + 10.(–3x)2.(–y)3 + 5.(–3x).(–y)4 + (–y)5.
= –243x5 – 405x4y – 270x3y2 – 90x2y3 – 15xy4 – y5.
Bài 45 trang 18 SBT Toán 10 Tập 2: Xác định hệ số của x3 trong khai triển biểu thức (5x – 1)4.
Lời giải:
Ta có: (5x – 1)4 = (5x)4 + 4.(5x)3.(– 1) + 6.(5x)2.(– 1)2 + 4.(5x).(– 1)3 + (– 1)4
= 625 – 500x3 + 150x – 20x + 1
Số hạng chứa x3 trong khai triển biểu thức (5x – 1)4 là 4.(5x)3.(–1) = –500x3.
Vậy hệ số của x3 trong khai triển biểu thức (5x – 1)4 là –500.
Bài 46 trang 18 SBT Toán 10 Tập 2: Xác định hệ số của x4 trong khai triển biểu thức (2x + 3)5.
Lời giải:
Ta có: (2x + 3)5 = (2x)5 + 5.(2x)4.3 + 10.(2x)3.32 + 10.(2x)2.33 + 5.(2x)1.34 + 35
= 32x5 + 240x4 + 720x3 + 1 080x2 + 810x + 243
Số hạng chứa x4 trong khai triển biểu thức (2x + 3)5 là 240x4.
Vậy hệ số của x4 trong khai triển biểu thức (2x + 3)5 là 240.
Lời giải:
Trường hợp 1: Lớp 10A đi thành phố M.
Mỗi cách chọn và xếp thứ tự 4 địa điểm tham quan nếu lớp 10A đi thành phố M là một chỉnh hợp chập 4 của 10.
Số cách chọn và xếp thứ tự 4 địa điểm tham quan nếu lớp 10A đi thành phố M là:
(cách lập).
Trường hợp 2: Lớp 10A đi thành phố N.
Vì thành phố N chỉ có 4 địa điểm tham quan, nên mỗi cách xếp thứ tự vị trí cho 4 địa điểm đó là một hoán vị của 4 phần tử.
Số cách xếp thứ tự 4 địa điểm tham quan là: P4 = 4! = 24 (cách xếp).
Theo quy tắc cộng, lớp 10A có tất cả 5040 + 24 = 5064 cách lập một danh sách các địa điểm để tham quan.
Lời giải:
Mỗi cách xếp 3 đội của nước X vào 3 bảng khác nhau thì có 3! = 6 cách xếp.
Xếp 6 đội còn lại vào 3 bảng A, B, C, mỗi bảng 2 đội là thực hiện ba công việc liên tiếp: Xếp 2 đội vào bảng A, sau đó xếp 2 đội vào bảng B, cuối cùng xếp 2 đội vào bảng C.
Xếp 2 đội trong 6 đội còn lại vào bảng A thì có cách xếp.
Xếp 2 đội trong 4 đội còn lại vào bảng B thì có cách xếp.
Xếp 2 đội trong 2 đội còn lại vào bảng C thì có cách xếp.
Do đó xếp 6 đội còn lại vào 3 bảng A, B, C thì có cách xếp.
Vậy số cách xếp sao cho 3 đội bóng của nước X ở 3 bảng khác nhau là: 6.90 = 540 cách xếp.
Lời giải:
Vì đề thi có số câu thông hiểu không ít hơn 2 và có đủ 3 mức độ nên xảy ra các trường hợp sau:
Trường hợp 1: Đề thi có 3 câu thông hiểu, 1 câu vận dụng thấp và 1 câu vận dụng cao.
Khi đó ta có (cách chọn đề).
Trường hợp 2: Đề thi có 2 câu thông hiểu, 2 câu vận dụng thấp và 1 câu vận dụng cao.
Khi đó ta có (cách chọn đề).
Trường hợp 3: Đề thi có 2 câu thông hiểu, 1 câu vận dụng thấp và 2 câu vận dụng cao.
Khi đó ta có (cách chọn đề).
Vậy số đề thi tốt có thể chọn được là: 22750 + 23625 + 10500 = 56875.
Lời giải:
Gọi x là số câu trả lời đúng (x > 0).
Suy ra 50 – x là số câu trả lời sai.
Số điểm được cộng khi trả lời đúng x câu là: 0,2.x.
Số điểm bị trừ khi trả lời sai 50 – x câu là: 0,1.(50 – x).
Ta có số điểm của thí sinh là 9,4.
Suy ra 0,2.x – 0,1.(50 – x) = 9,4.
Khi đó 0,2.x – 5 + 0,1.x = 9,4.
Vì vậy 0,3.x = 14,4.
Suy ra x = 48.
Do đó thí sinh làm đúng 48 câu và làm sai 2 câu thì được 9,4 điểm.
Số cách chọn 48 câu trả lời đúng trong 50 câu của đề thi thì có cách chọn.
Ở mỗi câu, số cách chọn 1 phương án trả lời đúng là: 1 cách chọn.
Ở mỗi câu, số cách chọn 1 phương án trả lời sai trong 3 phương án sai là: 3 cách chọn.
Vì mỗi câu hỏi có 1 phương án đúng và 3 phương án sai nên số khả năng đạt được 9,4 điểm ở bài thi trên là .
Xêm thêm các bài giải SBT Toán 10 Cánh diều hay, chi tiết khác:
Bài 2: Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu không ghép nhóm
Bài 3: Các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm
Lý thuyết
1. Quy tắc cộng
Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động thứ nhất có m cách thực hiện, hành động thứ hai có n cách thực hiện (các cách thực hiện của cả hai hành động là khác nhau đôi một) thì công việc đó có m + n cách hoàn thành.
Ví dụ: Một nhóm học sinh ưu tú của lớp 10A có 13 học sinh nam và 7 học sinh nữ. Giáo viên muốn chọn ra 1 bạn để đi dự đại hội dành cho học sinh của khối. Hỏi giáo viên có bao nhiêu cách để chọn học sinh đó.
Hướng dẫn giải
Để chọn 1 học sinh ta thực hiện một trong hai hành động sau:
Chọn một học sinh trong 13 học sinh nam: Có 13 cách chọn.
Chọn một học sinh trong 7 học sinh nữ: Có 7 cách chọn.
Vậy có 13 + 7 = 20 cách chọn 1 học sinh.
Vậy giáo viên có 20 cách để lựa chọn một học sinh để đi dự đại hội.
Nhận xét: Một công việc được hoàn thành bởi một trong ba hành động. Nếu hành động thứ nhất có m cách thực hiện, hành động thứ hai có n cách thực hiện, hành động thứ ba có p cách thực hiện (các cách thực hiện của cả hai hành động là khác nhau đôi một) thì công việc đó có m + n + p cách hoàn thành.
Ví dụ: Nhà trường tổ chức cho học sinh tìm hiểu về các đề tài. Ban tổ chức đưa ra ba nội dung gồm: 5 đề tài về khoa học tự nhiên, 6 đề tài xã hội và 10 đề tài về môi trường và cuộc sống. Hỏi mỗi học sinh có bao nhiêu khả năng lựa chọn. Biết mỗi học sinh chỉ được chọn một đề tài.
Hướng dẫn giải
Mỗi học sinh chọn một đề tài, tức là mỗi học sinh thực hiện một trong ba hành động sau:
Chọn một đề tài trong 5 đề tài về khoa học tự nhiên: Có 5 cách chọn.
Chọn một đề tài trong 6 đề tài về xã hội: Có 6 cách chọn.
Chọn một đề tài trong 10 đề tài về môi trường và cuộc sống: Có 10 cách chọn.
Vậy có 5 + 6 + 10 = 21 cách chọn 1 đề tài.
Vậy mỗi học sinh có 21 khả năng lựa chọn một đề tài để tìm hiểu.
2. Quy tắc nhân
Một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu hành động thứ nhất có m cách thực hiện và ứng với mỗi cách thực hiện hành động thứ nhất, có n cách thực hiện hành động thứ hai thì công việc có m.n cách hoàn thành.
Ví dụ: Để đi từ nhà An đến nhà Minh có hai con đường để đi. Từ nhà Minh đến nhà Lâm có ba con đường để đi. Hỏi có bao nhiêu cách lựa chọn con đường đi từ nhà An đến nhà Lâm và đi qua nhà Minh.
Hướng dẫn giải
Việc lựa chọn con đường đi từ nhà An đến nhà Lâm và đi qua nhà Minh là thực hiện hai hành động liên tiếp.
– Chọn con đường đi từ nhà An đến nhà Minh có 2 cách chọn;
– Chọn con đường đi từ nhà Minh đến nhà Lâm có 3 cách chọn.
Theo quy tắc nhân, ta có 2.3 = 6 cách chọn con đường đi từ nhà An đến nhà Lâm và đi qua nhà Minh.
Vậy có 6 cách chọn con đường đi từ nhà An đến nhà Lâm và đi qua nhà Minh.
Nhận xét: Một công việc được hoàn thành bởi ba hành động liên tiếp. Nếu hành động thứ nhất có m cách thực hiện và ứng với mỗi cách thực hiện hành động thứ nhất, có n cách thực hiện hành động thứ hai; ứng với mỗi cách thực hiện hành động thứ nhất và mỗi cách thực hiện hành động thứ hai có p cách thực hiện hành động thứ ba thì công việc có m.n.p cách hoàn thành.
Ví dụ: Một người ăn trưa tại một của hàng. Trong thực đơn có 5 món thịt, 3 món rau và 4 món tráng miệng. Hỏi người này có bao nhiêu cách để lựa chọn một bữa ăn gồm 1 món thịt, 1 món rau và 1 món tráng miệng.
Hướng dẫn giải
Để lựa chọn một bữa ăn có 1 món thịt, 1 món rau và 1 món tráng miệng thì phải thực hiện qua ba hành động liên tiếp là:
– Lựa chọn một món thịt: có 5 cách chọn.
– Lựa chọn một món rau: có 3 cách chọn.
– Lựa chọn một món tráng miệng: có 4 cách chọn.
Theo quy tắc nhân, ta có 5.3.4 = 60 cách chọn 1 món thịt, 1 món rau và 1 món tráng miệng.
Vậy người này có 60 cách để lựa chọn một bữa ăn gồm 1 món thịt, 1 món rau và 1 món tráng miệng.
3. Sơ đồ hình cây
Nhận xét:
– Sơ đồ hình cây (Hình 6) là sơ đồ bắt đầu tại một nút duy nhất với cách nhánh tỏa ra các nút bổ sung.
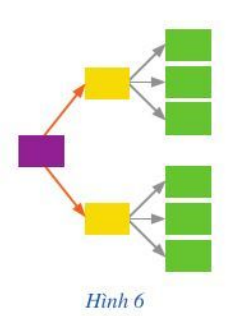
– Ta có thể sử dụng sơ đồ hình cây để đếm số cách hoàn thành một công việc khi công việc đó đòi hỏi những hành động liên tiếp.
Ví dụ: Bạn Diệp muốn mua một chiếc đồng hồ đeo tay. Biết đồng hồ có 3 loại mặt để lựa chọn: mặt vuông, mặt tròn, mặt elip; có 2 loại dây đồng hồ là: dây da màu đen, dây da màu nâu. Hỏi Diệp có bao nhiêu cách để lựa chọn một chiếc đồng hồ.
Hướng dẫn giải
Để lựa chọn một chiếc đồng hồ phải trải qua hai hành động: Lựa chọn mặt đồng đồ, sau đó ứng với mỗi cách lựa chọn mặt đồng hồ ta lại lựa chọn dây đồng hồ.
Khi đó, ta có sơ đồ hình cây mô tả các cách chọn một chiếc đồng hồ như sau:
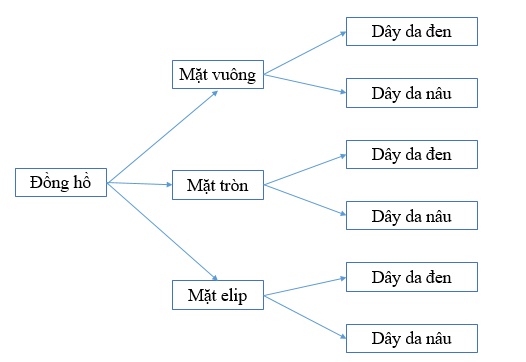
Quan sát sơ đồ hình cây ta thấy có 6 cách lựa chọn một chiếc đồng hồ.
Vậy có 6 cách để bạn Diệp lựa chọn 1 chiếc đồng hồ.
4. Vận dụng trong bài toán đếm
Việc kiểm đến có ý nghĩa quan trọng trong toán học và thực tiễn, đặc biệt trong thống kê và xác suất. Kết quả đếm cho phép chúng ta xác định số khả năng mà một sự kiện có thể xảy ra để làm cơ sở cho việc đưa ra quyết định. Quy tắc cộng, quy tắc nhân và sơ đồ hình cây là những nguyên tắc cơ bản trong các bài toán đếm.
a. Vận dụng trong giải toán
Ví dụ: Cho 3 chữ số 3; 4; 5. Lập được bao nhiêu số tự nhiên có 3 chữ số đôi một khác nhau từ ba chữ số trên.
Hướng dẫn giải
Gọi số có ba chữ số đôi một khác nhau có dạng abc.
Để được một số có ba chữ số ta phải thực hiện 3 hành động liên tiếp.
– Chọn chữ số a: ta chọn một trong 3 chữ số {3; 4; 5}, có 3 cách chọn.
– Chọn chữ số b: chữ số b phải khác chữ số a, nên chữ số b có 2 cách chọn.
– Chọn chữ số c: chữ số c phải khác chữ số a và b nên chữ số c có 1 cách chọn.
Theo quy tắc nhân, ta có 3.2.1 = 6 cách chọn.
Vậy ta lập được 6 số tự nhiên có ba chữ số đôi một khác nhau từ ba chữ số {3; 4; 5}.
b. Vận dụng trong thực tiễn
Ví dụ: Bạn Mai muốn đặt mật khẩu cho điện thoại của mình bằng các chữ số. Biết mật khẩu là dãy số gồm 6 chữ số. Hỏi bạn Mai có bao nhiêu cách để đặt mật khẩu.
Hướng dẫn giải
Gọi mật khẩu cần đặt có dạng abcfeg.
Việc chọn mật khẩu là chọn liên tiếp 6 chữ số a, b, c, d, e, g mỗi chữ số là một trong các chữ số {0; 1; 2; …; 9}.
Chọn a: là chọn 1 trong các chữ số {0; 1; 2; …; 9}. Có 10 cách chọn.
Chọn b: là chọn 1 trong các chữ số {0;1; 2; …; 9}. Có 10 cách chọn.
Chọn c: là chọn 1 trong các chữ số {0; 1; 2; …; 9}. Có 10 cách chọn.
Chọn d: là chọn 1 trong các chữ số {0; 1; 2; …; 9}. Có 10 cách chọn.
Chọn e: là chọn 1 trong các chữ số {0; 1; 2; …; 9}. Có 10 cách chọn.
Chọn g: là chọn 1 trong các chữ số {0; 1; 2; …; 9}. Có 10 cách chọn.
Theo quy tắc nhân ta có 10 .10. 10. 10. 10. 10 = 1 000 000 cách đặt mật khẩu.
Vậy Mai có 1 000 000 cách để đặt mật khẩu.
5. Hoán vị
a. Định nghĩa
Cho tập hợp A gồm n phần tử (n ∈ ℕ*).
Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập hợp A được gọi là một hoán vị của n phần tử đó.
Ví dụ: Từ 3 chữ số 3, 5, 7 có thể lập được bao nhiêu số có ba chữ số khác nhau ?
Hướng dẫn giải
Mỗi cách sắp xếp ba chữ số đã cho để lập thành một số có ba chữ số khác nhau là một hoán vị của ba chữ số đó.
Ta có các số sau : 357 ; 375 ; 537 ; 573 ; 735 ; 753.
Vậy có 6 số có ba chữ số khác nhau lập từ ba chữ số 3, 5, 7.
b. Số các hoán vị
Kí hiệu Pn là số các hoán vị của n phần tử. Ta có Pn = n . (n – 1) … 2.1
Quy ước : Tích 1.2…n được viết là n! (đọc là n giai thừa), tức là n! = 1 . 2 … n.
Như vậy Pn = n!.
Ví dụ: Có ba bạn học sinh Nam, Long, Vinh. Giáo viên muốn xếp ba bạn này vào 3 vị trí chỗ ngồi. Hỏi có bao nhiêu cách xếp.
Hướng dẫn giải
Xếp ba bạn Nam, Long, Vinh vào 3 vị trí chỗ ngồi là một hoán vị của 3 bạn.
Ta có P3 = 3! = 1.2.3 = 6.
Vậy có 6 cách xếp 3 bạn Nam, Long, Vinh vào ba vị trí chỗ ngồi.
6. Chỉnh hợp
a. Định nghĩa
Cho tập hợp A gồm n phần tử và một số nguyên k với 1 ≤ k ≤ n. Mỗi kết quả của việc lấy k phần tử từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho.
Ví dụ: Một nhóm có 10 học sinh trong đó có 3 bạn học sinh ưu tú là: Long, Hoa, Trung. Giáo viên muốn chọn ra 2 trong 3 bạn để bầu làm nhóm trưởng và nhóm phó.
Hỏi có bao nhiêu cách để chọn.
Hướng dẫn giải
Có các cách để chọn 2 bạn một bạn làm nhóm trưởng, một bạn làm nhóm phó trong ba bạn là : Long – Hoa ; Hoa – Long ; Long – Trung ; Trung – Long ; Hoa – Trung ; Trung – Hoa.
Vậy có 6 cách để chọn một học sinh nam và một học sinh nữ trong 3 bạn để làm phóm trưởng và nhóm phó.
b. Số cách chỉnh hợp
Kí hiệu là số các chỉnh hợp chập k của n phần tử (1 ≤ k ≤ n).
Ta có: = n.(n – 1)…(n – k + 1).
Ví dụ: Có 6 chữ số {1; 2; 3 ; 4 ; 5; 6}. Hỏi từ 6 chữ số trên ta lập được bao nhiêu số có 3 chữ số đôi một khác nhau.
Hướng dẫn giải
Từ 6 chữ số, ta lấy ba chữ số sau đó sắp xếp để được một số có ba chữ số khác nhau.
Khi đó, số các số tạo thành là một chỉnh hợp chập 3 của 6 chữ số.
Ta có = 6.5.4 = 120.
⇒ Có 120 số được tạo thành.
Vậy từ 6 chữ số trên ta lập được 120 số có 3 chữ số đôi một khác nhau.
7. Định nghĩa tổ hợp
Cho tập hợp A gồm n phần tử và một số nguyên k với 1 ≤ k ≤ n.
Mỗi tập con gồm k phần tử được lấy ra từ n phần tử của A được gọi là một tổ hợp chập k của n phần tử đó.
Ví dụ : Bạn Mai có 4 chiếc váy màu hồng, màu đỏ, màu trắng, màu tím. Mai muốn chọn 3 trong 4 chiếc váy để mang đi du lịch. Hãy viết các tổ hợp 3 của 4 chiếc áo váy đó.
Hướng dẫn giải
Các tổ hợp chập 3 của 4 chiếc váy là :
Hồng – đỏ – trắng ; Hồng – đỏ – tím ; Đỏ – trắng – tím ; Hồng – trắng – tím.
Vậy ta có 4 tổ hợp chập 3 của 4 chiếc váy là : Hồng – đỏ – trắng ; Hồng – đỏ – tím ; Đỏ – trắng – tím ; Hồng – trắng – tím.
8. Số các tổ hợp
Nhận xét : Một tổ hợp chập k của n phần tử nhiều gấp k! lần số tổ hợp chập k của n phần tử đó.
Kí hiệu là là số tổ hợp chập k của n phần tử với (1 ≤ k ≤ n). Ta có :
Quy ước 0! = 1 ; .
Với những quy ước trên, ta có công thức sau: (với 0 ≤ k ≤ n).
Ví dụ : Một tổ có 8 người, bạn tổ trưởng muốn cử ra 4 bạn đi tập văn nghệ. Hỏi có bao nhiêu cách chọn ?
Hướng dẫn giải
Mỗi cách chọn 4 bạn trong 8 bạn đi trực nhật là một tổ hợp chập 4 của 8.
Ta có .
Vậy có 70 cách chọn 4 trong 8 bạn đi tập văn nghệ.
9. Tính chất của các số
Ta có hai đẳng thức sau : (0 ≤ k ≤ n) và (1 ≤ k < n).
Ví dụ: Ta có : ; .
10. Nhị thức Newton
Công thức nhị thức Newton (a + b)n ứng với n = 4 ; n = 5 :
• (a + b)4 = a4 + a3b + a2b2 + ab3 + b4
= a4 + 4a3b + 6a2b2 + 4ab3 + b4.
• (a + b)5 = a5 + a4b + a3b2 + a2b3 + ab4 + b5
= a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5.
Ví dụ:
a) Khai triển (2 + x)4 ;
b) Khai triển (x – 3)5.
Hướng dẫn giải
a) Ta có :
(2 + x)4 = 24 + 23.x + 22x2 + 2.x3 + x4
= 24 + 4.23x + 6.22.x2 + 4.2.x3 + x4
= 16 + 32x + 24x2 + 8x3 + x4.
Vậy (2 + x)4 = 16 + 32x + 24x2 + 8x3 + x4.
b) Ta có :
(x – 3)5 = x5 + x4.(–3) + x3.(–3)2 + x2.(–3)3 + x.(–3)4 + (–3)5
= x5 + 5x4.(–3) + 10x3.(–3)2 + 10x2.(–3)3 + 5x.(–3)4 + (–3)5
= x5 – 15x4 + 90x3 – 270x2 + 405x – 243.
Vậy (x – 3)5 = x5 – 15x4 + 90x3 – 270x2 + 405x – 243.