Với giải sách bài tập Toán 10 Bài 1: Định lí côsin và định lí sin trong tam giác. Giá trị lượng giác của một góc từ 0° đến 180° sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 1: Định lí côsin và định lí sin trong tam giác. Giá trị lượng giác của một góc từ 0° đến 180°

Giải SBT Toán 10 trang 75 Tập 1

Bài 1 trang 75 SBT Toán 10 Tập 1: Cho 0° < α < 180°. Chọn câu trả lời đúng.

A. cosα < 0.

B. sinα > 0.

C. tanα < 0.

D. cotα > 0.

Lời giải:

Đáp án đúng là B

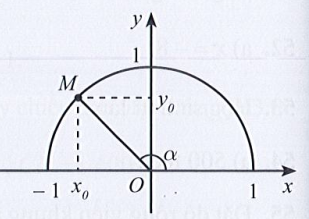
Với 0° < α < 180°, ta có:

– 1 < cosα < 1. Suy ra A sai.

0 < sinα < 1. Suy ra B đúng.

Do đó C và D sai.

Bài 2 trang 75 SBT Toán 10 Tập 1: Cho 0° < α, β < 180° và α + β = 180°. Chọn câu trả lời sai.

A. sinα + sinβ = 0.

B. cosα + cosβ = 0.

C. tanα + tanβ = 0.

D. cotα + cotβ = 0.

Lời giải:

Đáp án đúng là A

Ta có α + β = 180° nên ta có:

sinα = sinβ ⇒ sinα + sinβ = sinα + sinα = 2sinα

Vì 0° < α, β < 180° nên sinα ≠ 0.

Do đó sinα + sinβ ≠ 0. Suy ra A sai.

cosα = – cosβ ⇒ cosα + cosβ = 0. Suy ra B đúng.

tanα = – tanβ ⇒ tanα + tanβ = 0. Suy ra C đúng.

cotα = – cotβ ⇒ cotα + cotβ = 0. Suy ra D đúng.

Bài 3 trang 75 SBT Toán 10 Tập 1: Tính giá trị biểu thức T = sin²25° + sin²75° + sin²115° + sin²165°.

Lời giải:

T = sin²25° + sin²75° + sin²115° + sin²165°

= sin²25° + sin²75° + sin²75° + sin²25°

= 2sin²25° + 2sin²75°

= 2sin²25° + 2cos²25°

= 2(sin²25° + cos²25°)

= 2.1 = 2.

Bài 4 trang 75 SBT Toán 10 Tập 1: Cho tanα = – 2. Tính giá trị biểu thức P = $\frac{\text{cos}\alpha +3\sin \alpha }{\sin \alpha +3\cos \alpha }$.

Lời giải:

Ta có: tanα = – 2 thỏa mãn cosα ≠ 0

$$\begin{gathered} P=\frac{\text{cos}\alpha +3\sin \alpha }{\sin \alpha +3\cos \alpha } \\ =\frac{\frac{\text{cos}\alpha }{\text{cos}\alpha }+3\frac{\sin \alpha }{\text{cos}\alpha }}{\frac{\sin \alpha }{\text{cos}\alpha }+3\frac{\cos \alpha }{\text{cos}\alpha }} \\ =\frac{1+3\tan \alpha }{\tan \alpha +3}=\frac{1+3.\left(-2\right)}{-2+3} \\ =\frac{-5}{1}=-5 \end{gathered}$$

Vậy với tanα = – 2 thì P = – 5.

Bài 5 trang 75 SBT Toán 10 Tập 1: Cho tam giác ABC có AB = 6, AC = 8, $\widehat{A}=100°$. Tính độ dài cạnh BC và bán kính R của đường tròn ngoại tiếp tam giác (làm tròn kết quả đến hàng phần mười).

Lời giải:

Xét tam giác ABC, có:

BC² = AB² + AC² – 2.AB.AC.cosA (định lí cos)

⇔ BC² = 6² + 8² – 2.6.8.cos100°

⇔ BC² ≈ 116,7

⇔ BC ≈ 10,8.

Áp dụng định lí sin trong tam giác ABC, ta có:

$\frac{BC}{\sin A}=2R$

⇔ $\frac{10,8}{\sin 100}=2R$

⇔ $\frac{10,8}{2\sin 100°}=R$

⇔ R ≈ 5,5.

Vậy BC ≈ 10,8 và R ≈ 5,5.

Bài 6 trang 75 SBT Toán 10 Tập 1: Cho tam giác ABC có $\widehat{B}=60°,\widehat{C}=105°$ và BC = 15. Tính độ dài cạnh AC và bán kính R của đường tròn ngoại tiếp tam giác (làm tròn kết quả đến hàng đơn vị).

Lời giải:

Xét tam giác ABC, có:

$\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng ba góc)

⇒ $\widehat{A}=180°-\left(\widehat{B}+\widehat{C}\right)$$=180°-\left(60°+105°\right)=15°$

Áp dụng định lí sin trong tam giác ABC ta có:

$\frac{BC}{\sin A}=\frac{AC}{\sin B}=2R$

⇔ $\frac{15}{\sin 15}=\frac{AC}{\sin 60°}=2R$

⇒ $AC=\frac{15.\sin 60°}{\sin 15}\approx 50$

⇒ $R=\frac{15}{2.\sin 15}\approx 29.$

Vậy AC ≈ 50 và R ≈ 29.

Bài 7 trang 75 SBT Toán 10 Tập 1: Cho tam giác ABC có AB = 5, AC = 7, BC = 9. Tính số đo góc A và bán kính R của đường tròn ngoại tiếp tam giác (làm tròn kết quả đến hàng phần mười).

Lời giải:

Xét tam giác ABC, ta có:

Áp dụng hệ quả của định lí cos, ta được:

$$\begin{gathered} \cos A=\frac{A{B}^2+A{C}^2-B{C}^2}{2.AB.AC} \\ =\frac{5^2+7^2-9^2}{\mathrm{2.5.7}}=-\frac{1}{10} \end{gathered}$$

⇒ $\widehat{A}\approx$95,7°.

Ta có p = $\frac{5+7+9}{2}=10,5$

Áp dụng công thức herong, diện tích tam giác ABC là:

$$\begin{gathered} S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)} \\ =\sqrt{10,5\left(10,5-9\right)\left(10,5-7\right)\left(10,5-5\right)} \\ \approx 17,4 \end{gathered}$$

Mặt khác, ta lại có: $S=\frac{abc}{4R}$

⇒ $R=\frac{abc}{4S}=\frac{\mathrm{9.7.5}}{4.17,4}\approx 4,5$.

Vậy $\widehat{A}\approx$95,7° và R ≈ 4,5.

Bài 8 trang 75 SBT Toán 10 Tập 1: Cho hình bình hành ABCD có AB = a, BC = b, AC = m, BD = n. Chứng minh: m² + n² = 2(a² + b²).

Lời giải:

Xét tam giác ABC, có:

AC² = AB² + BC² – 2.AB.BC.cosB (định lí cos)

⇔ m² = a² + b² – 2.a.b.cosB (1)

Vì ABCD là hình bình hành nên AD = BC = b, $\widehat{A}+\widehat{B}=180°$

Vì $\widehat{A}+\widehat{B}=180°$ ⇒ cosA = – cosB ⇒ cosA + cosB = 0

Xét tam giác ABD, có:

BD² = AB² + AD² – 2.AB.AD.cosA (định lí cos)

⇔ n² = a² + b² – 2.a.b.cosA (2)

Cộng vế với vế của (1) và (2), ta được:

m² + n² = a² + b² – 2.a.b.cosB + a² + b² – 2.a.b.cosB

⇔ m² + n² = 2(a² + b²) – 2.a.b.(cosB + cosA)

⇔ m² + n² = 2(a² + b²) – 2.a.b.0

⇔ m² + n² = 2(a² + b²).

Bài 9 trang 75 SBT Toán 10 Tập 1: Từ một tấm tôn hình tròn có bán kính R = 1m, bạn Trí muốn cắt ra một hình tam giác ABC có các góc A = 45°, góc B = 75°. Hỏi bạn Trí phải cắt miếng tôn theo hai dây cung AB, BC có độ dài lần lượt bằng bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?

Lời giải:

Xét tam giác ABC, có:

$\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng ba góc)

⇒ $\widehat{C}=180°-\left(\widehat{A}+\widehat{B}\right)$$=180°-\left(45°+75°\right)=60°$

Áp dụng định lí sin trong tam giác ABC ta có:

$\frac{BC}{\sin A}=\frac{AB}{\sin C}=2R$

⇔ $\frac{BC}{\sin 45°}=\frac{AB}{\sin 60°}=2$

⇒ BC = 2.sin45° ≈ 1,41

⇒ AB = 2.sin60° ≈ 1,73

Vậy bạn Trí phải cắt miếng tôn theo hai dây cung AB,BC có độ dài lần lượt là 1,41m và 1,73m.

Bài 10 trang 75 SBT Toán 10 Tập 1: Một cây cao bị nghiêng so với mặt đất một góc 78°. Từ vị trí C cách gốc cây 20m, người ta tiến hành đo đạc và thu được kết quả $\widehat{ACB}=50°$với B là vị trí ngọn cây (Hình 10). Tính khoảng cách từ gốc cây (điểm A) đến ngọn cây (điểm B) (làm tròn kết quả đến hàng phần mười theo đơn vị mét).

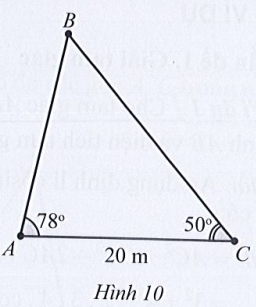
Lời giải:

Xét tam giác ABC, có:

$\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng ba góc)

⇒ $\widehat{B}=180°-\left(\widehat{A}+\widehat{C}\right)$$=180°-\left(78°+50°\right)=52°$

Áp dụng định lí sin trong tam giác ABC ta có:

$\frac{AC}{\sin B}=\frac{AB}{\sin C}$

⇔ $\frac{20}{\sin 52°}=\frac{AB}{\sin 50°}$

⇔ $AB=\frac{20.\sin 50°}{\sin 52°}\approx 19,4$.

Vậy khoảng cách từ gốc cây (điểm A) đến ngọn cây (điểm B) là 19,4 m.

Bài 11 trang 75 SBT Toán 10 Tập 1: Tàu A cách cảng C một khoảng 3km và lệch hướng bắc 1 góc 47,45°. Tàu B cách cảng C một khoảng 5km và lệch hướng bắc một góc 112,90° (Hình 11). Khoảng cách giữa hai tàu là bao nhiêu ki – lô – mét (làm tròn kết quả đến hàng phần trăm).

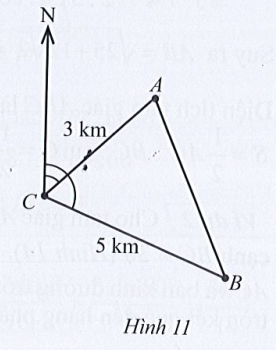
Lời giải:

Theo đầu bài, ta có: $\widehat{NCA}=47,45°$ và $\widehat{NCB}=112,9°$

$$\begin{gathered} \Rightarrow \widehat{ACB}=\widehat{NCB}-\widehat{NCA} \\ =112,90°-47,45°=65,45° \end{gathered}$$

Xét tam giác ABC, có:

AB² = AC² + BC² – 2.AC.BC.cos$\widehat{ACB}$

⇔ AB² = 3² + 5² – 2.3.5.cos65,45°

⇔ AB² ≈ 21,54

⇔ AB ≈ 4,64

Vậy khoảng cách giữa hai tàu là 4,64 km.

Xem thêm các bài giải SBT Toán 10 Cánh diều hay, chi tiết khác:

Bài ôn tập chương 3

Bài 2: Giải tam giác. Tính diện tích tam giác

Bài 3: Khái niệm vectơ

Bài 4: Tổng và hiệu của hai vectơ

Lý thuyết Giá trị lượng giác của một góc từ 0° đến 180°. Định lí côsin và định lí sin trong tam giác

1. Giá trị lượng giác của một góc từ 0° đến 180°

1.1 Định nghĩa

       

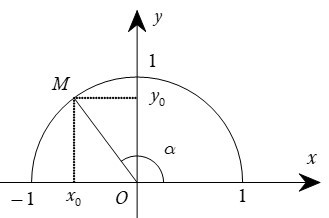
Với mỗi góc α (0 ≤ α ≤ 180°) ta xác định một điểm M (x₀, y₀) trên nửa đường tròn đơn vị sao cho góc $\widehat{\mathrm{xOM}}$= α. Khi đó ta có định nghĩa:

+) sin của góc α, kí hiệu là sinα, được xác định bởi: sinα = y₀;

+) côsin của góc α, kí hiệu là cosα, được xác định bởi: cosα = x₀;

+) tang của góc α, kí hiệu là tanα, được xác định bởi: tanα = $\frac{{\mathrm{y}}_0}{{\mathrm{x}}_0}$(x₀ ≠ 0);

+) côtang của góc α, kí hiệu là cotα, được xác định bởi: cotα = $\frac{{\mathrm{x}}_0}{{\mathrm{y}}_0}$(y₀ ≠ 0).

Các số sinα, cosα, tanα, cotα được gọi là các giá trị lượng giác của góc α.

Chú ý:

tanα = $\frac{\mathrm{sin\alpha }}{\mathrm{cos\alpha }}$(α ≠ 90°);

cotα = $\frac{\mathrm{cos\alpha }}{\mathrm{sin\alpha }}$(0 < α < 180°).

sin(90° – α) = cosα (0° ≤ α ≤ 90°);

cos(90° – α) = sinα (0° ≤ α ≤ 90°);

tan(90° – α) = cotα (0° ≤ α ≤ 90°);

cot(90° – α) = tanα (0° ≤ α ≤ 90°).

1.2. Tính chất

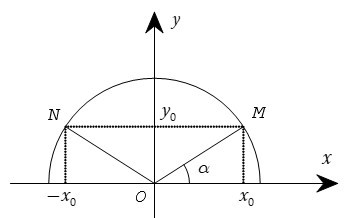
Trên hình bên ta có dây cung NM song song với trục Ox và nếu $\widehat{\mathrm{xOM}}$ = α thì $\widehat{\mathrm{xON}}$ = 180^o – α. Với 0° ≤ α ≤ 180° thì:

sin(180° – α) = sinα,

cos(180° – α) = – cosα,

tan(180° – α) = – tanα (α ≠ 90°),

cot(180° – α) = – cotα (α ≠ 0°, α ≠ 180°).

Ví dụ: Tính giá trị của biểu thức sau:

A = cos0° + cos20° + cos 40° + ... + cos160° + cos180°.

Hướng dẫn giải:

A = cos0° + cos20° + cos 40° + ... + cos160° + cos180°

        = cos0° + cos180° + cos20° + cos160° + ... + cos80° + cos100°

        = cos0° – cos0° + cos20° – cos20° + ... + cos80° – cos80°

        = 0.

1.3. Giá trị lượng giác của các góc đặc biệt

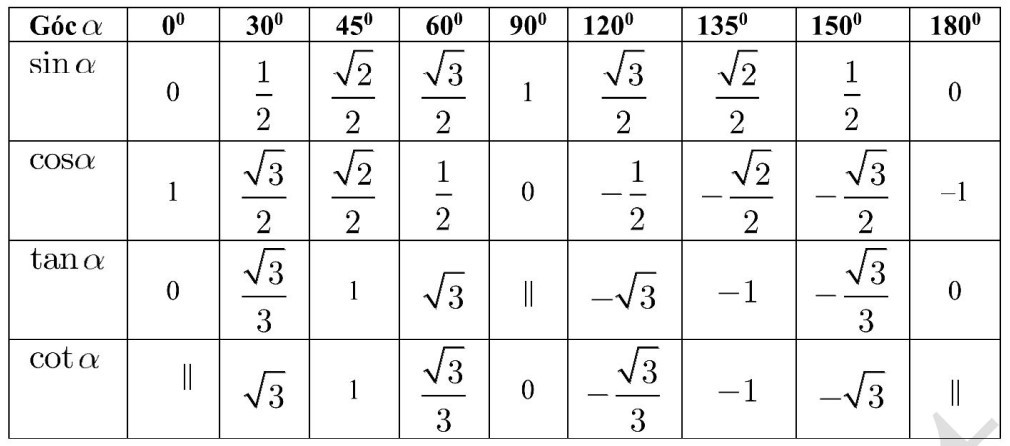
Chú thích: Dấu “||” biểu thị sự không xác định của giá trị lượng giác tại góc đó.

Ví dụ:

sin30ׄ° = $\frac{1}{2}$;

cos120° = –$\frac{1}{2}$;

tan60° = $\sqrt{6}$;

cot120° = –$\frac{\sqrt{3}}{3}$.

Chú ý: Cách sử dụng máy tính cầm tay để tính giá trị lượng giác:

– Ta có thể tìm giá trị lượng giác (đúng hoặc gần đúng) của một góc từ 0° đến 180° bằng cách sử dụng các phím: sin, cos, tan trên máy tính cầm tay.

Ví dụ: Dùng máy tính cầm tay, tính các giá trị lượng giác sau (làm tròn đến hàng phần chục nghìn).

sin55°, cos140°, tan80°.

Hướng dẫn giải:

Để tính các giá trị lượng giác trên, sau khi đưa máy tính về chế độ “độ” ta làm như sau:

	Nút ấn	Kết quả (đã làm tròn)
sin55°	sin ⇒ 5 ⇒ 5 ⇒ =	0,8192
cos140°	cos ⇒ 1 ⇒ 4 ⇒ 0 ⇒ =	–0,7660
tan80°	tan ⇒ 8 ⇒ 0 ⇒ =	5,6713

– Ta có thể tìm số đo (đúng hoặc gần đúng) của một góc từ 0° đến 180° khi biết giá trị lượng giác của góc đó bằng cách sử dụng các phím: SHIFT cùng với sin; cos; tan trên máy tính cầm tay.

Ví dụ: Sử dụng máy tính cầm tay, tìm số đo góc của α (từ 0° đến 180°) và làm tròn đến độ, biết:

a) sinα = 0,56

b) cosα = – 0,95

c) tanα = 0, 42

Hướng dẫn giải:

Để tính gần đúng số đo góc α trong mỗi trường hợp trên, sau khi đưa máy tính về chế độ “độ”, ta làm như sau:

	Nút ấn	Kết quả (đã làm tròn)
sinα = 0,56	SHIFT ⇒ sin ⇒ 0,56 ⇒ =	34°
cosα = – 0,95	SHIFT ⇒ cos ⇒ –0.95 ⇒ =	162°
tanα = 0, 42	SHIFT ⇒ tan ⇒ 0.42 ⇒ =	23°

2. Định lí côsin

Cho tam giác ABC có BC = a, CA = b, AB = c. Khi đó:

a² = b² + c² – 2bccosA,

b² = c² + a² – 2cacosB,

c² = a² + b² – 2abcosC.

Lưu ý:

cosA = $\frac{{\mathrm{b}}^2+{\mathrm{c}}^2-{\mathrm{a}}^2}{2\mathrm{bc}}$,

cosB = $\frac{{\mathrm{c}}^2+{\mathrm{a}}^2-{\mathrm{b}}^2}{2\mathrm{ca}}$,

cosC = $\frac{{\mathrm{a}}^2+{\mathrm{b}}^2-{\mathrm{c}}^2}{2\mathrm{ab}}$.

Ví dụ: Chứng minh a² = b² + c² – 2bccosA.

Hướng dẫn giải:

Cho tam giác ABC với BC = a, AC = b, AB = c. 

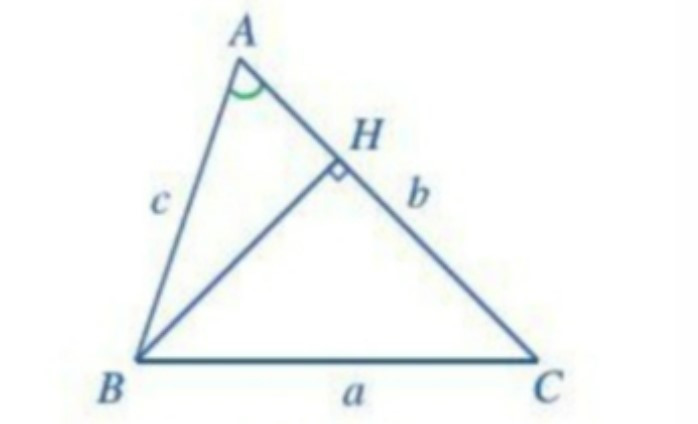
Cho tam giác ABC, đặt AB = c, AC = b, BC = a, cosA = cosα

Kẻ BH vuông góc với AC.

Xét các tam giác vuông BHC và AHB, áp dụng định lý Py–ta–go ta có:

BC² = BH² + HC²

       = BH² + (AC – AH)²

       = BH² + AC² – 2.AC.AH + AH²

       = (BH² + AH²) + AC² – 2.AC.AH

       = AB² + AC² – 2.AC.AH

 (BH² + AH² = AB² do áp dụng định lí Py–ta–go trong tam giác vuông AHB).

Xét tam giác vuông AHB, ta lại có:

cosA = $\frac{\mathrm{AH}}{\mathrm{AB}}$

⇒ AH = AB.cosA = c.cosα

Do đó: a² = BC² = AB² + AC² – 2.AC.AH

                    = c² + b² –2b. c.cosα

                       = b² + c² –2bc.cosα (đpcm).

Ví dụ: Cho tam giác ABC có $\widehat{\mathrm{A}}$ = 60°, AB = 6, AC = 8. Tính BC.

Hướng dẫn giải:

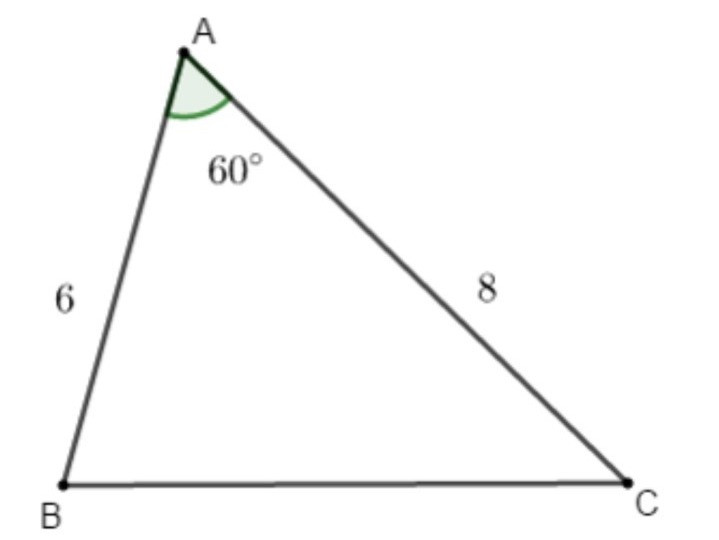
Áp dụng định lí Cosin trong tam giác ABC ta có:

BC² = AB² + AC² – 2AB.AC.cosA

Thay số ta có:

BC² = 6² + 8² – 2.6.8.cos60°

⇔ BC² = 36 + 64 – 48 = 52

⇔ BC = $\sqrt{52}$ = $2\sqrt{13}$

Vậy BC = $2\sqrt{13}$.

3. Định lí sin

Cho tam giác ABC có BC = a, CA = b, AB = c và bán kính đường tròn ngoại tiếp là R. Khi đó:

$\frac{\mathrm{a}}{\mathrm{sinA}}=\frac{\mathrm{b}}{\mathrm{sinB}}=\frac{\mathrm{c}}{\mathrm{sinC}}=2\mathrm{R}$

Lưu ý:

a = 2RsinA,

b = 2RsinB,

c = 2RsinC.

Ví dụ: Chứng minh định lí sin.

Hướng dẫn giải:

Ta chỉ cần chứng minh $\frac{\mathrm{a}}{\mathrm{sinA}}=2\mathrm{R}$, các dấu bằng kia chứng minh hoàn toàn tương tự. Ta xét ba trường hợp sau:

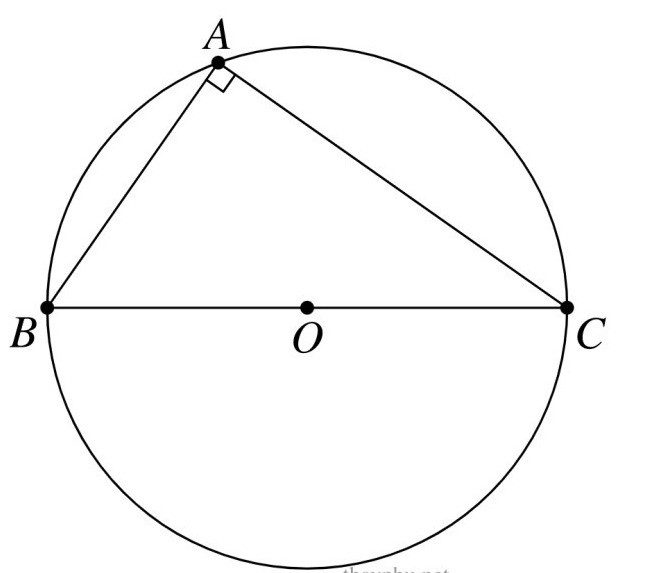
TH1: Tam giác ABC vuông tại A. Khi đó sinA = sin90° = 1. Vì BC là đường kính của đường trong ngoại tiếp tam giác ABC nên a = BC = 2R.

Vậy $\frac{\mathrm{a}}{\mathrm{sinA}}=\frac{\mathrm{BC}}{1}=2\mathrm{R}$.

                         

TH2: Góc A nhọn. Gọi D là điểm sao cho BD là đường kính. Tứ giác ABCD nội tiếp đường tròn nên $\widehat{\mathrm{A}}$ = $\widehat{\mathrm{D}}$.

Từ đó sinA = sinD = $\frac{\mathrm{BC}}{\mathrm{BD}}$ = $\frac{\mathrm{a}}{2\mathrm{R}}$.

Suy ra $\frac{\mathrm{a}}{\mathrm{sinA}}=2\mathrm{R}$.

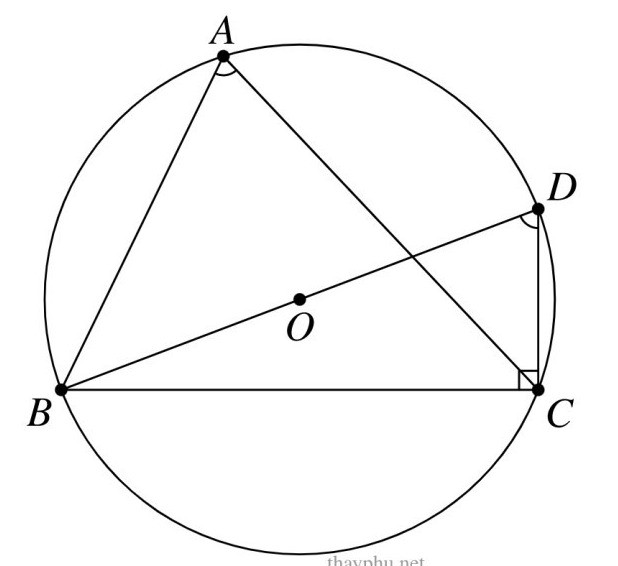
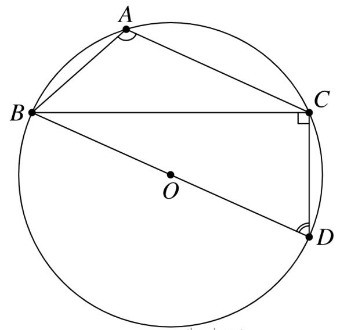
TH3: Góc $\widehat{\mathrm{A}}$ tù. Gọi D là điểm sao cho BD là đường kính. Tứ giác ABCD nội tiếp đường tròn nên $\widehat{\mathrm{A}}$+ $\widehat{\mathrm{D}}$ = 180°. Suy ra sinA = sinD ( hai góc bù nhau có sin bằng nhau).

Ta có sinD = $\frac{\mathrm{BC}}{\mathrm{BD}}$= $\frac{\mathrm{a}}{2\mathrm{R}}$

Suy ra $\frac{\mathrm{a}}{\mathrm{sinA}}=2\mathrm{R}$.

      

Ví dụ: Một người quan sát đỉnh của một ngọn núi từ hai vị trí khác nhau của tòa nhà. Lần đầu tiên người đó quan sát đỉnh núi từ tầng trệt với phương nhìn tạo với phương nằm ngang một góc 35° và lần thứ hai người này quan sát tại sân thượng của cùng tòa nhà đó với phương nhìn tạo với phương nằm ngang một góc 15°. Tính chiều cao ngọn núi đó so với mặt đất biết rằng tòa nhà cao 60 m.

Hướng dẫn giải:

Bài toán trên được mô phỏng lại như hình vẽ với A là vị trí của người đó tại sân thượng của tòa nhà, B là vị trí của người đó tại tầng trệt. C và D lần lượt là đỉnh và chân của ngọn núi.

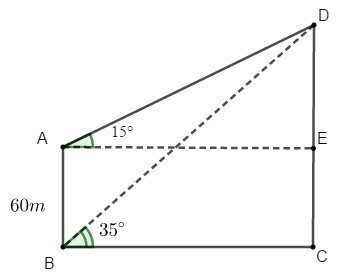
Từ A hạ AE vuông góc với CD tại E.

Theo đề ra ta có $\left\{\begin{array}{c}\mathrm{AB}=60\mathrm{m}\\ \widehat{\mathrm{DBC}}=35°\\ \widehat{\mathrm{DAE}}=15°\end{array}\right.$

Ta có:

$\widehat{\mathrm{ABD}}$ = $\widehat{\mathrm{ABC}}$ – $\widehat{\mathrm{DBC}}$= 90° – 35° = 55°;

$\widehat{\mathrm{BAD}}$ = $\widehat{\mathrm{BAE}}$+ $\widehat{\mathrm{DAE}}$ = 90° + 15° = 105°.

Mà $\widehat{\mathrm{ADB}}+\widehat{\mathrm{BAD}}+\widehat{\mathrm{ABD}}=180°$(Tổng 3 góc của một tam giác bằng 180°)

Suy ra:

$\widehat{\mathrm{ADB}}=180°-\widehat{\mathrm{BAD}}-\widehat{\mathrm{ABD}}$

          = 180° – 105° – 55°

          = 20°

Áp dụng định lí sin trong tam giác ABD ta có:

$\frac{\mathrm{AB}}{\sin \widehat{\mathrm{ADB}}}=\frac{\mathrm{BD}}{\sin \widehat{\mathrm{BAD}}}$

⇔ BD = $\frac{\mathrm{AB}.\sin \widehat{\mathrm{BAD}}}{\sin \widehat{\mathrm{ADB}}}$= $\frac{60.\sin 105°}{\sin 20°}$≈ 169,45 (m).

Xét tam giác CBD vuông tại C, ta có: