Với lời giải SBT Toán 10 trang 100 Tập 2 chi tiết trong Bài 2: Xác suất của biến cố sách Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 2: Xác suất của biến cố

Bài 1 trang 100 SBT Toán 10 Tập 2: Gieo một con xúc xắc 4 mặt cân đối và đồng chất ba lần. Tính xác suất của các biến cố:

a) “Tổng các số xuất hiện ở đỉnh phía trên của con xúc xắc trong ba lần gieo lớn hơn 2”;

b) “Có đúng một lần số xuất hiện ở đỉnh phía trên của con xúc xắc là 2”.

Lời giải:

a) Biến cố “Tổng các số xuất hiện ở đỉnh phía trên của con xúc xắc trong ba lần gieo lớn hơn 2” đây là biến cố chắc chắn nên ta có P(A) = 1.

b) Số phần tử của không gian mẫu n(Ω) = 4³ = 64

Gọi B là biến cố: “Có đúng một lần số xuất hiện ở đỉnh phía trên của con xúc xắc là 2”

Trường hợp 1. Lần thứ nhất số xuất hiện ở đỉnh phía trên của con xúc xắc là 2

Vì có đúng một lần số xuất hiện ở đỉnh phía trên của con xúc xắc là 2 nên số xuất hiện ở hai lần sau phải khác 2 nên mỗi lần có 3 kết quả sảy ra

Ta có 1.3² = 9 kết quả thuận lợi

Trường hợp 2. Lần thứ hai số xuất hiện ở đỉnh phía trên của con xúc xắc là 2

Tương tự trường hợp 1 có 1.3² = 9 kết quả thuận lợi

Trường hợp 3. Lần thứ ba số xuất hiện ở đỉnh phía trên của con xúc xắc là 2

Tương tự trường hợp 1 có 1.3² = 9 kết quả thuận lợi

Số phần tử của biến cố B là: n(B) = 9 + 9 + 9 = 27

Xác suất của biến cố B là: P(B) =  $\frac{27}{64}$

Bài 2 trang 100 SBT Toán 10 Tập 2: Tung một đồng xu cân đối và đồng chất bốn lần. Tính xác suất của các biến cố:

a) “Cả bốn lần đều xuất hiện mặt giống nhau”;

b) “Có đúng một lần xuất hiện mặt sấp, ba lần xuất hiện mặt ngửa”.

Lời giải:

Số phần tử của không gian mẫu n(Ω) = 2⁴ = 16

a) Gọi A là biến cố: “Cả bốn lần đều xuất hiện mặt giống nhau”

A = {SSSS; NNNN}

Số phần tử của biến cố A là: n(A) = 2

Xác suất của biến cố A là: P(A) = $\frac{2}{16}=\frac{1}{8}$ .

b) Gọi B là biến cố: “Có đúng một lần xuất hiện mặt sấp, ba lần xuất hiện mặt ngửa”

B = {SNNN; NSNN; NNSN; NNNS}

Số phần tử của biến cố B là: n(B) = 4.

Xác suất của biến cố B là: P(B) = $\frac{4}{16}=\frac{1}{4}$ .

Bài 3 trang 100 SBT Toán 10 Tập 2: Chi có 1 cái ô xanh, 1 cái ô trắng; 1 cái mũ xanh, l cải mũ trắng, 1 cái mũ đen; 1 đôi giày đen, 1 đôi giày trắng. Chi chọn ngẫu nhiên 1 cái ô, l cái mũ và l đôi giày để đến trường.

a) Hãy vẽ sơ đồ cây mô tả các kết quả có thể xảy ra.

b) Tính xác suất của biến cố “Chỉ có 1 trong 3 thứ đồ Chi chọn có màu trắng”.

Lời giải:

a) Sơ đồ cây mô tả các kết quả có thể xảy ra

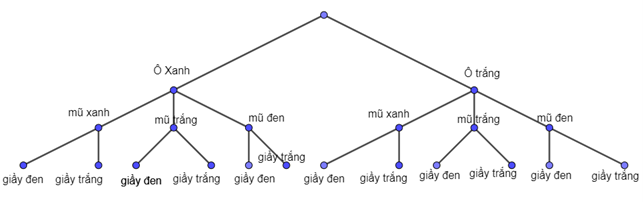
b) Số phần tử của không gian mẫu n(Ω) = 2.3.2 = 12

Gọi B là biến cố: “Chỉ có 1 trong 3 thứ đồ Chi chọn có màu trắng”

Trường hợp 1. Chi  chọn ô trắng

Chi có 2 cách chọn mũ và 1 cách chọn giày.

Do đó có 1.2.1 = 2 kết quả thuận lợi

Trường hợp 2. Chi chọn mũ trắng

Chi có 1 cách chọn ô và 1 cách chọn giầy.

Do đó có 1.1.1 = 1 kết quả thuận lợi

Trường hợp 3. Chi chọn giày trắng

Chi có 2 cách chọn mũ và 1 cách chọn ô.

Do đó có 1.2.1 = 2 kết quả thuận lợi

Số phần tử của biến cố B là: n(B) = 2 + 1 + 2 = 5

Xác suất của biến cố B là: P(B) = $\frac{5}{12}$ .

Bài 4 trang 100 SBT Toán 10 Tập 2: Chọn ngẫu nhiên 10 số tự nhiên từ dãy các số tự nhiên từ 1 đến 100. Xác định biến cố đối của các biến cố sau:

A: “Có ít nhất 3 số lẻ trong 10 số được chọn”;

B: “Tất cả 10 số được chọn đều là số chẵn”;

C: “Có không quá 5 số chẵn trong 10 số được chọn”.

Lời giải:

Biến cố đối của biến cố A là: $\overline{A}$ : “Có nhiều nhất 2 số lẻ được chọn”.

Biến cố đối của biến cố B là: $\overline{B}$ : “Có ít nhất 1 số lẻ được chọn”.

Biến cố đối của biến cố C là: $\overline{C}$ : “Có ít nhất 6 số chẵn trong 10 số được chọn”

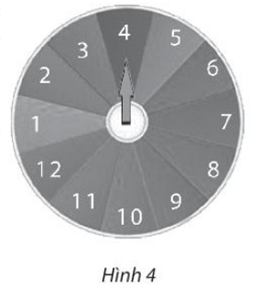
Bài 5 trang 100 SBT Toán 10 Tập 2: Trên tường có một đĩa hình tròn có cấu tạo đồng chất và cân đối. Mặt đĩa được chia thành 12 hình quạt bằng nhau và được đánh số từ 1 đến 12. Trọng quay đĩa quanh trục gắn ở tâm 3 lần và quan sát xem mỗi khi dừng lại mũi tên chỉ vào ô ghi số mấy. Tĩnh xác suất của các biến cố:

A: “Cả 3 lần mũi tên đều chỉ vào ô ghi số lẻ”;

B: “Có đúng 2 lần mũi tên chỉ vào ô ghi số lẻ”;

C: “Tích 3 số mũi tên chỉ vào là số nguyên tố ”.

Lời giải:

Số phần tử của không gian mẫu n(Ω) = 12³ = 1728

A “Cả 3 lần mũi tên đều chỉ vào ô ghi số lẻ”

Mỗi một lần quay có 6 kết quả có thể xảy ra nên số phần tử của biến cố A là: n(A) = 6³ = 216.

Xác suất của biến cố A là: P(A) = $\frac{216}{1728}=\frac{1}{8}$ .

B: “Có đúng 2 lần mũi tên chỉ vào ô ghi số lẻ”;

Vì có đúng hai lần mũi tên chỉ vào ô ghi số lẻ nên có các trường hợp

Trường hợp 1. Lần thứ nhất và lần thứ 2 mủi tên chỉ vào ô ghi số lẻ

Ta có 6 số lẻ và 6 số chẵn nên kết quả thuận lợi cho biến cố là: 6³ =  216 kết quả

Trường hợp 2. Lần thứ nhất và lần thứ 3 mủi tên chỉ vào ô ghi số lẻ

Ta có 6 số lẻ và 6 số chẵn nên kết quả thuận lợi cho biến cố là: 6³ =  216 kết quả

Trường hợp 3. Lần thứ 2 và lần thứ 3 mủi tên chỉ vào ô ghi số lẻ

Ta có 6 số lẻ và 6 số chẵn nên kết quả thuận lợi cho biến cố là: 6³ =  216 kết quả

Số phần tử của biến cố B là: n(B) = 216.3 = 648

Xác suất của biến cố B là: P(B) =  $\frac{648}{1728}=\frac{3}{8}$

C: “Tích 3 số mũi tên chỉ vào là số nguyên tố ”

Để tích 3 số là số nguyên tố thì có 2 lần mũi tên chỉ vào số 1 và 1 lần chỉ vào ô ghi số nguyên tố. Có 5 số nguyên tố gồm: 2; 3; 5; 7; 11.

Có 3 trường hợp có thể sảy ra là: Lần thứ nhất và lần thứ 2 chỉ vào ô ghi số 1; lần thứ nhất và lần thứ 3 chỉ vào ô ghi số 1; lần thứ 2 và lần thứ 3 chỉ vào ô ghi số 1.

Số phần tử của biến cố C là: n(C) = 3.1.5 = 15

Xác suất của biến cố C là: P(C) = $\frac{15}{1728}=\frac{5}{576}$ .

Xem thêm các bài giải sách bài tập Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Giải SBT Toán 10 trang 101 Tập 2

Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 4: Ba đường conic trong mặt phẳng tọa độ

Bài tập cuối chương 9

Bài 1: Không gian mẫu và biến cố

Bài 2: Xác suất của biến cố

Bài tập cuối chương 10