Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 10 Bài 2: Xác suất của biến cố chi tiết sách Toán 10 Tập 2 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài 2: Xác suất của biến cố

Giải toán lớp 10 trang 81 Tập 2 Chân trời sáng tạo

Khởi động trang 81 Toán lớp 10 Tập 2: Lấy ra ngẫu nhiên đồng thời 2 viên bi từ một hộp có chứa 5 bi xanh và 5 bi đỏ có cùng kích thước và trọng lượng. Biến cố lấy được 2 viên bi cùng màu hay 2 viên bi khác màu có khả năng xảy ra cao hơn? Trong bài này ta sẽ tìm hiểu công thức tính xác suất để có thể so sánh được khả năng xảy ra của hai biến cố trên.

Lời giải:

Để so sánh được khả năng xảy ra của hai biến cố trên ta cần tính được xác suất xảy ra từng biến cố.

1. Xác suất của biến cố

Khám phá 1 trang 81 Toán lớp 10 Tập 2: Gieo một con xúc xắc cân đối và đồng chất. Hãy so sánh khả năng xảy ra của hai biến cố:

A: “Mặt xuất hiện có số chấm là số chẵn”;

B: “Mặt xuất hiện có số chấm là số lẻ”.

Lời giải:

Do con xúc xắc được chế tạo cân đối và đồng chất nên các mặt của nó đều có cùng khả năng xuất hiện.

Không gian mẫu của phép thử trên là: Ω = {1; 2; 3; 4; 5; 6}. Có 6 kết quả không gian mẫu.

Các kết quả thuận lợi cho biến cố A là: A = {2; 4; 6}. Có 3 kết quả xảy ra biến cố A.

Các kết quả thuận lợi cho biến cố B là: B = {1; 3; 5}. Có 3 kết quả xảy ra biến cố B.

Như vậy ta thấy khả năng xảy ra của hai biến cố là bằng nhau.

Giải toán lớp 10 trang 82 Tập 2 Chân trời sáng tạo

Thực hành 1 trang 82 Toán lớp 10 Tập 2: Gieo hai con xúc xắc cân đối và đồng chất. Tính xác suất của các biến cố:

a) “Hai mặt xuất hiện có cùng số chấm”;

b) “Tổng số chấm trên hai mặt xuất hiện bằng 9”.

Lời giải:

Do hai con xúc xắc được chế tạo cân đối và đồng chất nên các mặt của nó đều có cùng khả năng xuất hiện.

Không gian mẫu của phép thử trên là:

$\Omega$ = {(1; 1); (1; 2); (1; 3); (1; 4); (1; 5); (1; 6); (2; 1); (2; 2); (2; 3); (2; 4); (2; 5); (2; 6); (3; 1); (3; 2); (3; 3); (3; 4); (3; 5); (3; 6); (4; 1); (4; 2); (4; 3); (4; 4); (4; 5); (4; 6); (5; 1); (5; 2); (5; 3); (5; 4); (5; 5); (5; 6); {(6; 1); (6; 2); (6; 3); (6; 4); (6; 5); (6; 6)}. Có 36 kết quả không gian mẫu, tức là n($\Omega$) = 36.

a) Đặt biến cố A: “Hai mặt xuất hiện có cùng số chấm”.

Khi đó A = {(1; 1); (2; 2); (3; 3); (4; 4); (5; 5); (6; 6)}.

Số kết quả thuận lợi cho A là n(A) = 6.

Do đó, xác suất của biến cố A là:

P(A) = $\frac{6}{36}=\frac{1}{6}$.

b) Đặt biến cố B: “Tổng số chấm trên hai mặt xuất hiện bằng 9”

Khi đó B = {(3; 6); (4; 5); (5; 4); (6; 3)}.

Số kết quả thuận lợi cho B là n(B) = 4.

Do đó, xác suất của biến cố B là:

P(B) = $\frac{4}{36}=\frac{1}{9}$.

Giải toán lớp 10 trang 83 Tập 2 Chân trời sáng tạo

Vận dụng trang 83 Toán lớp 10 Tập 2: Hãy tính xác suất của hai biến cố được nêu ra ở hoạt động khởi động của bài học.

Lời giải:

Đang biên soạn

2. Tính xác suất bằng sơ đồ hình cây

Thực hành 2 trang 83 Toán lớp 10 Tập 2: Ba bạn Lan, Mai và Đào đặt thẻ học sinh của mình vào một hộp kín, sau đó mỗi bạn lấy ngẫu nhiên một thẻ từ hộp. Tính xác suất của biến cố “Không bạn nào lấy đúng thẻ của mình”.

Lời giải:

Gọi thẻ của ban bạn Lan, Mai và Đào lần lượt là thẻ L, M và Đ và A là biến cố “Không bạn nào lấy đúng thẻ của mình”.

Theo sơ đồ ta có:

Có tất cả 9 kết quả có thể xảy ra nên n($\Omega$) = 6.

Trong đó có 6 kết quả thuận lợi cho A nên n(A) = 2.

Khi đó xác suất xảy ra biến cố A là: P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{2}{6}=\frac{1}{3}$.

Vậy xác suất của biến cố “Không bạn nào lấy đúng thẻ của mình” là $\frac{1}{3}$.

3. Biến cố đối

Giải toán lớp 10 trang 84 Tập 2 Chân trời sáng tạo

Khám phá 2 trang 84 Toán lớp 10 Tập 2: Một hộp có 10 tấm thẻ giống nhau được đánh số lần lượt từ 1 đến 10. Chọn ra ngẫu nhiên cùng một lúc 3 thẻ. Tính xác suất của biến cố tích các số ghi trên 3 thẻ đó là số chẵn.

Lời giải:

Số kết quả chọn ngẫu nhiên 3 thẻ từ 10 thẻ là: $C_{10}^3$.

Do đó n($\Omega$) = $C_{10}^3$ = 120.

Gọi A là biến cố: “Tích các số ghi trên 3 thẻ đó là số chẵn”.

Tích các số ghi trên ba thẻ đó là một số chẵn, khi trong 3 thẻ có ít nhất 1 thẻ mang số chẵn.

+) TH1: Có 1 thẻ mang số chẵn, 2 thẻ còn lại là số lẻ

Chọn 1 thẻ mang số chẵn có $C_5^1$ kết quả.

2 thẻ còn lại mang số lẻ ta có: $C_5^2$ kết quả.

Suy ra có $C_5^1.C_5^2$ cách chọn 3 thẻ trong đó có 1 thẻ là số chẵn.

+) TH2: Có 2 thẻ mang số chẵn,1 thẻ mang số lẻ

Chọn 2 thẻ mang số chẵn có $C_5^2$ kết quả.

1 thẻ mang số lẻ: $C_5^1$ kết quả.

Suy ra có $C_5^2.C_5^1$ cách chọn 3 thẻ trong đó có 2 thẻ là số chẵn và 1 thẻ mang số lẻ.

+) TH3: Có 3 thẻ mang số chẵn

Chọn 3 thẻ mang số chẵn có $C_5^3$ kết quả.

Áp dụng quy tắc cộng có $C_5^1.C_5^2+C_5^2.C_5^1+C_5^3$ = 110 kết quả.

Suy ra n(A) = 110

Vậy xác suất để xảy ra biến cố A là P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{110}{120}=\frac{11}{12}$.

Thực hành 3 trang 84 Toán lớp 10 Tập 2: Gieo đồng thời ba con xúc xắc cân đối và đồng chất. Tính xác suất của các biến cố:

a) “Tích các số chấm ở mặt xuất hiện trên ba con xúc xắc chia hết cho 3”.

b) “Tổng các số chấm ở mặt xuất hiện trên ba con xúc xắc lớn hơn 4”.

Lời giải:

Không gian mẫu là: n($\Omega$) = 6.6.6 = 216.

a) Gọi A là biến cố: “Tích các số chấm ở mặt xuất hiện trên ba con xúc xắc chia hết cho 3”.

Khi đó $\overline{A}$ là biến cố: “Tích các số chấm ở mặt xuất hiện trên ba con xúc xắc không chia hết cho 3”.

Nghĩa là số chấm xuất hiện trên ba con xúc xắc không có số nào chia hết cho 3. Do đó số chấm của 3 con xúc xắc chỉ có thể chọn trong tập {1; 2; 4; 5}. Khi đó ta có:

4.4.4 = 4³ = 64 kết quả.

⇒ n($\overline{A}$) = 64.

⇒ P($\overline{A}$) = $\frac{n\left(\overline{A}\right)}{n\left(\Omega \right)}=\frac{64}{216}=\frac{8}{27}$

⇒ P(A) = 1 – P($\overline{A}$) = $1-\frac{8}{27}=\frac{19}{27}$.

Vậy xác suất để “Tích các số chấm ở mặt xuất hiện trên ba con xúc xắc chia hết cho 3” là $\frac{19}{27}$.

b) Gọi B là biến cố “Tổng các số chấm ở mặt xuất hiện trên ba con xúc xắc lớn hơn 4”.

Khi đó $\overline{B}$ là biến cố: “Tổng các số chấm ở mặt xuất hiện trên ba con xúc xắc nhỏ hơn hoặc bằng 4”.

Các kết quả thuận lợi cho biến cố $\overline{B}$ là: {(1; 1; 1); (1; 1; 2); (1; 2; 1); (2; 1; 1)}.

⇒ n($\overline{B}$) = 4.

⇒ P($\overline{B}$) = $\frac{n\left(\overline{B}\right)}{n\left(\Omega \right)}=\frac{4}{216}=\frac{1}{54}$.

⇒ P(B) = 1 – P($\overline{B}$) = $1-\frac{1}{54}=\frac{53}{54}$.

Vậy xác suất để “Tổng các số chấm ở mặt xuất hiện trên ba con xúc xắc lớn hơn 4” là $\frac{53}{54}$.

Thực hành 4 trang 84 Toán lớp 10 Tập 2: Trong hộp có 3 bi xanh, 4 bi đỏ và 5 bi vàng có kích thước và khối lượng như nhau. Lấy ngẫu nhiên từ trong hộp 4 viên bi. Tính xác suất để trong 4 bi lấy ra:

a) Có ít nhất 1 bi xanh.

b) Có ít nhất 2 bi đỏ.

Lời giải:

Lấy ngẫu nhiên 4 viên bi từ hộp nên các kết quả của không gian mẫu là: n($\Omega$) = $C_{12}^4$ = 495.

a) Gọi A là biến cố “Có ít nhất 1 bi xanh”

Khi đó $\overline{A}$ là biến cố “Không có bi xanh” nghĩa là trong 4 bi được lấy ra chỉ có bi đỏ và bi vàng. Do đó các kết quả của biến cố $\overline{A}$ là: n($\overline{A}$) = $C_9^4$ = 126.

Xác suất để xảy ra $\overline{A}$ là: P($\overline{A}$) = $\frac{n\left(\overline{A}\right)}{n\left(\Omega \right)}=\frac{126}{495}=\frac{14}{55}$.

Xác suất để xảy ra A là: P(A) =1 – P($\overline{A}$) $=1-\frac{14}{55}=\frac{41}{55}$.

Vậy xác suất để trong 4 bi lấy ra có ít nhất 1 bi xanh là $\frac{41}{55}$.

b) Gọi B là biến cố “Trong 4 bi có ít nhất 2 bi đỏ”

Khi đó $\overline{B}$ là biến cố “Trong 4 bi có 1 bi đỏ hoặc không có bi đỏ nào”:

TH1: Có 1 bi đỏ, có $C_4^1.C_8^3$ = 224;

TH2: Không có bi đỏ, có $C_8^4$ = 70;

Do đó các kết quả của biến cố $\overline{B}$ là: n($\overline{B}$) = 224 + 70 = 294.

Xác suất để xảy ra $\overline{B}$ là: P($\overline{B}$) = $\frac{n\left(\overline{B}\right)}{n\left(\Omega \right)}=\frac{294}{495}=\frac{98}{165}$.

Xác suất để xảy ra B là: P(B) =1 – P($\overline{B}$) $=1-\frac{98}{165}=\frac{67}{165}$.

Vậy xác suất để trong 4 bi lấy ra có ít nhất 2 bi đỏ là $\frac{67}{165}$.

4. Nguyên lí xác suất bé

Khám phá 3 trang 84 Toán lớp 10 Tập 2: Có 1 hạt gạo nếp nằm lẫn trong một cái thùng chứa 10kg gạo tẻ. Lấy ngẫu nhiên 1 hạt gạo từ thùng. Theo bạn, hạt gạo lấy ra là gạo tẻ hay gạo nếp?

Lời giải:

Vì trong 10kg gạo tẻ có thể có chứa rất nhiều hạt gạo tẻ (khoảng hơn 70 nghìn hạt) mà chỉ có 1 hạt gạo nếp trong đó. Do đó việc lấy ngẫu nhiên một hạt gạo từ thùng thì hạt gạo lấy ra đa số là hạt gạo tẻ.

Bài tập (trang 85)

Giải toán lớp 10 trang 85 Tập 2 Chân trời sáng tạo

Bài 1 trang 85 Toán lớp 10 Tập 2: Tung ba con đồng xu cân đối và đồng chất. Xác định biến cố đối của mỗi biến cố sau và tính xác suất của nó.

a) “Xuất hiện ba mặt sấp”;

b) “Xuất hiện ít nhất một mặt sấp”.

Lời giải:

a) Gọi biến cố A là biến cố “Xuất hiện ba mặt sấp”.

Khi đó biến cố đối của biến cố A là biến cố $\overline{A}$: “Xuất hiện ít nhất một mặt ngửa”.

Tung ba con đồng xu cân đối và đồng chất mỗi đồng xu có hai khả năng là sấp và ngửa nên không gian mẫu là: $\Omega$ = {(N, N, N); (N, N, S); (N, S, N); (S, N, N); (N, S, S); (S, N, S); (S, S, N); (S, S, S)}.

⇒ n($\Omega$) = 8.

Các kết quả thuận lợi cho biến cố A là (S, S, S) nên n(A) = 1.

Xác suất xảy ra biến cố A là: P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{1}{8}$.

Xác suất xảy ra biến cố $\overline{A}$ là: P($\overline{A}$) =1 – P(A) $=1-\frac{1}{8}=\frac{7}{8}$.

b) Gọi biến cố B là biến cố “Xuất hiện ít nhất một mặt sấp”.

Khi đó biến cố đối của biến cố B là biến cố $\overline{B}$: “Xuất hiện ba mặt ngửa”.

Các kết quả thuận lợi cho biến cố $\overline{B}$ là (N, N, N) nên n($\overline{B}$) = 1.

Xác suất xảy ra biến cố $\overline{B}$ là: P($\overline{B}$) = $\frac{n\left(\overline{B}\right)}{n\left(\Omega \right)}=\frac{1}{8}$.

Xác suất xảy ra biến cố B là: P(B) =1 – P($\overline{B}$) $=1-\frac{1}{8}=\frac{7}{8}$.

Bài 2 trang 85 Toán lớp 10 Tập 2: Gieo hai con xúc xắc cân đối và đồng chất. Tính xác suất của mỗi biến cố sau:

a) “Tổng số chấm xuất hiện nhỏ hơn 10”;

b) “Tích số chấm xuất hiện chia hết cho 3”

Lời giải:

Khi gieo hai con xúc xắc cân đối và đồng chất thì không gian mẫu là: n($\Omega$) = 6.6 = 36.

a) Gọi A là biến cố: “Tổng số chấm xuất hiện nhỏ hơn 10”.

Các kết quả thuận lợi cho biến cố A là: A = {(1; 1); (1; 2); (1; 3); (1; 4); (1; 5); (1; 6); (2; 1); (2; 2); (2; 3); (2; 4); (2; 5); (2; 6); (3; 1); (3; 2); (3; 3); (3; 4); (3; 5); (3; 6); (4; 1); (4; 2); (4; 3); (4; 4); (4; 5); (5; 1); (5; 2); (5; 3); (5; 4); (6; 1); (6; 2); (6; 3)}.

⇒ n(A) = 30

Xác suất xảy ra biến cố A là: P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{30}{36}=\frac{5}{6}$.

b) Gọi B là biến cố: “Tích số chấm xuất hiện chia hết cho 3”.

Các kết quả thuận lợi cho biến cố B là: B = {(1; 3); (1; 6); (2; 3); (2; 6); (3; 3); (3; 6); (4; 3); (4; 6); (5; 3); (5; 6); (6; 3); (6; 6); (3; 1); (6; 1); (3; 2); (6; 2); (3; 4); (6; 4); (3; 5); (6; 5)}.

⇒ n(B) = 12

Xác suất xảy ra biến cố B là: P(B) = $\frac{n\left(B\right)}{n\left(\Omega \right)}=\frac{20}{36}=\frac{5}{9}$.

Bài 3 trang 85 Toán lớp 10 Tập 2: Hộp thứ nhất đựng thẻ xanh, 1 thẻ đỏ và 1 thẻ vàng. Hộp thứ hai đựng 1 thẻ xanh và 1 thẻ đỏ. Các tấm thẻ có kích thước và khối lượng như nhau. Lần lượt lấy ra ngẫu nhiên từ mỗi hộp một tấm thẻ:

a) Sử dụng sơ đồ hình cây, hãy liệt kê tất cả các kết quả có thể xảy ra.

b) Tính xác suất của biến cố “Trong hai thẻ lấy ra có ít nhất 1 thẻ màu đỏ”.

Lời giải:

a) Các kết quả có thể xảy ra được biểu diễn trong sơ đồ sau:

Vậy có tất cả 6 kết quả có thể xảy ra.

b) Gọi A là biến cố “Trong hai thẻ lấy ra có ít nhất 1 thẻ màu đỏ”.

Ta có sơ đồ sau:

Có 4 kết quả thuận lợi cho biến cố A.

⇒ P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{4}{6}=\frac{2}{3}.$

Bài 4 trang 85 Toán lớp 10 Tập 2: Trong hộp có một số quả bóng màu xanh và màu đỏ có kích thước và khối lượng như nhau. An nhận thấy nếu lấy ngẫu nhiên hai quả bóng từ hộp thì xác suất để hai quả bóng này khác màu là 0,6. Hỏi xác suất để hai quả bóng lấy ra cùng màu là bao nhiêu?

Lời giải:

Gọi A là biến cố “Hai quả bóng này khác màu” và B là biến cố “Hai quả bóng này cùng màu”.

Vì trong hộp chỉ có hai loại bóng là bóng màu xanh và bóng màu đỏ nên nếu lấy ngẫu nhiên hai quả bóng bất kì thì một là hai quả bóng khác màu hoặc hai quả bóng cùng màu. Do đó B là biến cố đối của A.

Do đó P(A) + P(B) = 1

⇒ P(B) = 1 – 0,6 = 0,4.

Vậy xác suất để hai quả bóng lấy ra cùng màu là 0,4.

Bài 5 trang 85 Toán lớp 10 Tập 2: Năm bạn Nhân, Lễ, Nghĩa, Trí và Tín xếp một cách ngẫu nhiên thành một hàng ngang để chụp ảnh. Tính xác suất của biến cố:

a) “Nhân và Tín không đứng cạnh nhau”;

b) “Trí không đứng ở đầu hàng”.

Lời giải:

Việc sắp xếp 5 bạn Nhân, Lễ, Nghĩa, Trí và Tín thành một hàng ngang để chụp ảnh có 5! cách xếp. Do đó không gian mẫu n($\Omega$) = 5!.

a) Gọi A là biến cố “Nhân và Tín không đứng cạnh nhau”

Khi đó $\overline{A}$ là biến cố “Nhân và Tín đứng cạnh nhau”. Do đó có thể coi hai bạn này là một bạn.

Khi đó việc sắp xếp 5 bạn Nhân, Lễ, Nghĩa, Trí và Tín thành một hàng ngang chụp ảnh sao cho Nhân và Tín đứng cạnh nhau sẽ có 4!.2! cách xếp.

⇒ n($\overline{A}$) = 4!.2!

Xác suất xảy ra $\overline{A}$ là: P($\overline{A}$) = $\frac{n\left(\overline{A}\right)}{n\left(\Omega \right)}=\frac{4!.2!}{5!}=\frac{2}{5}$.

Vì A và $\overline{A}$ là hai biến cố đối nên xác suất xảy ra A là P(A) = $1-P\left(\overline{A}\right)=1-\frac{2}{5}=\frac{3}{5}$.

Vậy xác suất để “Nhân và Tín không đứng cạnh nhau” là $\frac{3}{5}$.

b)

Gọi B là biến cố “Trí không đứng ở đầu hàng”.

Khi đó $\overline{B}$ là biến cố “Trí đứng ở đầu hàng”.

+) Nếu Trí đứng ở đầu hàng bên trái thì 4 bạn còn lại sẽ có 4! cách xếp.

+) Nếu Trí đứng ở đầu hàng bên phải thì 4 bạn còn lại sẽ có 4! cách xếp.

Suy ra có 4!.2 cách xếp sao cho Trí đứng ở đầu hàng.

⇒ P($\overline{B}$) = $\frac{n\left(\overline{B}\right)}{n\left(\Omega \right)}=\frac{4!.2}{5!}=\frac{2}{5}$

Vì B và $\overline{B}$ là hai biến cố đối nên xác suất xảy ra B là P(B) = $1-P\left(\overline{B}\right)=1-\frac{2}{5}=\frac{3}{5}$.

Vậy xác suất để “Trí không đứng ở đầu hàng” là $\frac{3}{5}$.

Xem thêm các bài giải SGK Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Không gian mẫu và biến cố

Bài tập cuối chương 10

Bài 1: Vẽ đồ thị hàm số bậc hai bằng phần mềm Geogebra

Bài 2: Vẽ ba đường conic bằng phần mềm Geogebra

Lý thuyết Xác suất của biến cố

1. Xác suất của biến cố

– Giả sử một phép thử có không gian mẫu Ω gồm hữu hạn các kết quả có cùng khả năng xảy ra và A là một biến cố.

Xác suất của biến cố A là một số, kí hiệu là P(A), được xác định bởi công thức:

P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}$   

Trong đó n(A) và n($\Omega$) lần lượt là kí hiệu số phần tử của tập A và $\Omega$ .

Chú ý:

+ Định nghĩa trên được gọi là định nghĩa cổ điển của xác suất.

+ Với mọi biến cố A, 0 ≤ P(A) ≤ 1.

+ P($\Omega$) = 1, P(∅) = 0.

+ Xác suất của mỗi biến cố đo lường xảy ra của biến cố đó. Biến cố có khả năng xảy ra càng cao thì xác suất của nó càng gần 1.

Ví dụ: Trong hộp có 3 viên bi xanh và 5 viên bi đỏ. Lấy ngẫu nhiên trong hộp 3 viên bi. Tính xác suất của biến cố A: “Lấy ra được 3 viên bi màu đỏ”.

Hướng dẫn giải

– Tính số phần tử của không gian mẫu:

Lấy 3 viên bi ngẫu nhiên trong 8 viên bi có $C_8^3$  cách.

Do đó số phần tử của không gian mẫu là n($\Omega$) = $C_8^3$ = 56.

– Tính số kết quả thuận lợi cho biến cố A:

Lấy được 3 viên bi màu đỏ trong số 5 viên bi màu đỏ có $C_5^3$  cách.

Do đó, số kết quả thuận lợi cho biến cố A là n(A) = $C_5^3$  = 10.

Xác suất của biến cố A: “Lấy ra được 3 viên bi màu đỏ” là:

P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}$  =$\frac{10}{56}=\frac{5}{28}$

Vậy xác suất của biến cố A là P(A) = $\frac{5}{28}$ .

2. Tính xác suất bằng sơ đồ hình cây

– Trong chương VIII, chúng ta đã được làm quen với phương pháp sử dụng sơ đồ hình cây để liệt kê các kết quả của một thí nghiệm. Ta cũng có thể sử dụng sơ đồ hình cây để tính xác suất

Ví dụ: Tung một đồng xu cân đối và đồng chất 3 lần liên tiếp. Tính xác suất của biến cố A: “Trong 3 lần tung có ít nhất 1 lần xuất hiện mặt ngửa”.

Hướng dẫn giải

Kí hiệu S nếu tung được mặt sấp, N nếu tung được mặt ngửa.

Các kết quả có thể xảy ra trong 3 lần tung được thể hiện trong sơ đồ hình cây dưới đây:

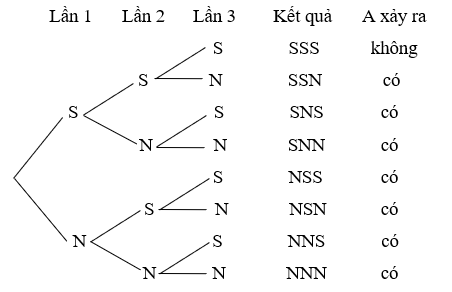
Có tất cả 8 kết quả xảy ra, trong đó có 7 kết quả thuận lợi cho biến cố A.

Do đó:

P(A) = $\frac{7}{8}$ .

3. Biến cố đối

– Cho A là một biến cố. Khi đó biến cố “Không xảy ra A”, kí hiệu là $\left(\overline{A}\right)$ , được gọi là biến cố đối của A.

$\overline{A}=\Omega \backslash A$; P$\left(\overline{A}\right)$  + P(A) = 1.

Ví dụ: Trong giỏ có 3 quả cam, 4 quả táo và 2 quả đào. Lấy ngẫu nhiên từ trong giỏ ra 4 quả. Tính xác suất để trong 4 quả lấy ra có ít nhất 1 quả táo.

Hướng dẫn giải

Gọi A là biến cố “Trong 4 quả lấy ra có ít nhất 1 quả táo”.

Thì biến cố đối của A là $\overline{A}$ : “Trong 4 quả lấy ra không có quả táo nào”.

Ta sẽ tính xác suất của biến cố $\overline{A}$ :

Lấy 4 quả trong tổng số 3 + 4 + 2 = 9 quả có  cách.

Do đó, số phần tử của không gian mẫu là n$\left(\Omega \right)$= $C_9^4$  = 126.

Lấy 4 quả trong số 5 quả cam và đào thì có $C_5^4$cách.

Do đó, số kết quả thuận lợi cho biến cố $\overline{A}$ là: n($\overline{A}$) = $C_5^4$ = 5.

Xác suất của biến cố $\overline{A}$  là: P$\left(\overline{A}\right)$ =$\frac{n\left(\overline{A}\right)}{n\left(\Omega \right)}=\frac{5}{126}$

Suy ra xác suất của biến cố A là:

P(A) = 1 – P$\left(\overline{A}\right)$ =$\frac{121}{126}$.

4. Nguyên lí xác suất bé

Trong thực tế, các biến cố có xác suất xảy ra gần bằng 1 thì gần như là luôn xảy ra trong một phép thử. Ngược lại, các biến cố mà xác suất xảy ra gần bằng 0 thi gần như không xảy ra trong một phép thử.

Trong Lí thuyết Xác suất, Nguyên lí xác suất bé được phát biểu như sau:

Nếu một biến cố có xác suất rất bé thì trong một phép thử, biến cố đó sẽ không xảy ra.

Ví dụ: Khi một con tàu lưu thông trên biển, xác suất nó bị đắm là số dương. Tuy nhiên, nếu tuân thủ các quy tắc an toàn thi xác suất xảy ra biển cố này là rất nhỏ, con tàu có thể yên tâm hoạt động.

Nếu một nhà sản xuất tuyên bố tỉ lệ gây sốc phản vệ nặng khi tiêm một loại vắc xin là rất nhỏ, chỉ khoảng 0,001, thì có thể tiêm vắc xin đó cho mọi người được không? Câu trả lời là không, vì sức khoẻ và tính mạng con người là vô giá, nếu tiêm loại vắc xin đó cho hàng tỉ người thì khả năng có nhiều người bị sốc phản vệ nặng là rất cao.