Với lời giải SBT Toán 10 trang 40 Tập 2 chi tiết trong Bài 1: Quy tắc cộng và quy tắc nhân sách Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 1: Quy tắc cộng và quy tắc nhân

Bài 6 trang 40 SBT Toán 10 Tập 2: Mã số nhân viên của một công ty có 4 kí tự, gồm một chữ cái đầu tiên (từ 6 chữ cái A, B, C, D, E, F) và tiếp theo là 3 chữ số (từ các chữ số 0; 1;...; 9). Công ty có thể tạo ra bao nhiêu mã số nhân viên theo cách này?

Lời giải:

Có 6 cách chọn chữ cái cho kí tự đầu tiên.

Với 3 kí tự tiếp theo, mỗi kí tự có 10 cách chọn từ 10 chữ số 0, 1, 2, ..., 9.

Theo quy tắc nhân, công ty có thể tạo ra 6.10.10.10 = 6000 mã số nhân viên.

Bài 7 trang 40 SBT Toán 10 Tập 2: Có các con đường nối bốn ngôi làng A, B, C, D như trong Hình 5. Có bao nhiêu cách chọn đường đi khác nhau

a) từ A qua B rồi đến D?

b) từ A đến D?

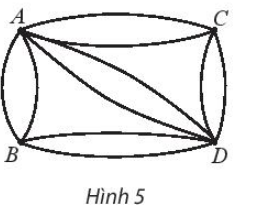
Lưu ý: Mỗi đường đi qua mỗi ngôi làng nhiều nhất một lần.

Lời giải:

a) Việc đi từ A qua B rồi đến D bao gồm hai công đoạn:

Công đoạn 1: Đi từ A đến B có 2 cách chọn.

Công đoạn 2: Ứng với mỗi cách chọn đường đi từ A đến B có 2 cách chọn đường đi từ B đến D.

Áp dụng quy tắc nhân, ta có 2.2 = 4 cách chọn con đường từ A qua B rồi đến D.

b) Đi từ A đến B có ba phương án:

Phương án 1: Đi từ A đến D qua B, có 4 cách (từ ý a).

Phương án 2: Đi thẳng từ A đến D, có 2 cách.

Phương án 3: Đi từ A đến D qua C, có 4 cách (tương tự như ý a).

Áp dụng quy tắc cộng, có 2 + 4 + 4 = 10 con đường từ A đến D.

Bài 8 trang 40 SBT Toán 10 Tập 2: Tung đồng thời hai con xúc xắc khác nhau và ghi lại số chấm xuất hiện trên mỗi con xúc xắc. Có bao nhiêu kết quả có thể xảy ra mà tổng số chấm xuất hiện trên hai mặt là bội của 5?

Lời giải:

Ta viết (a; b) để kí hiệu kết quả số chấm xuất hiện trên hai con xúc xắc lần lượt là a và b. Ta có 1 ≤ a ≤ 6 và 1 ≤ b ≤ 6 nên 2 ≤ a + b ≤ 12. Như vậy a + b là bội của 5 khi

a + b = 5 hoặc a + b = 10.

Trường hợp a + b = 5 có 4 kết quả: (1; 4), (4; 1), (2; 3), (3; 2).

Trường hợp a + b = 10 có 3 kết quả: ( 4; 6), ( 6; 4), (5; 5).

Áp dụng quy tắc cộng, ta có 4 + 3 = 7 kết quả có thể xảy ra mà tổng số chấm xuất hiện trên hai mặt là bội của 5.

Bài 9 trang 40 SBT Toán 10 Tập 2: Sử dụng 5 chữ số 0; 1; 2; 3; 4 có thể lập được bao nhiêu số tự nhiên

a) có ba chữ số khác nhau?

b) có 3 chữ số khác nhau và bé hơn 300?

c) có các chữ số khác nhau và bé hơn 100?

Lời giải:

a) Kí hiệu số có 3 chữ số khác nhau cần lập là $\overline{abc}$ trong đó a, b, c là các chữ số khác nhau từ các chữ số đã cho, a ≠ 0.

Có 4 cách chọn chữ số a là 1, 2, 3, 4.

Có 4 cách chọn chữ số b trong 5 chữ số đã cho ( b ≠ a ).

Có 3 cách chọn chữ số c trong 5 chữ số đã cho ( c ≠ b ≠ a ).

Áp dụng quy tắc nhân ta có 4.4.3 = 48 số tự nhiên thỏa mãn yêu cầu.

b) Kí hiệu số có 3 chữ số khác nhau cần lập là $\overline{abc}$ trong đó a, b, c là các chữ số khác nhau từ các chữ số đã cho, a ≠ 0.

Vì số đó < 300 nên a < 3.

Có 2 cách chọn chữ số a là 1, 2.

Có 4 cách chọn chữ số b trong 5 chữ số đã cho ( b ≠ a ).

Có 3 cách chọn chữ số c trong 5 chữ số đã cho ( c ≠ b ≠ a ).

Áp dụng quy tắc nhân ta có 2.4.3 = 24 số tự nhiên thỏa mãn yêu cầu.

c) Kí hiệu n là số tự nhiên được lập từ các chữ số đã cho, n < 100. Có hai trường hợp như sau:

Trường hợp 1: n có 1 chữ số. Có 5 số thỏa mãn được lập từ các chữ số đã cho.

Trường hợp 2: n có 2 chữ số.

Có 4 cách chọn chữ số hàng chục: 1, 2, 3, 4.

Có 4 cách chọn chữ số hàng đơn vị khác chữ số hàng chục từ các chữ số đã cho.

Áp dụng quy tắc nhân ta có 4.4 = 16 số.

Áp dụng quy tắc cộng ta có 16 + 5 = 21 số thỏa mãn yêu cầu đề bài.

Bài 10 trang 40 SBT Toán 10 Tập 2: Một khoá tổ hợp với đĩa quay có 40 vạch số (xem Hình 7). Mật mã của khoá là một dãy gồm 3 số, kí hiệu là a – b – c, mỗi số là một số tự nhiên từ 0 đến 39. Để mở khoá, cần quay mặt số ngược chiều kim đồng hồ cho đến khi điểm mốc gặp vạch số a lần thứ ba, rồi quay mặt số theo chiều ngược lại cho đến khi điểm mốc gặp vạch số b lần thứ hai, cuối cùng quay mặt số ngược chiều kim đồng hồ cho đến khi điểm mốc gặp vạch số c lần đầu tiên. Nếu a, b, c phải khác nhau đôi một, thì có bao nhiêu cách chọn mật mã cho khoá tổ hợp trên?

Lời giải:

Có 40 cách chọn a từ các số từ 0 đến 39.

Có 39 cách chọn b từ 39 số khác a còn lại.

Có 38 cách chọn c từ 38 số khác a và b còn lại.

Áp dụng quy tắc nhân ta có 40.39.38 = 59280 cách chọn mật mã cho khoá tổ hợp trên.

Xem thêm các bài giải sách bài tập Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Giải SBT Toán 10 trang 39 Tập 2

Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 7

Bài 1: Quy tắc cộng và quy tắc nhân

Bài 2: Hoán vị, chỉnh hợp và tổ hợp

Bài 3: Nhị thức Newton

Bài tập cuối chương 8