Với giải bài 46 trang 124 Toán lớp 8 chi tiết trong Bài 9: Thể tích của hình chóp đều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

Giải bài tập Toán lớp 8 Bài 9: Thể tích của hình chóp đều

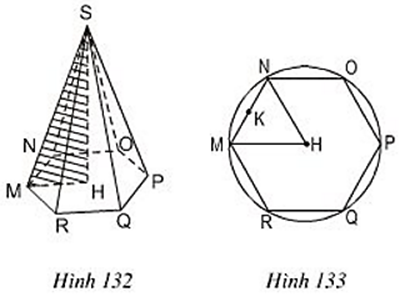
Bài 46 trang 124 Toán 8 Tập 2: S.MNOPQR là một hình chóp lục giác đều (h.132). Bán kính đường tròn ngoại tiếp đáy (đường tròn tâm H, đi qua sáu đỉnh của đáy) HM = 12cm (h.133), chiều cao SH = 35cm. Hãy tính:

a) Diện tích đáy và thể tích của hình chóp (biết $\sqrt{108}$ ≈ 10,39);

b) Độ dài cạnh bên SM và diện tích toàn phần của hình chóp (biết $\sqrt{1333}$ ≈ 36,51).

Lời giải:

a)

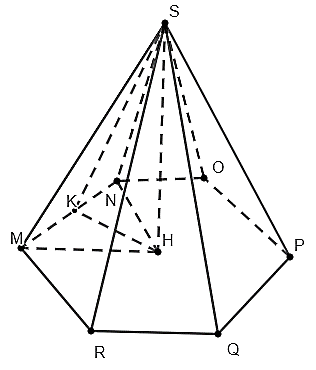
Tam giác HMN là tam giác đều. Đường cao là :

$$\begin{gathered} HK=\sqrt{H{M}^2-K{M}^2} \\ =\sqrt{{12}^2-6^2} \\ =\sqrt{108}\approx 10,39cm \end{gathered}$$(với K là trung điểm của MN)

Diện tích đáy của hình chóp lục giác đều chính là 6 lần diện tích của tam giác đều HMN. Nên:

$$\begin{gathered} S_d=6.\frac{1}{2}.MN.HK \\ =6.\frac{1}{2}\mathrm{.12.10},39=374,04c{m}^2 \end{gathered}$$

Thể tích của hình chóp:

$$\begin{gathered} V=\frac{1}{3}{S}_d.SH \\ =\frac{1}{3}.\text{\hspace{0.17em}\hspace{0.17em}}374,04.35 \\ \text{\hspace{0.17em}}=4363,8c{m}^3\text{} \end{gathered}$$

b) Trong tam giác vuông SMH vuông tại H có:

$S{M}^2=S{H}^2+H{M}^2$(định lý Py – ta – go)

$$\begin{gathered} \Rightarrow SM=\sqrt{SH{}_2+\text{\hspace{0.17em}}M{H}^2} \\ =\sqrt{{35}^2+\text{\hspace{0.17em}}{12}^2} \\ =\sqrt{1369}=37cm \end{gathered}$$

Xét tam giác SMK vuông tại K ta có:

$S{M}^2=K{M}^2+S{K}^2$ (định lý Py – ta – go)

$$\begin{gathered} \Rightarrow h=SK=\sqrt{S{M}^2-K{M}^2} \\ =\sqrt{{37}^2-6^2}=\sqrt{1333}\approx 36,51cm \end{gathered}$$

Khi đó chiều cao mỗi cạnh bên là h = 36,51cm

Diện tích xung quanh của hình chóp là:

$$\begin{gathered} S_{xq}=p.d=\frac{1}{2}.6.MN.SK \\ =\frac{1}{2}.6.12.36,51=1314,36c{m}^2 \end{gathered}$$

Diện tích toàn phần:

S_tp = S_xq + S_d = 1314, 36 + 374,04 = 1688,4cm²

Xem thêm lời giải bài tập Toán lớp 8 hay, chi tiết khác:

Câu hỏi 1 trang 123 Toán 8 Tập 2: Thực hiện các bước vẽ hình chóp đều theo chiều mũi tên đã chỉ ra trên hình 128...

Bài 44 trang 123 Toán 8 Tập 2: Hình 129 là một cái lều ở trại hè của học sinh kèm theo các kích thước...

Bài 45 trang 124 Toán 8 Tập 2: Tính thể tích của mỗi hình chóp đều dưới đây (h.130, h.131)...

Bài 48 trang 125 Toán 8 Tập 2: Tính diện tích toàn phần của:...

Bài 49 trang 125 Toán 8 Tập 2: Tính diện tích xung quanh của các hình chóp tứ giác đều sau đây (h.135):...

Bài 50 trang 125 Toán 8 Tập 2: a) Tính thể tích của hình chóp đều (h.136)...