Tailieumoi.vn xin giới thiệu Giải bài tập Toán 8 Bài 9: Thể tích của hình chóp đều hay, chi tiết giúp học sinh dễ dàng làm bài tập Thể tích của hình chóp đều lớp 8.

Giải bài tập Toán lớp 8 Bài 9: Thể tích của hình chóp đều

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 123 Toán 8 Tập 2: Thực hiện các bước vẽ hình chóp đều theo chiều mũi tên đã chỉ ra trên hình 128.

Lời giải:

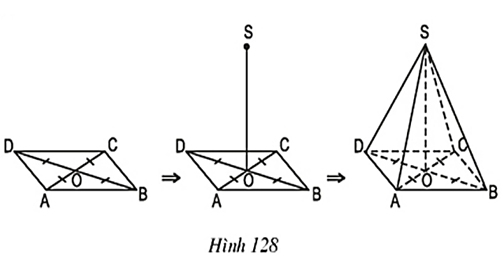
Bài tập (trang 123; 124; 125)

Bài 44 trang 123 Toán 8 Tập 2: Hình 129 là một cái lều ở trại hè của học sinh kèm theo các kích thước.

a) Thể tích không khí bên trong lều là bao nhiêu?

b) Xác định số vải bạt cần thiết để dựng lều (không tính đến đường viền, nếp gấp, ... biết  $\sqrt{5}$≈ 2,24).

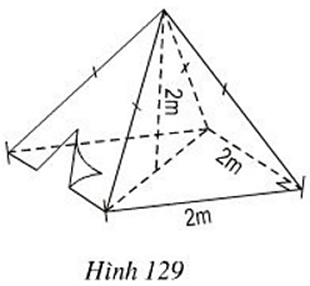
Lời giải:

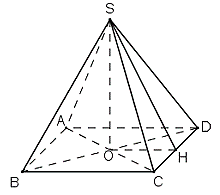
a) Lều là hình chóp đều có đáy là hình vuông cạnh bằng 2m, chiều cao bằng 2m.

Thể tích không khí trong lều bằng thể tích lều và bằng:

$V=\frac{1}{3}.\mathrm{2.2.2}=\frac{8}{3}{m}^3$

b) Số vải bạt cần thiết đề dựng lều chính là diện tích xung quanh của lều.

Dựng trung đoạn SH, H là trung điểm của CD. Vì SO vuông góc với mp (ABCD) nên SO vuông góc với OH.

Lại có O là trung điểm của BD, H là trung điểm của CD nên OH là đường trung bình của tam giác BCD

$\Rightarrow OH=\frac{1}{2}BC=\frac{1}{2}.2=1m$

Xét tam giác SOH vuông tại O ta có:

$S{H}^2=S{O}^2+O{H}^2$ (định lý Py – ta – go)

$$\begin{gathered} \iff S{H}^2=1^2+2^2=5 \\ \Rightarrow SH=\sqrt{5}cm \end{gathered}$$

Diện tích vải bạt cần dùng để dựng lều là

$S_{xq}=p.d=\frac{1}{2}\mathrm{.2.4.}\sqrt{5}=4\sqrt{5}{m}^2$

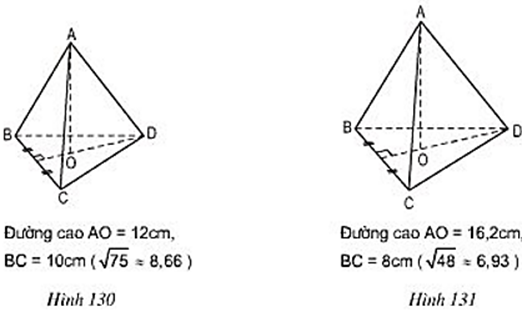
Bài 45 trang 124 Toán 8 Tập 2: Tính thể tích của mỗi hình chóp đều dưới đây (h.130, h.131).

Lời giải:

+ Hình 130.

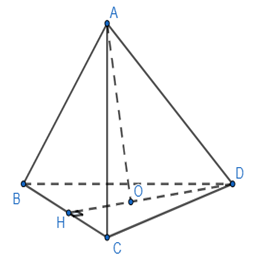
Đáy của hình chóp là tam giác đều cạnh bằng 10 cm.

Đường cao của tam giác đều DBC là:

$$\begin{gathered} h=\sqrt{D{C}^2-H{C}^2} \\ =\sqrt{{10}^2-5^2} \\ =\sqrt{75}\approx 8,66cm \end{gathered}$$ 

(với H là trung điểm cạnh BC)

Diện tích đáy của hình chóp đều là:

$S=\frac{1}{2}BC.h=\frac{1}{2}\mathrm{.10.}8,66=43,3c{m}^2$

Thể tích hình chóp là:

$V=\frac{1}{3}S.h_1=\frac{1}{3}.43,3.12=173,2c{m}^3$

+ Hình 131

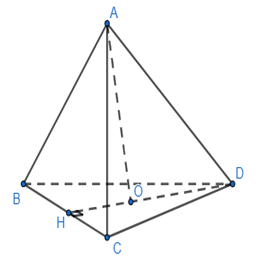
Đường cao của tam giác đều BCD là:

$$\begin{gathered} h=\sqrt{D{C}^2-H{C}^2} \\ =\sqrt{8^2-4^2}=\sqrt{48} \\ \approx 6,93cm \end{gathered}$$

Diện tích đáy của hình chóp đều:

$$\begin{gathered} S=\frac{1}{2}.BC.h \\ =\frac{1}{2}.8.6,93 \\ =27,72c{m}^2 \end{gathered}$$

Thể tích của hình chóp là:

$$\begin{gathered} V=\frac{1}{3}.S.h_1 \\ =\frac{1}{3}.27,72.16,2 \\ =149,69c{m}^3 \end{gathered}$$

Bài 46 trang 124 Toán 8 Tập 2: S.MNOPQR là một hình chóp lục giác đều (h.132). Bán kính đường tròn ngoại tiếp đáy (đường tròn tâm H, đi qua sáu đỉnh của đáy) HM = 12cm (h.133), chiều cao SH = 35cm. Hãy tính:

a) Diện tích đáy và thể tích của hình chóp (biết $\sqrt{108}$ ≈ 10,39);

b) Độ dài cạnh bên SM và diện tích toàn phần của hình chóp (biết $\sqrt{1333}$ ≈ 36,51).

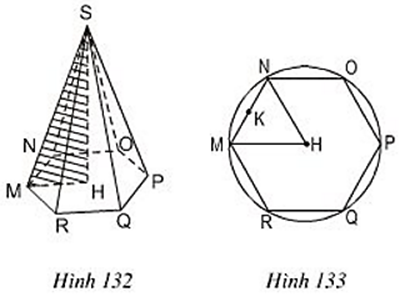
Lời giải:

a)

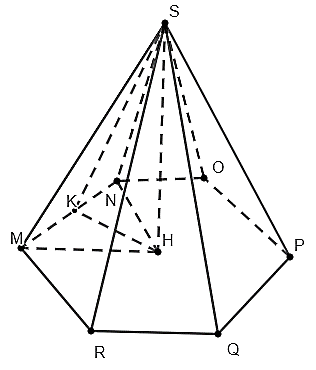
Tam giác HMN là tam giác đều. Đường cao là :

$$\begin{gathered} HK=\sqrt{H{M}^2-K{M}^2} \\ =\sqrt{{12}^2-6^2} \\ =\sqrt{108}\approx 10,39cm \end{gathered}$$(với K là trung điểm của MN)

Diện tích đáy của hình chóp lục giác đều chính là 6 lần diện tích của tam giác đều HMN. Nên:

$$\begin{gathered} S_d=6.\frac{1}{2}.MN.HK \\ =6.\frac{1}{2}\mathrm{.12.10},39=374,04c{m}^2 \end{gathered}$$

Thể tích của hình chóp:

$$\begin{gathered} V=\frac{1}{3}{S}_d.SH \\ =\frac{1}{3}.\text{\hspace{0.17em}\hspace{0.17em}}374,04.35 \\ \text{\hspace{0.17em}}=4363,8c{m}^3\text{} \end{gathered}$$

b) Trong tam giác vuông SMH vuông tại H có:

$S{M}^2=S{H}^2+H{M}^2$(định lý Py – ta – go)

$$\begin{gathered} \Rightarrow SM=\sqrt{SH{}_2+\text{\hspace{0.17em}}M{H}^2} \\ =\sqrt{{35}^2+\text{\hspace{0.17em}}{12}^2} \\ =\sqrt{1369}=37cm \end{gathered}$$

Xét tam giác SMK vuông tại K ta có:

$S{M}^2=K{M}^2+S{K}^2$ (định lý Py – ta – go)

$$\begin{gathered} \Rightarrow h=SK=\sqrt{S{M}^2-K{M}^2} \\ =\sqrt{{37}^2-6^2}=\sqrt{1333}\approx 36,51cm \end{gathered}$$

Khi đó chiều cao mỗi cạnh bên là h = 36,51cm

Diện tích xung quanh của hình chóp là:

$$\begin{gathered} S_{xq}=p.d=\frac{1}{2}.6.MN.SK \\ =\frac{1}{2}.6.12.36,51=1314,36c{m}^2 \end{gathered}$$

Diện tích toàn phần:

S_tp = S_xq + S_d = 1314, 36 + 374,04 = 1688,4cm²

Bài 48 trang 125 Toán 8 Tập 2: Tính diện tích toàn phần của:

a) Hình chóp tứ giác đều, biết cạnh đáy a = 5cm, cạnh bên b = 5cm,

$\sqrt{18,75}$ ≈ 4,33;

b) Hình chóp lục giác đều, biết cạnh đáy a = 6cm, cạnh bên b = 10cm, $\sqrt{3}$ ≈ 1,73; $\sqrt{91}$ ≈ 9,54.

Lời giải:

a)

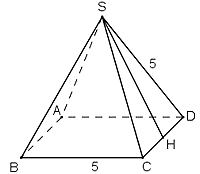
Hình chóp SABCD có SA = 5 và BC = 5 nên các mặt bên của hình chóp này đều là những tam giác đều. Vẽ SH vuông góc với CD tại H nên H là trung điểm của CD.

Do tam giác SHC vuông tại H nên:

$$\begin{gathered} SH=\sqrt{S{C}^2-H{C}^2} \\ =\sqrt{5^2-2,5^2} \\ =\sqrt{18,75}\approx 4,33cm \end{gathered}$$ (với H là trung điểm cạnh CD)

Diện tích xung quanh của hình chóp:

$S_{xq}=p.d=\frac{1}{2}.\mathrm{5.4.}4,33=43,3c{m}^2$

Diện tích đáy là: S_d = 5²  = 25 cm²

Diện tích toàn phần:

S_tp = S_xq + S_d = 43,3 + 25 = 68,3cm²

b)

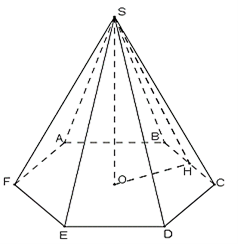
Gọi H là trung điểm của BC. Tam giác SBC cân có SH là đường trung tuyến nên đồng thời là đường cao.

Mặt bên của hình chóp lục giác đều là tam giác cân có cạnh bên 10cm, cạnh đáy 6cm.

Đường cao SH của mặt bên là:

$$\begin{gathered} SH=\sqrt{S{B}^2-B{H}^2} \\ =\sqrt{{10}^2-3^2} \\ =\sqrt{91}\approx 9,54cm \end{gathered}$$

Diện tích xung quanh của hình chóp:

$S_{xq}=p.d=\frac{1}{2}.\mathrm{6.6.}9,54=171,72c{m}^2$

Đáy của hình chóp là lục giác đều. Diện tích của lục giác bằng 6 lần diện tích tam  giác đều ABO.

Chiều cao của tam giác đều ABO là:

$$\begin{gathered} OH=\sqrt{O{B}^2-B{H}^2} \\ =\sqrt{6^2-3^2}=\sqrt{27}\approx 5,2cm \end{gathered}$$

Diện tích đáy của hình chóp là:

$S_d=6.\frac{1}{2}.6.5,2=93,6c{m}^2$

Diện tích toàn phần của hình chóp là:

S_tp = S_xq + S_đ = 171,72 + 93,6 = 265,32(cm²)

Bài 49 trang 125 Toán 8 Tập 2: Tính diện tích xung quanh của các hình chóp tứ giác đều sau đây (h.135):

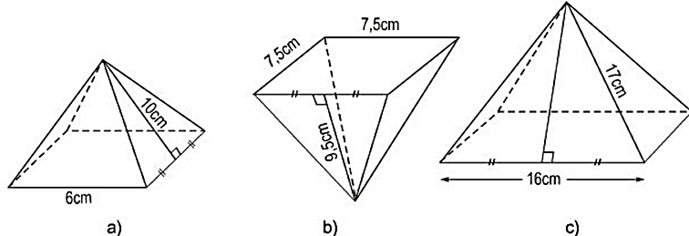
Lời giải:

Hình a: Diện tích xung quanh là:

$S_{xq}=p.d=\frac{1}{2}.\mathrm{6.4.10}=120c{m}^2$

Hình b: 

$S_{xq}=p.d=\frac{1}{2}.7,5.4.9,5=142,5c{m}^2$

Hình c:

Độ dài trung đoạn:

$d=\sqrt{{17}^2-8^2}=\sqrt{225}=15$(định lý Py – ta – go)

$$\begin{gathered} \Rightarrow S_{xq}=p.d \\ =\frac{1}{2}.16.4.15 \\ =480c{m}^2 \end{gathered}$$

Bài 50 trang 125 Toán 8 Tập 2: a) Tính thể tích của hình chóp đều (h.136).

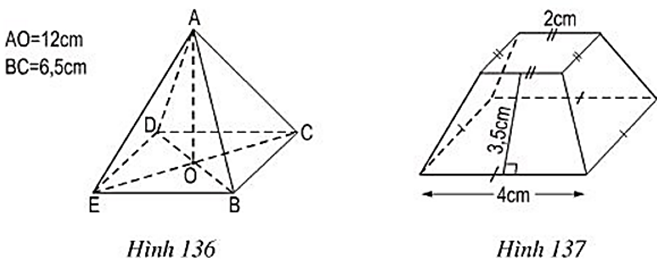
b) Tính diện tích xung quanh của hình chóp cụt đều (h.137).

(Hướng dẫn: Diện tích cần tính bằng tổng diện tích các mặt xung quanh. Các mặt xung quanh là những hình thang cân với cùng chiều cao, các cạnh đáy tương ứng bằng nhau, các cạnh bên bằng nhau).

Lời giải:

a) Diện tích đáy của hình chóp là:

S = BC² = 6,5² =  42,25 cm²

Thể tích của hình chóp là:

$V=\frac{1}{3}.S.h=\frac{1}{3}.42,25.12=169c{m}^3$

b) Các mặt xung quanh của hình chóp cụt là những hình thang cân có đáy nhỏ là 2 cm; đáy lớn 4 cm và chiều cao 3,5 cm.

Diện tích xung quanh là:

$S{}_{xq}=4.\frac{(2+\text{\hspace{0.17em}}4).3,5}{2}=42c{m}^2$