Với lời giải SBT Toán 10 trang 26 Tập 2 chi tiết trong Bài tập cuối chương 6 sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài tập cuối chương 6

Bài 6.55 trang 26 SBT Toán 10 Tập 2: Cho hàm số $y=\left\{\begin{array}{c}2x+3khi-2\le x<-1\\ \frac{1}{2}x+\frac{3}{2}khi-1\le x<1\\ -\frac{1}{2}x+\frac{9}{2}khi1\le x\le 3\end{array}\right.$.

a) Tìm tập xác định của hàm số.

b) Vẽ đồ thị hàm số.

c) Từ đồ thị vẽ ở ý b) hãy chỉ ra các khoảng đồng biến, khoảng nghịch biến của hàm số.

d) Tìm tập giá trị của hàm số.

Lời giải:

a)

Tập xác định của hàm số là tập giá trị của x là đoạn D = [–2; 3].

b)

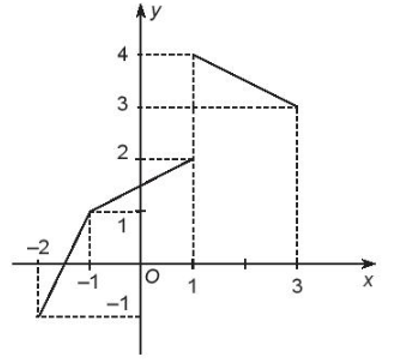
Trên nửa khoảng [–2; –1), đồ thị hàm số là đoạn thẳng đi qua điểm (–2; –1) và (–1,5; 0)

Trên nửa khoảng [–1; 1), đồ thị hàm số là đoạn thẳng đi qua điểm (–1; 1) và (0; 1,5)

Trên đoạn [1; 3], đồ thị hàm số là đoạn thẳng đi qua điểm (1; 4) và (3; 3).

Vậy ta vẽ được đồ thị hàm số như hình dưới đây

c)

Đồ thị hàm số đi lên từ trái sang phải trên khoảng (–2; 1) và đi xuống trên khoảng (1; 3)

Vậy hàm số đồng biến trên khoảng (–2; 1) và nghịch biến trên khoảng (1; 3).

d)

Dựa vào đồ thị ta thấy tập giá trị của hàm số là [–1; 2) ∪ [3; 4].

Bài 6.56 trang 26 SBT Toán 10 Tập 2: Với mỗi hàm số dưới đây, hãy vẽ đồ thị, tìm tập xác định, tập giá trị, khoảng đồng biến và khoảng nghịch biến của chúng.

a) y = |x – 1| + |x + 1|;

b) $y=\left\{\begin{array}{c}x+1khix<-1\\ x^2-1khix\ge -1\end{array}\right.$.

Lời giải:

a)

y = |x – 1| + |x + 1|

Hàm số có tập xác định là: D = ℝ

$y=\left|x-1\right|+\left|x+1\right|=\left\{\begin{array}{c}-2xkhix<-1\\ 2khi-1\le x<1\\ 2xkhix\ge 1\end{array}\right.$.

Trên khoảng (–∞; –1), đồ thị hàm số là đường thẳng y = –2x

Trên nửa khoảng [–1; 1), đồ thị hàm số là đường thẳng y = 2 (song song với trục Ox)

Trên nửa khoảng [1; +∞), đồ thị hàm số là đường thẳng y = 2x

Khi x = –1 thì y = 2 nên đồ thị hàm số đi qua điểm (–1; 2)

Khi x = 1 thì y = 2 nên đồ thị hàm số đi qua điểm (1; 2)

Ta vẽ được đồ thị hàm số như sau:

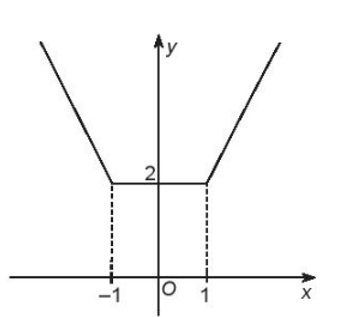
Dựa vào đồ thị có:

- Tập giá trị của hàm số là T = [2; +∞).

- Đồ thị hàm số đi xuống từ trái sang phải trên khoảng (–∞; –1), đi lên trên từ trái sang phải trên khoảng (1; +∞), và song song với trục Ox trên khoảng (–1; 1).

Do đó, hàm số này nghịch biến trên khoảng (–∞; –1), đồng biến trên khoảng (1; +∞), và là hàm hằng trên (–1; 1).

b)

Tập xác định hàm số là D = ℝ.

$y=\left\{\begin{array}{c}x+1khix<-1\\ x^2-1khix\ge -1\end{array}\right.$

Đồ thị hàm số là đường thẳng y = x + 1 trên khoảng (–∞; –1), đường thẳng này đi qua điểm (–2; –1) và (–3; –2).

Đồ thị hàm số là parabol y = x² – 1 trên nửa khoảng [–1; +∞), parabol này có đỉnh (0; –1), trục đối xứng x = 0 (trục Oy) và đi qua điểm (–1; 0) và (1; 0).

Ta vẽ được đồ thị hàm số như sau:

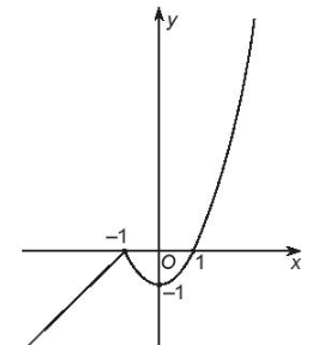
Dựa vào đồ thị ta có:

- Tập giá trị của hàm số là: T = ℝ.

- Đồ thị hàm số đi lên từ trái sang phải trên các khoảng (–∞; –1) và (0; +∞), đi xuống từ trái sang phải trên khoảng (–1; 0).

Do đó, hàm số này đồng biến trên khoảng (–∞; –1) và (0; +∞), nghịch biến trên khoảng (–1; 0).

Bài 6.57 trang 26 SBT Toán 10 Tập 2: Dựa vào đồ thị của hàm số y = ax² + bx + c, hãy xác định dấu của các hệ số a, b, c trong mỗi trường hợp dưới đây.

Lời giải:

a)

Xét hình (a) ta có:

Parabol có bề lõm hướng xuống nên a < 0

Parabol cắt trục Oy tại điểm có tung độ dương nên c > 0

Parabol có đỉnh có hoành độ là: $-\frac{b}{2a}$ < 0. Mà a < 0 nên b < 0

Vậy a < 0, c > 0, b < 0.

b)

Xét hình (b) ta có:

Parabol có bề lõm hướng lên nên a > 0

Parabol cắt trục Oy tại điểm có tung độ dương nên c > 0

Parabol có đỉnh có hoành độ là: $-\frac{b}{2a}$ > 0. Mà a > 0 nên b < 0

Vậy a > 0, c > 0, b < 0.

c)

Xét hình (c) ta có:

Parabol có bề lõm hướng lên nên a > 0

Parabol cắt trục Oy tại gốc tọa độ nên c = 0.

Parabol có đỉnh có hoành độ là: $-\frac{b}{2a}$ < 0. Mà a > 0 nên b > 0

Vậy a > 0, c = 0, b > 0.

d)

Xét hình (d) ta có:

Parabol có bề lõm hướng xuống nên a < 0

Parabol cắt trục Oy tại điểm có tung độ âm nên c < 0

Parabol có đỉnh có hoành độ là: $-\frac{b}{2a}$ > 0. Mà a < 0 nên b > 0

Vậy a < 0, c < 0, b > 0.

Bài 6.58 trang 26 SBT Toán 10 Tập 2: Trong mỗi trường hợp dưới đây, hãy vẽ đồ thị của các hàm số trên cùng một mặt phẳng toạ độ rồi xác định toạ độ giao điểm của chúng:

a) y = –x + 3 và y = –x² – 4x + 1.

b) y = 2x – 5 và y = x² – 4x – 1.

Lời giải:

a)

Đồ thị hàm số y = –x + 3 là đường thẳng đi qua điểm (0; 3), (–1; 4) và (3; 0)

Đồ thị hàm số y = –x² – 4x + 1 là parabol có bề lõm hướng xuống, đỉnh là điểm (–2; 5), trục đối xứng x = –2, đi qua các điểm (0; 1) và (–1; 4)

Đồ thị hai hàm số như hình vẽ:

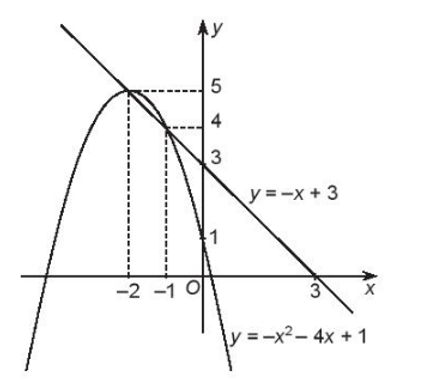
Toạ độ giao điểm của chúng là: (–1; 4) và (–2; 5).

b)

Đồ thị hàm số y = 2x – 5 là đường thẳng đi qua điểm (0; –5), (2,5; 0)

Đồ thị hàm số y = x² – 4x – 1 là parabol có bề lõm hướng lên, đỉnh là điểm (2; –5), trục đối xứng x = 2, đi qua điểm (0; –1).

Đồ thị hai hàm số như hình vẽ:

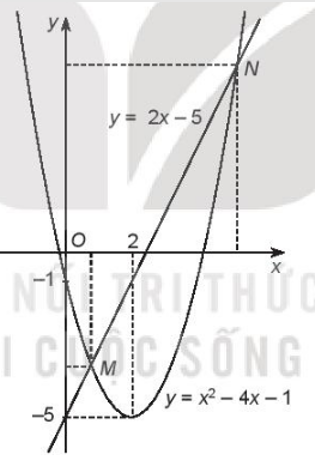
Hai đồ thị hàm số có giao điểm là M và N

Xét phương trình hoành độ giao điểm của hai đồ thị:

x²  – 4x – 1 = 2x – 5

⇔ x² – 6x  + 4 = 0

⇔ $x=3-\sqrt{5}$ hoặc $x=3+\sqrt{5}$

Với $x=3-\sqrt{5}$ ta được $y=2.\left(3-\sqrt{5}\right)-5=1-2\sqrt{5}$. Vậy $M\left(3-\sqrt{5};1-2\sqrt{5}\right)$.

Với $x=3+\sqrt{5}$ ta được $y=2.\left(3+\sqrt{5}\right)-5=1+2\sqrt{5}$. Vậy $N\left(3+\sqrt{5};1+2\sqrt{5}\right)$.

Bài 6.59 trang 26 SBT Toán 10 Tập 2: Vẽ đồ thị mỗi hàm số sau, từ đó suy ra tập nghiệm của bất phương trình tương ứng

a) y = x² – 3x + 2 và bất phương trình: x² – 3x + 2 ≥ 0;

b) y = x² – x – 6 và bất phương trình: x² – x – 6 < 0.

Lời giải:

a)

Đồ thị hàm số y = x² – 3x + 2 là parabol có bề lõm hướng lên, đỉnh là (1,5; –0,25), đi qua hai điểm (1; 0) và (2; 0). Đồ thị hàm số như hình vẽ:

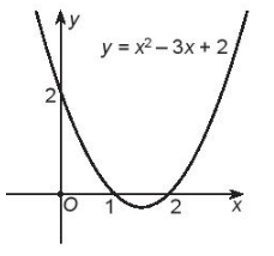
Việc giải bất phương trình x² – 3x + 2 ≥ 0 ứng với việc tìm các khoảng mà phần đồ thị tương ứng của nó nằm phía trên trục hoành. Từ đồ thị trên ta thấy khi x ≤ 1 và x ≥ 2 thì đồ thị hàm số y = x² – 3x + 2 nằm phía trên trục hoành.

Vậy tập nghiệm của bất phương trình là (–∞; 1]∪[2; +∞).

b)

Đồ thị hàm số y = x² – x – 6 là parabol có bề lõm hướng lên, đỉnh là: (0,5; –6,25), đi qua hai điểm (–2; 0), (3; 0) được vẽ trong hình sau:

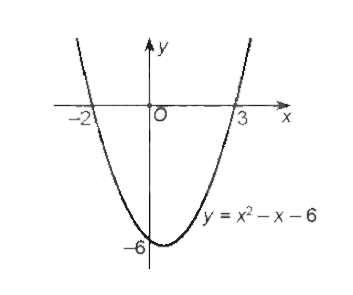
Việc giải bất phương trình y = x² – x – 6 < 0 ứng với việc tìm các khoảng mà phần đồ thị tương ứng của nó nằm phía dưới trục hoành. Từ đồ thị trên ta thấy khi –2 < x < 3 thì đồ thị hàm số y = x² – x – 6 nằm phía dưới trục hoành.

Vậy tập nghiệm của bất phương trình là (–2; 3).

Bài 6.60 trang 26 SBT Toán 10 Tập 2: Tìm các giá trị của tham số m để:

a) Hàm số $y=\frac{1}{\sqrt{m{x}^2-2mx+5}}$ có tập xác định ℝ;

b) Tam thức bậc hai y = –x² + mx – 1 có dấu không phụ thuộc vào x;

c) Hàm số $y=\sqrt{-2x^2+mx-m-6}$ có tập xác định chỉ gồm một phần tử.

Lời giải:

a)

Hàm số $y=\frac{1}{\sqrt{m{x}^2-2mx+5}}$ có tập xác định là ℝ nếu và chỉ nếu mx² – 2mx + 5 > 0 với mọi số thực x

- Khi m = 0 thì hàm số cho bởi công thức $y=\frac{1}{\sqrt{5}}$lúc này hàm số có tập xác định là ℝ.

- Khi m ≠ 0 thì mx² – 2mx + 5 > 0 với mọi số thực x nếu và chỉ nếu a = m > 0 và ∆’ = m² – 5m < 0

Xét tam thức bậc hai: f(m) = m² – 5m có:

a = 1 > 0, ∆_m = (–5)² – 4.1.0 = 25 > 0

f(m) = 0 có hai nghiệm phân biệt là: m = 0 hoặc m = 5

Do đó, m² – 5m < 0 ⇔ 0 < m < 5

Vậy hàm số đã cho xác định trên ℝ nếu và chỉ nếu 0 ≤ m < 5.

b)

Tam thức y = –x² + mx – 1 có dấu không phụ thuộc vào x khi và chỉ khi

∆ = m²  – 4 < 0 

⇔ m² < 4

⇔ –2 < m < 2.

Vậy tam thức y = –x² + mx – 1 có dấu không phụ thuộc vào x khi 2 < m < 2.

c)

Ta có:

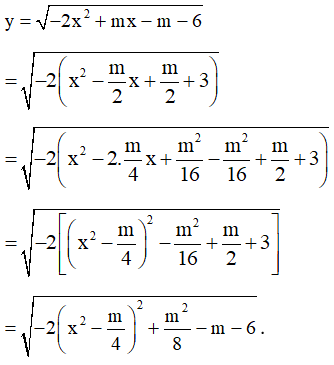
Hàm số $y=\sqrt{-2x^2+mx-m-6}$ có tập xác định chỉ gồm một phần tử khi và chỉ khi nó có dạng $y=\sqrt{-2{\left(x+\alpha \right)}^2}$. Điều này tương đương với

$\frac{m^2}{8}-m-6=0$

⇔ m­² – 8m – 48  = 0

⇔ m = –4 hoặc m = 12

Vậy khi m = –4 hoặc m = 12 thì hàm số $y=\sqrt{-2x^2+mx-m-6}$có tập xác định chỉ gồm một phần tử.

Xem thêm các bài giải sách bài tập Toán 10 Kết nối tri thức hay, chi tiết khác:

Giải SBT Toán 10 trang 22 Tập 2

Giải SBT Toán 10 trang 23 Tập 2

Giải SBT Toán 10 trang 24 Tập 2

Giải SBT Toán 10 trang 25 Tập 2

Giải SBT Toán 10 trang 27 Tập 2

Xem thêm các bài giải SBT Toán 10 Kết nối tri thức hay, chi tiết khác:

Bài 18: Phương trình quy về phương trình bậc hai

Bài tập cuối chương 6

Bài 19: Phương trình đường thẳng

Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách

Bài 21: Đường tròn trong mặt phẳng tọa độ