Với giải  34 trang 127 Toán lớp 8 chi tiết trong Bài 5: Diện tích hình thoi giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

Giải bài tập Toán lớp 8 Bài 5: Diện tích hình thoi

Bài 34 trang 127 Toán 8 Tập 1:Cho một hình chữ nhật. Vẽ tứ giác có các đỉnh là trung điểm các cạnh của hình chữ nhật. Vì sao tứ giác này là một hình thoi? So sánh diện tích hình chữ nhật, từ đó suy ra cách tính diện tích hình thoi.

Lời giải:

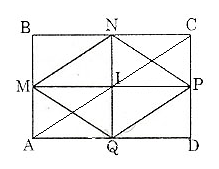
Vẽ hình chữ nhật ABCD với các trung điểm các cạnh AB, BC, CD, AD lần lượt là M, N, P, Q.

Vẽ tứ giác MNPQ

Xét tam giác ABC, có:

M là trung điểm của AB

N là trung điểm của BC

Suy ra MN là đường trung bình của tam giác ABC

$\Rightarrow MN=\frac{1}{2}AC$ và MN // AC (1)

Xét tam giác ADC, có:

P là trung điểm của DC

Q là trung điểm của AD

Suy ra PQ là đường trung bình của tam giác ADC

$\Rightarrow PQ=\frac{1}{2}AC$ và PQ // AC (2)

Từ (1) và (2) suy ra MN = PQ và MN // PQ

Tứ giác MNPQ có MN = PQ và MN // PQ nên MNPQ là hình bình hành.

Xét tam giác BDC, có:

N là trung điểm của BC

P là trung điểm của CD

Suy ra NP là đường trung bình của tam giác BDC

$\Rightarrow PN=\frac{1}{2}BD$ (3)

Mà ABCD là hình chữ nhật nên AC = BD (4)

Từ (1), (2) và (3) suy ra: MN = PN

Suy ra hình bình hành MNPQ có hai cạnh kề MN = PN nên MNPQ là hình thoi.

+ Ta có:

Diện tích hình thoi MNPQ là: $S_{MNPQ}=\frac{1}{2}MQ.NP$

Diện tích hình chữ nhật ABCD là: $S_{ABCD}=AB.BC$

Ta có ABCD là hình chữ nhật nên ABCD là hình thang, có:

M là trung điểm của AB

Q là trung điểm của CD

Suy ra MQ là đường trung bình của hình thang ABCD

$\Rightarrow MQ=\frac{1}{2}\left(AB+CD\right)=\frac{1}{2}\left(AB+AB\right)=AB$

Chứng minh tương tự NP = BC.

Do đó $S_{MNPQ}=\frac{1}{2}{S}_{ABCD}.$

Vậy diện tích hình thoi bằng nửa tích hai đường chéo.

Xem thêm lời giải bài tập Toán lớp 8 hay, chi tiết khác:

Câu hỏi 1 trang 127 Toán 8 Tập 1: Hãy tính diện tích tứ giác ABCD theo AC, BD, biết AC ⊥ BD tại H (h.145)...

Câu hỏi 2 trang 127 Toán 8 Tập 1:Hãy viết công thức tính diện tích hình thoi theo hai đường chéo...

Câu hỏi 3 trang 127 Toán 8 Tập 1: Hãy tính diện tích hình thoi bằng cách khác...

Bài 32 trang 127 Toán 8 Tập 1: a) Hãy vẽ một tứ giác có độ dài hai đường chéo là: 3,6 cm, 6cm và hai đường chéo đó vuông góc với nhau. Có thể vẽ được bao nhiêu tứ giác như vậy? Hãy tính diện tích mỗi tứ giác vừa vẽ...

Bài 33 trang 127 Toán 8 Tập 1:Vẽ hình chữ nhật có một cạnh bằng đường chéo của một hình thoi cho trước và có diện tích bằng diện tích của hình thoi đó. Từ đó suy ra cách tính diện tích hình thoi...

Bài 35 trang 128 Toán 8 Tập 1:Tính diện tích hình thoi có cạnh dài 6cm và một trong các góc của nó có số đo là 60^o...

Bài 36 trang 128 Toán 8 Tập 1:Cho một hình thoi và một hình vuông có cùng chu vi. Hỏi hình nào có diện tích lớn hơn? Vì sao?...