Tailieumoi.vn xin giới thiệu Giải bài tập Toán 8 Bài 5: Diện tích hình thoi hay, chi tiết giúp học sinh dễ dàng làm bài tập Diện tích hình thoi lớp 8.

Giải bài tập Toán lớp 8 Bài 5: Diện tích hình thoi

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 127 Toán 8 Tập 1: Hãy tính diện tích tứ giác ABCD theo AC, BD, biết AC ⊥ BD tại H (h.145)

Lời giải

S_ABC = $\frac{1}{2}$BH.AC

S_ADC =  $\frac{1}{2}$DH.AC

S_ABCD = S_ABC +S_ADC 

=  $\frac{1}{2}$BH.AC + $\frac{1}{2}$DH.AC

= $\frac{1}{2}$(BH + DH).AC = $\frac{1}{2}$.BD.AC

Câu hỏi 2 trang 127 Toán 8 Tập 1:Hãy viết công thức tính diện tích hình thoi theo hai đường chéo.

Lời giải

Xét hình thoi ABCD, có hai đường chéo AC và BD vuông góc với nhau tại O.

Khi đó diện tích hình thoi ABCD bằng tổng diện tích tam giác ABC và diện tích tam giác ADC.

Diện tích tam giác ABC là: $S_{\Delta ABC}=\frac{1}{2}AC.BO$

Diện tích tam giác ADC là: $S_{\Delta ADC}=\frac{1}{2}AC.DO$

Diện tích hình thoi ABCD là: 

$$\begin{gathered} S_{ABCD}=S_{\Delta ABC}+S_{\Delta ADC} \\ =\frac{1}{2}AC.BO+\frac{1}{2}AC.DO \\ =\frac{1}{2}AC\left(BO+DO\right)=\frac{1}{2}AC.BD. \end{gathered}$$

Vậy diện tích hình thoi bằng một phần hai tích độ dài hai đường chéo.

Câu hỏi 3 trang 127 Toán 8 Tập 1: Hãy tính diện tích hình thoi bằng cách khác.

Lời giải

Cách 1: Hình thoi ABCD cũng là hình bình hành. Kẻ đường cao AH ứng với CD

⇒ S_ABCD = AH.CD

Cách 2: Tam giác ACD có đường cao DO ứng với cạnh AC

⇒ S_ACD = $\frac{1}{2}$.DO.AC

Do đó:

S_ABCD = 2S_ACD = 2.$\frac{1}{2}$.DO.AC

= $\frac{1}{2}$.(2DO).AC = $\frac{1}{2}$.BD.AC

(O là trung điểm BD nên BD = 2DO)

Bài tập (trang 127, 128)

Bài 32 trang 127 Toán 8 Tập 1: a) Hãy vẽ một tứ giác có độ dài hai đường chéo là: 3,6 cm, 6cm và hai đường chéo đó vuông góc với nhau. Có thể vẽ được bao nhiêu tứ giác như vậy? Hãy tính diện tích mỗi tứ giác vừa vẽ.

b) Hãy tính diện tích hình vuông có độ dài đường chéo là d.

Lời giải:

a)

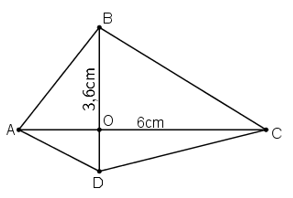
Có thể vẽ được vô số tứ giác theo yêu cầu từ đề bài. Chẳng hạn tứ giác ABCD ở hình trên.

Ta có: AC = 6cm, BD = 3,6cm và AC ⊥ BD tại O.

Diện tích tứ giác ABCD bằng diện tích tam giác ABD cộng với diện tích tam giác BCD bằng:

$$\begin{gathered} S_{ABCD}=S_{ABD}+S_{CBD} \\ =\frac{1}{2}AO.BD+\frac{1}{2}CO.BD \\ =\frac{1}{2}BD\left(AO+CO\right)=\frac{1}{2}BD.AC \end{gathered}$$

Mà AC = 6cm ; BD = 3,6 cm nên $S_{ABCD}=\frac{1}{2}\mathrm{.6.3},6=10,8\left(c{m}^2\right).$

Vậy diện tích tứ giác ABCD là 10,8 cm².

b) Hình vuông có 2 đường chéo vuông góc nên theo công thức trên, diện tích của nó là: $S=\frac{1}{2}d.d=\frac{1}{2}{d}^2.$

Bài 33 trang 127 Toán 8 Tập 1:Vẽ hình chữ nhật có một cạnh bằng đường chéo của một hình thoi cho trước và có diện tích bằng diện tích của hình thoi đó. Từ đó suy ra cách tính diện tích hình thoi.

Lời giải:

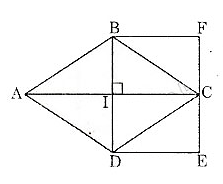
Cho hình thoi ABCD, vẽ hình chữ nhật có một cạnh là đường chéo BD,

Để diện tích của hình chữ nhật BDEF bằng diện tích hình thoi ABCD thì cạnh kia bằng IC (bằng nửa AC).

Thật vậy, diện tích hình chữ nhật BFED là

S_BFED = BD.BF = BD.IC

= BD.$\frac{1}{2}AC$=$\frac{1}{2}BD.AC.$

Diện tích hình thoi ABCD là: $S_{ABCD}=\frac{1}{2}BD.AC.$

$\Rightarrow S_{ABCD}=S_{BFED}.$

Từ đó suy ra cách tính diện tích hình thoi: Diện tích hình thoi bằng nửa tích hai đường chéo.

Bài 34 trang 127 Toán 8 Tập 1:Cho một hình chữ nhật. Vẽ tứ giác có các đỉnh là trung điểm các cạnh của hình chữ nhật. Vì sao tứ giác này là một hình thoi? So sánh diện tích hình chữ nhật, từ đó suy ra cách tính diện tích hình thoi.

Lời giải:

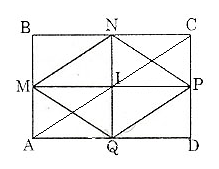
Vẽ hình chữ nhật ABCD với các trung điểm các cạnh AB, BC, CD, AD lần lượt là M, N, P, Q.

Vẽ tứ giác MNPQ

Xét tam giác ABC, có:

M là trung điểm của AB

N là trung điểm của BC

Suy ra MN là đường trung bình của tam giác ABC

$\Rightarrow MN=\frac{1}{2}AC$ và MN // AC (1)

Xét tam giác ADC, có:

P là trung điểm của DC

Q là trung điểm của AD

Suy ra PQ là đường trung bình của tam giác ADC

$\Rightarrow PQ=\frac{1}{2}AC$ và PQ // AC (2)

Từ (1) và (2) suy ra MN = PQ và MN // PQ

Tứ giác MNPQ có MN = PQ và MN // PQ nên MNPQ là hình bình hành.

Xét tam giác BDC, có:

N là trung điểm của BC

P là trung điểm của CD

Suy ra NP là đường trung bình của tam giác BDC

$\Rightarrow PN=\frac{1}{2}BD$ (3)

Mà ABCD là hình chữ nhật nên AC = BD (4)

Từ (1), (2) và (3) suy ra: MN = PN

Suy ra hình bình hành MNPQ có hai cạnh kề MN = PN nên MNPQ là hình thoi.

+ Ta có:

Diện tích hình thoi MNPQ là: $S_{MNPQ}=\frac{1}{2}MQ.NP$

Diện tích hình chữ nhật ABCD là: $S_{ABCD}=AB.BC$

Ta có ABCD là hình chữ nhật nên ABCD là hình thang, có:

M là trung điểm của AB

Q là trung điểm của CD

Suy ra MQ là đường trung bình của hình thang ABCD

$\Rightarrow MQ=\frac{1}{2}\left(AB+CD\right)=\frac{1}{2}\left(AB+AB\right)=AB$

Chứng minh tương tự NP = BC.

Do đó $S_{MNPQ}=\frac{1}{2}{S}_{ABCD}.$

Vậy diện tích hình thoi bằng nửa tích hai đường chéo.

Bài 35 trang 128 Toán 8 Tập 1:Tính diện tích hình thoi có cạnh dài 6cm và một trong các góc của nó có số đo là 60^o.

Lời giải

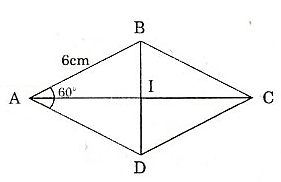
Cho hình thoi ABCD có cạnh AB = 6cm, góc $\widehat{A}$ = 60^o.

- Cách 1:

Xét ΔABD có AB = AD (ABCD là hình thoi)

Suy ra ΔABD là tam giác cân

Mà $\widehat{A}$ = 60^o nên ΔABD đều

Do đó BD = AB = 6cm

Gọi I là giao điểm của AC và BD $\Rightarrow$ AC ⊥ DB tại I và I là trung điểm của AC và là trung điểm của BD.

Suy ra IB = ID = $\frac{BD}{2}=\frac{6}{2}=3cm.$

Xét tam giác ABI vuông tại I, có:

$A{B}^2=A{I}^2+I{B}^2$ (định lý Py – ta – go)

$\begin{array}{l}\Rightarrow 6^2=A{I}^2+3^2\\ \Rightarrow A{I}^2=6^2-3^2\\ \Rightarrow A{I}^2=27\\ \Rightarrow AI=3\sqrt{3}\\ \Rightarrow AC=2AI=2.3\sqrt{3}=6\sqrt{3}cm\end{array}$

Diện tích hình thoi ABCD là:

$$\begin{gathered} S_{ABCD}=\frac{1}{2}AC.BD \\ =\frac{1}{2}.6\sqrt{3}.6=18\sqrt{3}\left(c{m}^2\right). \end{gathered}$$

Vậy diện tích hình thoi ABCD là $18\sqrt{3}c{m}^2.$

- Cách 2:

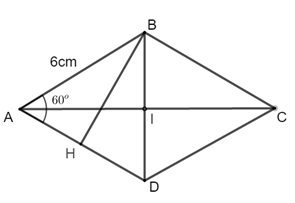
Vì ΔABD là tam giác đều (cmt).

Từ B vẽ BH ⊥ AD thì HA = HD = $\frac{AD}{2}=\frac{6}{2}=3cm.$

Xét tam giác ABH vuông tại H, có:

$A{B}^2=A{H}^2+H{B}^2$ (định lý Py – ta – go)

$\begin{array}{l}\Rightarrow 6^2=B{H}^2+3^2\\ \Rightarrow B{H}^2=6^2-3^2\\ \Rightarrow B{H}^2=27\\ \Rightarrow BH=3\sqrt{3}\end{array}$

Diện tích hình thoi ABCD là: 

$$\begin{gathered} S_{ABCD}=AD.BH \\ =6.3\sqrt{3}=18\sqrt{3}\left(c{m}^2\right). \end{gathered}$$

Vậy diện tích hình thoi ABCD là $18\sqrt{3}c{m}^2.$

Bài 36 trang 128 Toán 8 Tập 1:Cho một hình thoi và một hình vuông có cùng chu vi. Hỏi hình nào có diện tích lớn hơn? Vì sao?

Lời giải:

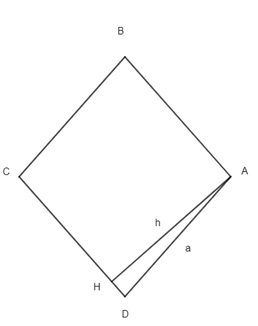
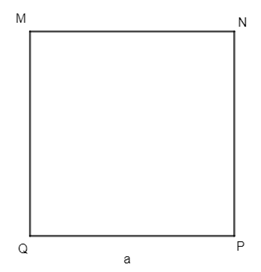
Giả sử hình thoi ABCD và hình vuông MNPQ có cùng chu vi là 4a

Suy ra cạnh hình thoi và cạnh hình vuông đều có độ dài a

Diện tích hình vuông MNPQ là: S_MNPQ = a² (đvdt)

Từ đỉnh góc từ A của hình thoi ABCD, vẽ đường cao AH ứng với cạnh CD có độ dài là h.

Vì ABCD là hình thoi nên ABCD là hình bình hành

⇒ Diện tích hình thoi ABCD là: S_ABCD = ah

Xét tam giác AHB vuông tại H, ta có:

AH  AB hay h ≤ a (đường vuông góc nhỏ hơn đường xiên)

⇒ ah ≤ a² 

⇒ S_ABCD ≤ S_MNPQ

Vậy diện tích hình vuông luôn lớn hơn hoặc bằng diện tích hình thoi.