Với giải bài 20 trang 122 Toán lớp 8 chi tiết trong Bài 3: Diện tích tam giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:
Giải bài tập Toán lớp 8 Bài 3: Diện tích tam giác
Bài 20 trang 122 Toán 8 Tập 1:Vẽ hình chữ nhật có một cạnh bằng cạnh của một tam giác cho trước và có diện tích bằng diện tích của tam giác đó. Từ đó suy ra một cách chứng minh khác về công thức tính diện tích tam giác.
Lời giải:
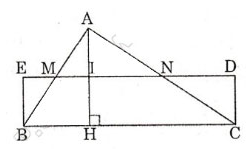
Cho ΔABC với đường cao AH.
Gọi M, N, I là trung điểm của AB, AC, AH.
Lấy E đối xứng với I qua M, D đối xứng với I qua N.
⇒ Hình chữ nhật BEDC là hình cần dựng.
Thật vậy:
Xét ΔEBM và ΔIAM, có:
ME = MI (E đối xứng với I qua M)
(hai góc đối đỉnh)
AM = MB (M là trung điểm của AB)
Suy ra ΔEBM = ΔIAM
Chứng minh tương tự ΔDCN = ΔIAN
⇒ SEBM = SAMI và SCND = SAIN
⇒ SABC = SAMI + SAIN + SBMNC
= SEBM + SBMNC + SCND = SBCDE.
Suy ra SABC = SBCDE = BE.BC
= AH.BC. (Vì BE = IA = ).
Ta đã tìm lại công thức tính diện tích tam giác bằng một phương pháp khác
Xem thêm lời giải bài tập Toán lớp 8 hay, chi tiết khác:
Bài 22 trang 122 Toán 8 Tập 1:Tam giác PAF được vẽ trên giấy kẻ ô vuông (h.135). Hãy chỉ ra:...
Bài 25 trang 123 Toán 8 Tập 1:Tính diện tích của một tam giác đều có cạnh bằng a...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
