Tailieumoi.vn xin giới thiệu Bài tập Toán 8 Chương 2 Bài 3: Diện tích tam giác. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 2 Bài 3:Diện tích tam giác. Mời các bạn đón xem:

Bài tập Toán 8 Chương 2 Bài 3: Diện tích tam giác

A. Bài tập Diện tích tam giác

I. Bài tập trắc nghiệm

Bài 1: Cho Δ ABC, có đường cao AH = $\frac{2}{3}$BC thì diện tích tam giác là ?

A. $\frac{2}{5}$BC².   

B. $\frac{2}{3}$BC².

C. $\frac{1}{3}$BC².  

D. $\frac{1}{3}$BC.

Lời giải:

Ta có diện tích của tam giác: S = $\frac{1}{2}$b.h.

Trong đó: b là độ dài cạnh đáy, h là độ dài đường cao

Khi đó ta có : S = $\frac{1}{2}$AH.BC = $\frac{1}{2}$.$\frac{2}{3}$BC.BC = $\frac{1}{3}$BC².

Chọn đáp án C.

Bài 2: Δ ABC có đáy BC = 6cm, đường cao AH = 4cm. Diện tích Δ ABC là ?

A. 24cm²   

B. 12cm²

C. 24cm.   

D. 14cm²

Lời giải:

Ta có diện tích Δ ABC là S = $\frac{1}{2}$AH.BC = $\frac{1}{2}$.6.4 = 12( cm² ).

Chọn đáp án B.

Bài 3: Cho Δ ABC vuông tại A, có đáy BC = 5cm và AB = 4cm. Diện tích Δ ABC là ?

A. 12cm²   

B. 10cm

C. 6cm²   

D. 3cm²

Lời giải:

Áp dụng định lý Py – to – go ta có: AB² + AC² = BC² ⇒ AC = $\sqrt{\left(B{C}^2-A{B}^2\right)}$

⇒ AC = $\sqrt{5^2-4^2}$ = 3cm.

Khi đó S_ABC = $\frac{1}{2}$AB.AC = $\frac{1}{2}$.4.3 = 6( cm² )

Chọn đáp án C.

Bài 4: Cho Δ ABC, đường cao AH. Biết AB = 15cm, AC = 41cm, HB = 12cm. Diện tích của Δ ABC là ?

A. 234 (cm²)   

B. 214 (cm²)

C. 200 (cm²)   

D. 154 (cm²)

Lời giải:

Áp dụng định lý Py – to – go ta có:

+ Xét Δ ABH có AH² + BH² = AB² ⇒ AH = $\sqrt{(A{B}^2 - B{H}^2)}$

⇒ AH = $\sqrt{({15}^2 - {12}^2)}$ = 9 ( cm ).

+ Xét Δ ACH có AC² = AH² + HC² ⇒ HC = $\sqrt{(A{C}^2 - A{H}^2)}$

⇒ HC = $\sqrt{({41}^2 - 9^2)}$ = 40 ( cm ).

Khi đó S_ABC = $\frac{1}{2}$AH.BC = $\frac{1}{2}$AH( HB + HC ) = $\frac{1}{2}$.9.( 12 + 40 ) = 234 ( cm² ).

Chọn đáp án A.

Bài 5: Cho tam giác ABC có AB = 6cm, AC = 8cm. Hai đường cao xuất phát từ đỉnh B và C là BH và CK. Biết BH = 9cm. Tính CK

A. 12cm    

B. 15cm

C. 9cm    

D. 8cm

Lời giải:

Diện tích tam giác ABC là:

Suy ra: 3CK = 36 nên CK = 12cm

Chọn đáp án A

Bài 6: Cho tam giác ABC vuông tại A có AB = 6cm; AC = 8 cm. Tính độ dài đường cao xuất phát từ A?

A. 4cm    

B. 4,5cm

C. 4,8cm    

D. 5cm

Lời giải:

Áp dụng định lí Pytago vào tam giác ABC ta có:

BC² = AB² + AC² = 6² + 8² = 100

Suy ra: BC = 10cm

Diện tích tam giác ABC là:

Gọi AH là đường cao xuất phát từ đỉnh A của tam giác ABC ,

Khi đó:

Suy ra: 5AH = 24 ⇔ AH = 4,8cm

Chọn đáp án C

Bài 7: Cho tam giác ABC có đường cao AH = 6cm, diện tích tam giác ABC là 30 cm². Gọi M là trung điểm của BC. Tính diện tích tam giác ABM

A. 10cm²    

B. 12cm²

C. 20cm²    

D. 15cm²

Lời giải:

Chọn đáp án D

Bài 8: Cho tam giác ABC có diện tích bằng 40cm². Gọi M là trung điểm của AC . Tính diện tích tam giác ABM?

A. 10cm²    

B. 20cm²

C. 25cm²    

D. Chưa thể kết luận

Lời giải:

Chọn đáp án B

Bài 9: Cho tam giác ABC có AB = 4cm và AC = 7cm. Gọi BH và CK theo thứ tự là đường vuông góc từ đỉnh B và C của tam giác. Tính $\frac{BH}{CK}$ ?

A. $\frac{4}{7}$     

B. $\frac{7}{4}$

C. $\frac{4}{3}$    

D. Đáp án khác

Lời giải:

Chọn đáp án A

Bài 10: Cho tam giác ABC có AB = 6cm và AC = 8cm . Gọi M và N theo thứ tự là trung điểm của AC và AB. Tính tỉ số 

A. $\frac{1}{2}$    

B. 2

C. 1    

D. Chưa thể kết luận

Lời giải:

Chọn đáp án C

II. Bài tập tự luận có lời giải

Bài 1: Giải thích vì sao diện tích của tam giác được tô đậm trong hình 128, 129, 130 bằng nửa diện tích hình chữ nhật tương ứng.

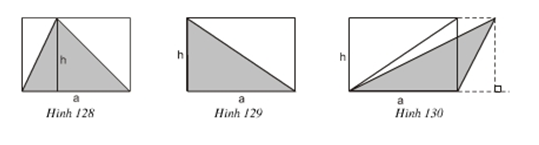
Lời giải:

Trong mỗi hình trên ta đều có:

Diện tích hình chữ nhật là: a.h

⇒ Diện tích của tam giác bằng nửa diện tích hình chữ nhật tương ứng.

Bài 2 Cho tam giác ABC và đường trung tuyến AM (h.132). Chứng minh: S_AMB = S_AMC

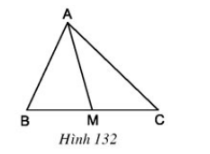
Lời giải:

Kẻ đường cao AH.

Ta có:

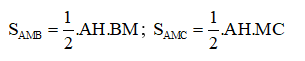
Mà BM = CM (vì AM là trung tuyến)

⇒ S_AMB = S_AMC (đpcm).

Bài 3

a) Xem hình 133. Hãy chỉ ra các tam giác có cùng diện tích (lấy ô vuông làm đơn vị diện tích)

b) Hai tam giác có diện tích bằng nhau thì có bằng nhau hay không?

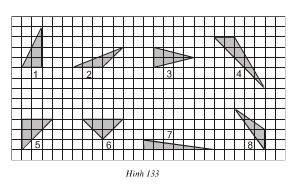
Lời giải:

a) Các tam giác số 1, 3, 6 có cùng diện tích là 4 ô vuông

Các tam giác số 2, 8 có cùng diện tích là 3 ô vuông.

Các tam giác số 4, 5, 7 không có cùng diện tích với các tam giác nào khác (diện tích tam giác số 4 là 5 ô vuông, tam giác số 5 là 4, 5 ô vuông, tam giác số 7 là 3,5 ô vuông).

b) Hai tam giác có diện tích bằng nhau thì không nhất thiết bằng nhau.

Vì diện tích của tam giác là 1 nửa tích của độ dài đáy với chiều cao tương ứng của đáy, nên chỉ cần tích của đáy với chiều cao bằng nhau thì 2 tam giác đó có diện tích bằng nhau, 2 cạnh còn lại có thể khác nhau.

Bài 4 Tam giác PAF được vẽ trên giấy kẻ ô vuông (h.135). Hãy chỉ ra:

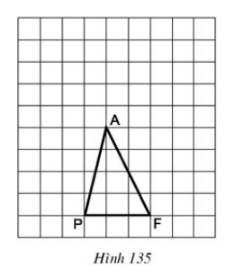
a) Một điểm I sao cho S_PIF= S_PAF

b) Một điểm O sao cho S_POF= 2.S_PAF

c) Một điểm N sao cho:

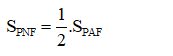
Lời giải:

Gọi AH là chiều cao của tam giác APF.

Ta có: S_APF = $\frac{AH.PF}{2}$.

a) S_PIF= S_PAF

⇔ chiều cao IK = AH (Chung cạnh đáy PF).

⇔ I nằm trên đường thẳng song song với PF và cách PF 1 khoảng bằng AH.

b) S_POF= 2.S_PAF

⇔ chiều cao OM = 2.AH

⇔ O nằm trên đường thẳng song song với PF và cách PF một khoảng bằng 2.AH

c)

⇔ chiều cao NQ = $\frac{AH}{2}$

⇔ N nằm trên đường thẳng song song với PF và cách PF một khoảng bằng AH/2.

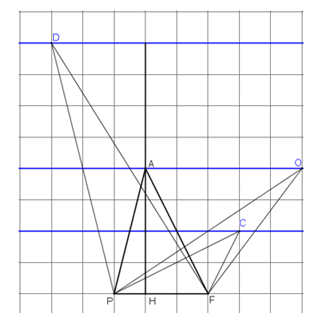
Bài 4 Tam giác PAF được vẽ trên giấy kẻ ô vuông (h.135). Hãy chỉ ra:

a) Một điểm I sao cho S_PIF = S_PAF

b) Một điểm O sao cho S_POF = 2.S_PAF

c) Một điểm N sao cho 

Lời giải:

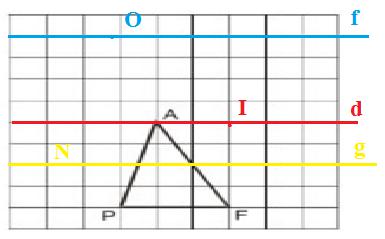
Cho ΔPAF vẽ trên giấy kẻ ô vuông như trên hình.

a) Nếu lấy điểm I bất kì nằm trên đường thẳng d đi qua A và song song với đường thẳng PF thì S_PIF = S_PAF

(cùng bằng nửa tích khoảng cách từ A (hoặc I) đến PF nhân với độ dài của PF)

b) Nếu lấy một điểm O sao cho khoảng cách từ O đến đường thẳng PF bằng hai lần khoảng cách từ A đến đường thẳng PF thì S_POF = 2S_PAF.

Có vô số điểm O như thế (ví dụ O nằm trên đường thẳng f như trên hình).

c) Nếu lấy điểm N sao cho khoảng cách từ N đến đường thẳng PF

Có vô số điểm N như thế nằm trên hai đường thẳng song song với đường thẳng PF (ví dụ đường thẳng g).

Bài 5 Cho tam giác ABC. Hãy chỉ ra một số vị trí của điểm M nằm trong tam giác đó sao cho: S_AMB + S_BMC = S_MAC

Lời giải:

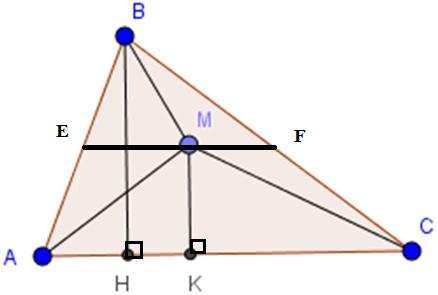
Kẻ đường cao BH, MK.

Theo giả thiết, M là điểm nằm trong tam giác ABC sao cho:

S_AMB + S_BMC = S_MAC

Ta lại có: S_AMB + S_BMC + S_MAC = S_ABC

Suy ra: S_MAC = $\frac{1}{2}$ S_ABC

⇒ $\frac{1}{2}$ MK.AC = $\frac{1}{2}$ ($\frac{1}{2}$ BH.AC)

⇒ MK = $\frac{1}{2}$ BH

Do đó, M nằm trên đường thẳng sao cho khoảng cách từ M đến BC = $\frac{1}{2}$ đường cao BH.

Vậy điểm M nằm trên đường trung bình của ΔABC

Bài 6 Tính diện tích của một tam giác cân có cạnh đáy bằng a và cạnh bên bằng b.

Lời giải:

Gọi h là chiều cao của tam giác cân.

Theo định lí Pitago ta có:

Bài 7 Tính diện tích của một tam giác đều có cạnh bằng a.

Lời giải:

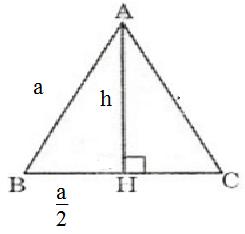
Gọi h là chiều cao của tam giác đều cạnh a.

Theo định lí Pitago ta có:

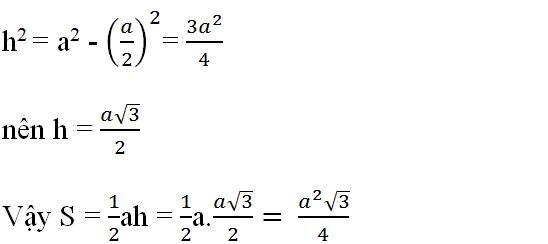
Bài 8 Tính x sao cho diện tích hình chữ nhật. ABCD gấp ba lần diện tích tam giác ADE (h.134).

Lời giải:

Ta có AD = BC = 5cm

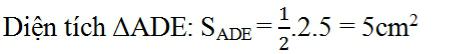
Diện tích hình chữ nhật ABCD: S_ABCD = 5x

Theo đề bài ta có S_ABCD = 3S_ADE nên 5x = 3.5

Vậy x = 3cm

III. Bài tập vận dụng

Bài 1 Cho tam giác ABC có diện tích 150cm². M là trung điểm của BC, N là trung điểm của AC. Nối MN. Tính diện tích tam giác CMN ?

Bài 2 Cho hình vẽ. Tính tỉ số diện tích 2 tam giác BDF và AEF ?

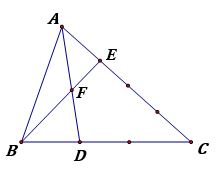
Bài 3 Cho hình chữ nhật ABCD, F là một điểm bất kì trên cạnh AD, BF cắt CD kéo dài tại điểm E. Nối điểm A với điểm E. Tính diện tích tam giác AEF, biết AF = 3cm, BC = 5cm, AB = 7 cm ?

Bài 4 Cho tam giác ABC biết BM = MC; CN = 3 x NA (như hình vẽ) và diện tích tam giác AEN bằng 27 cm².Tính diện tích tam giác ABC ?

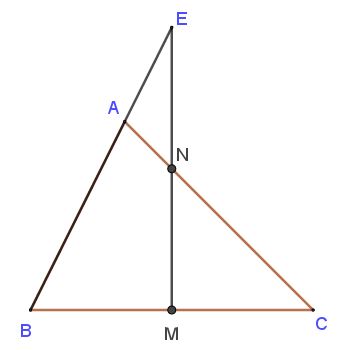
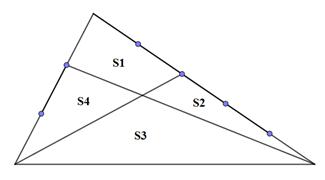
Bài 5 Cho hình vẽ bên biết S1 = 12cm². Tính S2

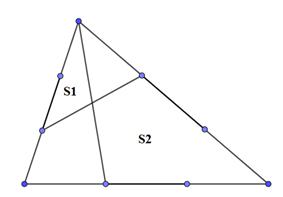
Bài 6 Cho tam giác với các tỷ lệ như hình.

Biết S3−S1=84cm². Tính S4−S2

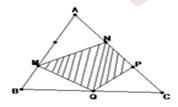
Bài 7 Cho tam giác ABC có diện tích là 180 cm2. Biết AB = 3 x BM; AN = NP=PC; QB=QC. Tính diện tích tam giác MNPQ ? (xem hình vẽ)

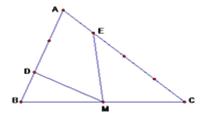
Bài 8 Cho tam giác ABC có diện tích bằng 18cm². Biết DA = 2 x DB ; EC = 3 x EA ; MC = MB (hình vẽ). Tính tổng diện tích hai tam giác MDB và MCE ?

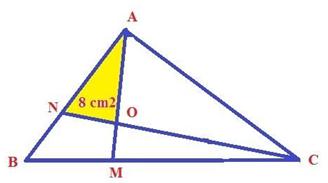
Bài 9 Trong hình vẽ bên có NA = 2 x NB; MC = 2 x MB và diện tích tam giác OAN là 8cm². Tính diện tích BNOM ?

Bài 10 Cho tam giác ABC và các điểm D, E, G, H sao cho BD = $\frac{1}{3}$x AB; AE = CG = $\frac{1}{3}$ x AC; CH =$\frac{1}{3}$x BC. Tính diện tích hình BDEGH ? ( Biết diện tích của tam giác ABC là 180cm² )

B. Lý thuyết Diện tích tam giác

1. Khái niệm diện tích đa giác

• Số đo của phần mặt phẳng giới hạn bởi một đa giác được gọi là diện tích đa giác đó.

• Mỗi đa giác có một diện tích xác định. Diện tích đa giác là một số dương.

• Diện tích đa giác có các tính chất sau:

- Hai tam giác bằng nhau thì có diện tích bằng nhau.

- Nếu một đa giác được chia thành những đa giác không có điểm trong chung thì diện tích của nó bằng tổng diện tích của những đa giác đó.

- Nếu chọn hình vuông có cạnh bằng 1 cm, 1 dm, 1 m, . . . làm đơn vị đo diện tích thì đơn vị diện tích tương ứng là $1c{m}^2,1d{m}^2,1m^2$ . . .

2. Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông.

.

 

 

 

 

 

$S=\frac{1}{2}a.b$

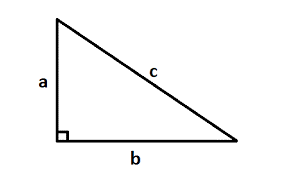3. Diện tích tam giác

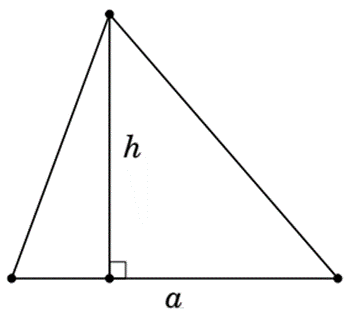
Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng vớicạnh đó.

$S=\frac{1}{2}a.b$