Với giải bài 55 trang 96 Toán lớp 8 chi tiết trong Bài 8: Đối xứng tâm giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:
Giải bài tập Toán lớp 8 Bài 8: Đối xứng tâm
Bài 55 trang 96 Toán 8 Tập 1: Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt các cạnh AB và CD theo thứ tự ở M và N. Chứng minh rằng điểm M đối xứng với điểm N qua O.
Lời giải:
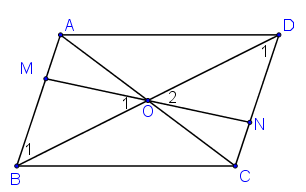
+ ABCD là hình bình hành có O là giao điểm hai đường chéo
⇒ OB = OD.
Vì ABCD là hình bình hành ⇒ AB // CD ⇒ (Hai góc SLT).
Xét và có:
(cmt)
OB = OD
(hai góc đối đỉnh)
⇒ ΔBOM = ΔDON (g.c.g)
⇒ OM = ON
⇒ O là trung điểm của MN
Vậy M đối xứng với N qua O.
Xem thêm lời giải bài tập Toán lớp 8 hay, chi tiết khác:
Câu hỏi 2 trang 94 Toán 8 Tập 1:Cho điểm O và đoạn thẳng AB (h.75)...
Bài 56 trang 96 Toán 8 Tập 1: Trong các hình sau, hình nào có tâm đối xứng?...
Bài 57 trang 96 Toán 8 Tập 1: Các câu sau đúng hay sai?...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
