Tailieumoi.vn xin giới thiệu Giải bài tập Toán 8 Bài 8: Đối xứng tâm hay, chi tiết giúp học sinh dễ dàng làm bài tập Đối xứng tâm lớp 8.

Giải bài tập Toán lớp 8 Bài 8: Đối xứng tâm

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 93 Toán 8 Tập 1: Cho điểm O và điểm A. Hãy vẽ điểm A’ sao cho O là trung điểm của đoạn thẳng AA’.

Lời giải

Trên tia đối tia OA lấy điểm A’ sao cho OA’ = OA, ta được:

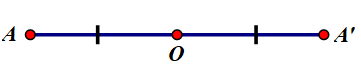
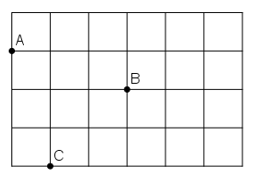
Câu hỏi 2 trang 94 Toán 8 Tập 1:Cho điểm O và đoạn thẳng AB (h.75)

- Vẽ điểm A’ đối xứng với A qua O.

- Vẽ điểm B’ đối xứng với B qua O.

- Lấy điểm C thuộc đoạn thẳng AB, vẽ điểm C’ đối xứng với C qua O.

- Dùng thước để kiểm nghiệm rằng điểm C’ thuộc đoạn thẳng A’B’.

Lời giải

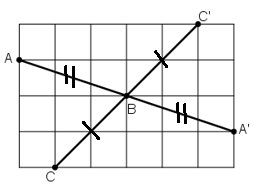
- Vẽ điểm A’ đối xứng với A qua O:

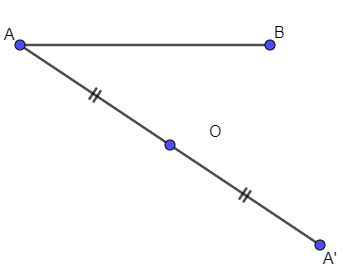
- Vẽ điểm B’ đối xứng với B qua O:

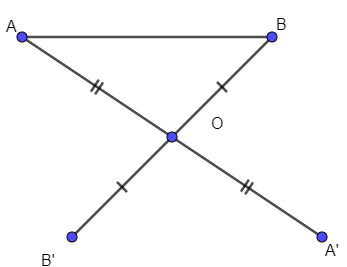
- Lấy điểm C thuộc đoạn thẳng AB, vẽ điểm C’ đối xứng với C qua O:

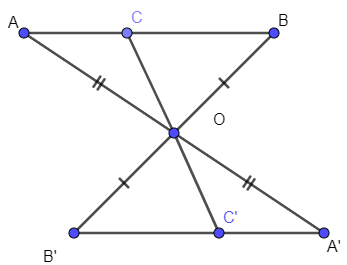
- Dùng thước để kiểm nghiệm rằng điểm C’ thuộc đoạn thẳng A’B’:

Đặt thước vào đoạn A’B’ ta thấy C’ cũng nằm trên đoạn thẳng đó.

Vậy điểm C’ thuộc đoạn thẳng A’B

Câu hỏi 3 trang 95 Toán 8 Tập 1: Gọi O là giao điểm hai đường chéo của hình bình hành ABCD (h.79). Tìm hình đối xứng với mỗi cạnh của hình bình hành qua điểm O.

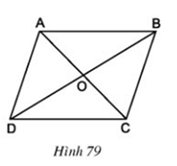
Lời giải

Vì ABCD là hình bình hành nên O là trung điểm của AC vừa là trung điểm của BD. Do đó, ta có:

C đối xứng với A qua O

B đối xứng với D qua O

Suy ra AB đối xứng với CD qua O

Và AD đối xứng với CB qua O

Câu hỏi 4 trang 95 Toán 8 Tập 1: Trên hình 80, các chữ cái N và S có tâm đối xứng, chữ cái E không có tâm đối xứng. Hãy tìm thêm một vài chữ cái khác (kiểu chữ in hoa) có tâm đối xứng.

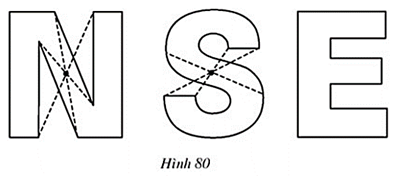
Lời giải

Một vài chữ khác có tâm đối xứng là: H, I, X.

Bài tập (trang 95, 96)

Bài 50 trang 95 Toán 8 Tập 1: Vẽ điểm A' đối xứng với A qua B, vẽ điểm C' đối xứng với C qua B (h.81)

Hình 81

Lời giải

Bài 51 trang 96 Toán 8 Tập 1: Trong mặt phẳng tọa độ, cho điểm H có tọa độ (3; 2). Hãy vẽ điểm K đối xứng với H qua gốc tọa độ và tìm tọa độ của K.

Lời giải

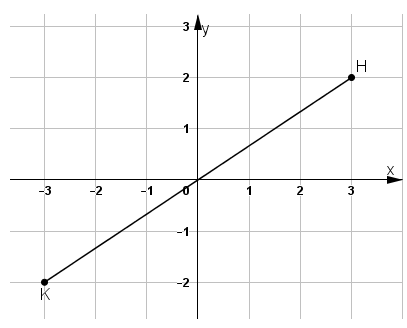
K đối xứng với H qua gốc tọa độ

⇔ O(0; 0) là trung điểm của KH.

Dựa vào hình biểu diễn ta có K(-3; -2).

Bài 52 trang 96 Toán 8 Tập 1: Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua điểm A, gọi F là điểm đối xứng với D qua C. Chứng minh rằng E đối xứng với điểm F qua điểm B.

Lời giải:

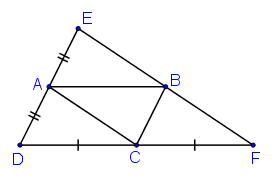
Ta có: ABCD là hình bình hành nên:

AD//BC, AD = BC

Mà AE = AD (E đối xứng với D qua A)

⇒ BC = AE.

Xét tứ giác AEBC có BC // AE, BC = AE nên AEBC là hình bình hành

⇒ EB // AC và EB = AC (1).

Xét tam giác DEF, có:

A là trung điểm DE ( D và E đối xứng qua A)

C là trung điểm của DF ( D và F đối xứng qua C)

AC là đường trung bình của tam giác DEF

⇒ AC // EF, AC = $\frac{1}{2}$EF (2)

Từ (1) và (2) suy ra E, B, F thẳng hàng và BE = BF

⇒ B là trung điểm EF

⇒ E đối xứng với F qua B

Bài 53 trang 96 Toán 8 Tập 1: Cho hình 82, trong đó MD // AB và ME // AC. Chứng minh rằng điểm A đối xứng với điểm M qua điểm I.

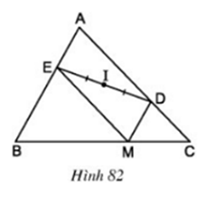
Lời giải:

Xét tứ giác MDAE, ta có:

MD// AE (vì MD// AB)

ME // AD (vì ME // AC)

Nên AEMD là hình bình hành

Mà I là trung điểm của DE nên I cũng là trung điểm của AM

Do đó A đối xứng với M qua I.

Bài 54 trang 96 Toán 8 Tập 1: Cho góc vuông xOy, điểm A nằm trong góc đó. Gọi B là điểm đối xứng với A qua Ox, gọi C là điểm đối xứng với A qua Oy. Chứng minh rằng điểm B đối xứng với điểm C qua O.

Lời giải:

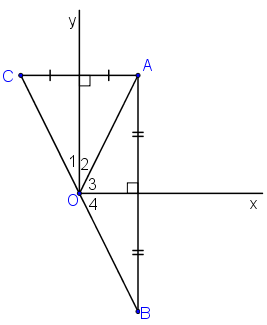
+ B đối xứng với A qua Ox

⇒ Ox là đường trung trực của AB

⇒ OA = OB (1)

+ C đối xứng với A qua Oy

⇒ Oy là đường trung trực của AC

⇒ OA = OC (2)

Từ (1) và (2) suy ra OB = OC (*).

+ Xét ΔOAC cân tại O (do OA = OC) có Oy là đường trung trực

⇒ Oy đồng thời là đường phân giác

$\Rightarrow \widehat{O_1}=\widehat{O_2}$(3)

Xét ΔOAB cân tại O có Ox là đường trung trực

⇒ Ox đồng thời là đường phân giác

$\Rightarrow \widehat{O_3}=\widehat{O_4}$(4)

Từ (3) và (4) suy ra:$\widehat{O_1}+\widehat{O_4}=\widehat{O_2}+\widehat{O_3}$

Mà $\widehat{O_2}+\widehat{O_3}=\widehat{xOy}={90}^0$

$\begin{array}{l}\Rightarrow \widehat{O_1}+\widehat{O_4}=\widehat{O_2}+\widehat{O_3}={90}^0\\ \Rightarrow \widehat{O_1}+\widehat{O_4}+\widehat{O_2}+\widehat{O_3}={90}^0+{90}^0={180}^0\\ \Rightarrow \widehat{BOC}={180}^0\end{array}$

⇒ B, O, C thẳng hàng (**)

Từ (*) và (**) suy ra O là trung điểm BC

⇒ B đối xứng với C qua O.

Bài 55 trang 96 Toán 8 Tập 1: Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt các cạnh AB và CD theo thứ tự ở M và N. Chứng minh rằng điểm M đối xứng với điểm N qua O.

Lời giải:

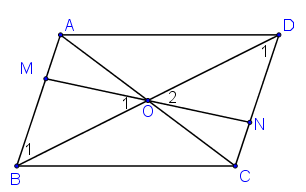
+ ABCD là hình bình hành có O là giao điểm hai đường chéo

⇒ OB = OD.

Vì ABCD là hình bình hành ⇒ AB // CD ⇒ $\widehat{B_1}=\widehat{D_1}$ (Hai góc SLT).

Xét $\Delta BOM$ và $\Delta DON$ có:

$\widehat{B_1}=\widehat{D_1}$(cmt)

OB = OD

$\widehat{BOM}=\widehat{DON}$ (hai góc đối đỉnh)

⇒ ΔBOM = ΔDON (g.c.g)

⇒ OM = ON

⇒ O là trung điểm của MN

Vậy M đối xứng với N qua O.

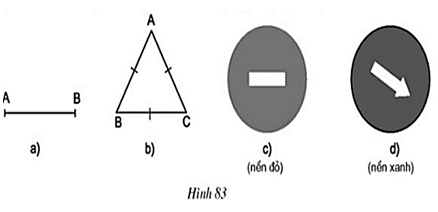
Bài 56 trang 96 Toán 8 Tập 1: Trong các hình sau, hình nào có tâm đối xứng?

a) Đoạn thẳng AB (h.83a)

b) Tam giác đều ABC (h.83b)

c) Biển cấm đi ngược chiều (h.83c)

d) Biển chỉ hướng đi vòng tránh chướng ngại vật (h.83d)

Lời giải:

- Hình 83a có tâm đối xứng là trung điểm của đoạn thẳng AB

- Hình 83b không có tâm đối xứng

(Lưu ý: Trọng tâm đồng thời là trực tâm của tam giác đều ABC không phải tâm đối xứng của tam giác đó)

- Hình 83c có tâm đối xứng là tâm của hình tròn.

- Hình 83d không có tâm đối xứng.

Bài 57 trang 96 Toán 8 Tập 1: Các câu sau đúng hay sai?

a) Tâm đối xứng của một đường thẳng là điểm bất kì của đường thẳng đó.

b) Trọng tâm của một tam giác là tâm đối xứng của tam giác đó.

c) Hai tam giác đối xứng với nhau qua một điểm thì có chu vi bằng nhau.

Lời giải:

a) Đúng, vì nếu lấy một điểm O bất kì trên đường thẳng thì nó chia đường thẳng đó thành hai và với bất kì một điểm M, trên tia này cũng luôn có một điểm M' đối xứng với nó qua O trên tia kia.

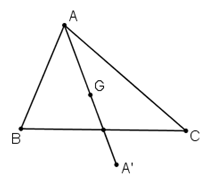
b) Sai,

Giả sử tam giác ABC có trọng tâm G.

Khi đó điểm A’ đối xứng với A qua G không nằm trong tam giác.

c) Đúng, vì hai tam giác đối xứng với nhau qua một điểm thì chúng bằng nhau.