Tailieumoi.vn xin giới thiệu Giải bài tập Toán 8 Bài 8: Các trường hợp đồng dạng của tam giác vuông hay, chi tiết giúp học sinh dễ dàng làm bài tập Các trường hợp đồng dạng của tam giác vuông lớp 8.

Giải bài tập Toán lớp 8 Bài 8: Các trường hợp đồng dạng của tam giác vuông

Trả lời câu hỏi giữa bài

Câu hỏi trang 81 Toán 8 Tập 2: Hãy chỉ ra các cặp tam giác đồng dạng trong hình 47.

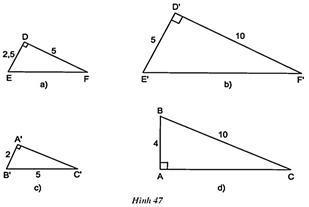
Lời giải:

+ ΔDEF vuông tại D và ΔD'E'F' vuông tại D’ có:

$$\begin{gathered} \frac{DE}{D\text{'}E\text{'}}=\frac{DF}{D\text{'}F\text{'}}=\frac{1}{2} \\ \widehat{D}=\widehat{D\text{'}}=90° \end{gathered}$$

⇒ ΔDEF $~$ ΔD'E'F'  (c – g – c)

*) Áp dụng định lí Py – ta - go vào tam giác A’B’C’ vuông tại A’ có:

A’C’² + A’B’² = B’C’²

Thay số:  A’C’² + 2² = 5²

Suy ra: A’C’² = 25 – 4 = 21 nên $A\text{'}C\text{'}=\sqrt{21}$

*) Áp dụng định lí Py – ta - go vào tam giác ABC vuông tại A có:

AB² + AC² = BC²

Thay số: 4² + AC² = 10²

Suy ra: AC² = 100 – 16 = 84 nên $AC=2\sqrt{21}$

+ Xét ∆A’B’C’ vuông tại A’ và ∆ABC vuông tại A có:

$$\begin{gathered} \widehat{A}=\widehat{A\text{'}}={90}^0 \\ \frac{A\text{'}B\text{'}}{AB}=\frac{A\text{'}C\text{'}}{AC}=\frac{1}{2} \end{gathered}$$

Do đó, ∆ A’B’C’ đồng dạng với tam giác ABC (c – g – c)

Bài tập (trang 84; 85)

Bài 46 trang 84 Toán 8 Tập 2: Trên hình 50 hãy chỉ ra các tam giác đồng dạng. Viết các tam giác này theo thứ tự các đỉnh tương ứng và giải thích vì sao chúng đồng dạng?

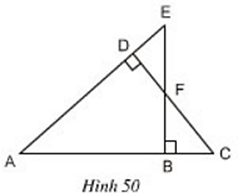
Lời giải:

Xét ∆ABE và ∆ADC có:

$\widehat{A}$chung

$\widehat{ABE}=\widehat{ADC}={90}^0$

Do đó,  ∆ABE $~$ ∆ADC (g - g)    (1).

+ Xét ∆FDE và ∆FBC có:

$\widehat{DFE}=\widehat{BFC}$( 2 góc đối đỉnh).

$\widehat{EDF}=\widehat{CBF}={90}^0$

Do đó, ∆FDE $~$ ∆FBC (g – g)(2).

+ Xét ∆ABE và ∆FDE có:

$\widehat{E}$chung

$\widehat{ABE}=\widehat{FDE}={90}^0$

Suy ra: ∆ABE $~$ ∆FDE (g – g) (3).

Từ (1) và (3) suy ra: ∆ADC $~$ ∆FDE  ( 4)

Từ (2) và (3) suy ra: ∆ABE  $~$  ∆FBC ( 5).

Từ (2) và (4) suy ra: ∆ADC $~$ ∆FBC   ( 6).

Vậy có tất cả 6 cặp tam giác đồng dạng.

Bài 47 trang 84 Toán 8 Tập 2: Tam giác ABC có độ dài các cạnh là 3cm, 4cm, 5cm. Tam giác A'B'C' đồng dạng với tam giác ABC và có diện tích là 54cm². Tính độ dài các cạnh của tam giác A'B'C'.

Lời giải:

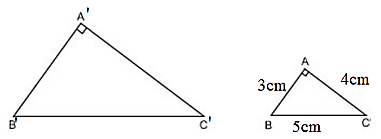
Xét ΔABC có:

AB² + AC² = 3² + 4² = 25 = 5² = BC²

⇒ ΔABC vuông tại A (Định lý Py – ta - go đảo)

⇒ Diện tích tam giác ABC là: $S=\frac{1}{2}AB.AC=6$ (cm²)

Theo giả thiết tam giác A'B'C' đồng dạng với tam giác ABC suy ra:

$\frac{A\text{'}B\text{'}}{AB}=\frac{B\text{'}C\text{'}}{BC}=\frac{C\text{'}A\text{'}}{CA}=k$

(với k là tỉ số đồng dạng).

Lại có tỉ số diện tích bằng bình phương tỉ số đồng dạng

$\Rightarrow k^2=\frac{S_{A\text{'}B\text{'}C\text{'}}}{S_{ABC}}=\frac{54}{6}=9\Rightarrow k=3$

⇒ A’B’ = 3.AB = 3.3 = 9 (cm)

B’C’ = 3.BC = 3.5 = 15 (cm)

C’A’ = 3.CA = 3.4 = 12 (cm)

Vậy độ dài ba cạnh của tam giác A’B’C’ lần lượt là 9cm, 12cm, 15cm.

Bài 48 trang 84 Toán 8 Tập 2: Bóng của cột điện trên mặt đất có độ dài là 4,5m. Cùng thời điểm đó, một thanh sắt cao 2,1m cắm vuông góc với mặt đất có bóng dài 0,6m. Tính chiều cao của cột điện.

Lời giải:

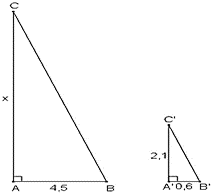
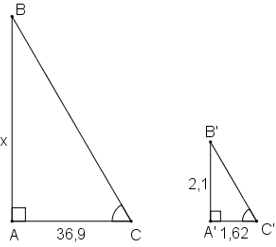
Gọi chiều cao cột điện là x (m); (x > 0).

Giả sử cột điện là AC, có bóng trên mặt đất là AB.

Thanh sắt là A'C', có bóng trên mặt đất là A'B'.

Vì cột điện và thanh sắt đều vuông góc với mặt đất nên hai tam giác ABC và A'B'C' đều là tam giác vuông.

Vì cùng một thời điểm tia sáng tạo với mặt đất một góc bằng nhau

Suy ra: $\widehat{B}=\widehat{B\text{'}}$

Xét tam giác ABC và tam giác A’B’C” có:

$$\begin{gathered} \widehat{B}=\widehat{B\text{'}} \\ \widehat{CAB}=\widehat{C\text{'}A\text{'}B\text{'}}=90° \end{gathered}$$

Suy ra: ∆ABC $~$ ∆A’B’C’(g – g)

Suy ra: $\frac{AC}{A\text{'}C\text{'}}=\frac{AB}{A\text{'}B\text{'}}$

Thay số: $\frac{x}{2,1}=\frac{4,5}{0,6}$

 $\Rightarrow x=\frac{2,1.4,5}{0,6}=15,75m$

Vậy cột điện cao 15,75m.

Bài 49 trang 84 Toán 8 Tập 2: Ở hình 51, tam giác ABC vuông ở A và có đường cao AH.

a) Trong hình vẽ có bao nhiêu cặp tam giác đồng dạng với nhau? (Hãy chỉ rõ từng cặp tam giác đồng dạng và viết theo các đỉnh tương ứng).

b) Cho biết AB = 12,45cm, AC = 20,50cm. Tính độ dài các đoạn thẳng BC, AH, BH và CH.

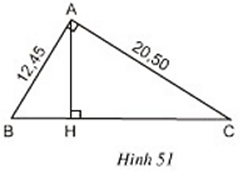
Lời giải:

a) Ta có:  ΔABC  $~$ ΔHBA   (1)

(vì $\widehat{BAC}=\widehat{AHB}$= 90º, $\widehat{B}$ chung  )

Và ΔABC  $~$ ΔHAC  (2)

(vì $\widehat{BAC}=\widehat{AHC}$ = 90º, $\widehat{C}$ chung)

Từ (1) và (2) suy ra: ΔHBA  $~$ ΔHAC vì cùng đồng dạng với ΔABC.

Vậy trong hình vẽ có ba cặp tam giác đồng dạng.

b)

Vì ΔABC vuông tại A, áp dụng định lý Pytago:

⇒ BC² = AB² + AC²

^{$$\begin{gathered} \Rightarrow BC=\sqrt{A{B}^2+\text{\hspace{0.17em}\hspace{0.17em}}A{C}^2} \\ =\sqrt{12,{45}^2+\text{\hspace{0.17em}}20,5^2}\approx 23,98\left(cm\right) \end{gathered}$$}

+ Vì ∆ABC $~$ ∆HBA ( chứng minh trên)  nên:

$\frac{AB}{HB}=\frac{BC}{AB}=\frac{AC}{AH}$ (tỉ lệ các cạnh tương ứng)

Ta có:

$$\begin{gathered} HB=\frac{A{B}^2}{BC}=\frac{12,{45}^2}{23,98}\approx 6,46cm \\ AH=\frac{AB.AC}{BC} \\ =\frac{12,45.20,5}{23,98}\approx 10,64cm \end{gathered}$$

Và HC = BC – HB $\approx 23,98-6,46=17,52cm$.

Bài 50 trang 84 Toán 8 Tập 2: Bóng của một ống khói nhà máy trên mặt đất có độ dài là 36,9m. Cùng thời điểm đó, một thanh sắt cao 2,1m cắm vuông góc với mặt đất có bóng dài 1,62m. Tính chiều cao của ống khói (h.52).

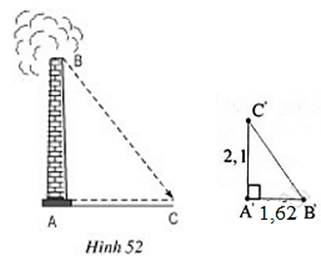
Lời giải:

Giả sử thanh sắt là A'B', có bóng là A'C'.

Vì ống khói và thanh sắt đều vuông góc với mặt đất nên hai tam giác ABC và A'B'C' đều là tam giác vuông.

Vì cùng một thời điểm nên tia sáng tạo với mặt đất các góc bằng nhau

$\Rightarrow \widehat{C}=\widehat{C\text{'}}$

Xét tam giác ABC và tam giác A’B’C’ có

$$\begin{gathered} \widehat{C}=\widehat{C\text{'}} \\ \widehat{CAB}=\widehat{C\text{'}A\text{'}B\text{'}}=90° \end{gathered}$$

Do đó: ∆ABC $~$  ∆A’B’C’ ( g.g).

$\Rightarrow \frac{AB}{A\text{'}B\text{'}}=\frac{AC}{A\text{'}C\text{'}}$

Thay số: $\frac{x}{2,1}=\frac{36,9}{1,62}$

 $\Rightarrow x=\frac{2,1.36,9}{1,62}\approx 47,83$

Vậy chiều cao ống khói là 47,83m.

Bài 51 trang 84 Toán 8 Tập 2: Chân đường cao AH của tam giác vuông ABC chia cạnh huyền BC thành hai đoạn thẳng có độ dài 25cm và 36cm. Tính chu vi và diện tích của tam giác vuông đó (h.53).

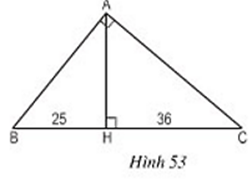
Lời giải:

+ BC = BH + HC = 25 + 36 = 61 (cm)

+ ΔABH vuông tại H và ΔABC vuông tại A có:

 $\widehat{B}$chung

$\widehat{AHB}=\widehat{BAC}={90}^0$

Do đó, ∆ABH  $~$ ∆CBA ( g.g)

$\Rightarrow \frac{BH}{AB}=\frac{AB}{BC}$.

⇒AB² = BH.BC = 25.(25 + 36) = 1525

$\Rightarrow AB=5\sqrt{61}\approx 39,05cm$

Áp dụng định lí Py – ta - go vào tam giác ABC vuông tại A có:

AB² + AC² = BC²

$$\begin{gathered} \Rightarrow AC=\sqrt{B{C}^2-A{B}^2} \\ =\sqrt{{61}^2-1525} \\ =6\sqrt{61}\approx 46,86cm \end{gathered}$$

Chu vi tam giác ABC là: 

P = AB + AC + BC  

$$\begin{gathered} =61+6\sqrt{61}+5\sqrt{61} \\ =61+\text{\hspace{0.17em}}11\sqrt{61} \left(cm\right) \end{gathered}$$ 

Diện tích tam giác ABC là

$$\begin{gathered} S=\frac{1}{2}AB.AC \\ =\frac{1}{2}.5\sqrt{61}.6\sqrt{61} \\ =915\left(c{m}^2\right) \end{gathered}$$

Bài 52 trang 85 Toán 8 Tập 2: Cho một tam giác vuông, trong đó cạnh huyền dài 20cm và một cạnh góc vuông dài 12cm. Tính độ dài hình chiếu cạnh góc vuông kia trên cạnh huyền.

Lời giải:

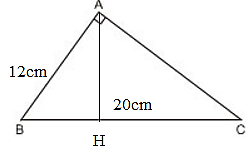
Giả sử ΔABC vuông tại A có đường cao AH, BC = 20cm, AB = 12cm. Ta tính HC.

Xét ΔABC và ΔHBA có:

$\widehat{BAC}=\widehat{BHA}={90}^0$

$\widehat{B}chung$

Do đó, ∆ABC $~$ ∆HBA  ( g.g)

Suy ra: $\frac{AB}{HB}=\frac{BC}{AB}$

$\Rightarrow HB=\frac{A{B}^2}{BC}=\frac{{12}^2}{20}=7,2cm$

Suy ra: HC = BC – HB = 20 - 7,2 = 12,8 cm.