Tailieumoi.vn xin giới thiệu Bài tập Toán 8 Chương 3 Bài 8: Các trường hợp đồng dạng của tam giác vuông. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 3 Bài 8: Các trường hợp đồng dạng của tam giác vuông. Mời các bạn đón xem:
Bài tập Toán 8 Chương 3 Bài 8: Các trường hợp đồng dạng của tam giác vuông
A. Bài tập Các trường hợp đồng dạng của tam giác vuông
I. Bài tập trắc nghiệm
Bài 1: Cho tam giác vuông ABC vuông tại A, chân đường cao AH của tam giác ABC chia cạnh huyền BC thành hai đoạn thẳng BH = 4cm, HC = 9cm. Tính diện tích tam giác ABC?
A. SABC = 39cm2
B. SABC = 36cm2
C. SABC = 78cm2
D. SABC = 18cm2
Áp dụng hệ thức lượng trong tam giác ABC vuông tại A
Ta có:
Vậy SABC = AB.AC = . = 39( cm2 )
Chọn đáp án A.
Bài 2: Cho Δ ABC và Δ MNP có , thì?
A. Δ ABC ∼ Δ PMN
B. Δ ABC ∼ Δ NMP
C. Δ ABC ∼ Δ MNP
D. Δ ABC ∼ Δ MPN
Ta có:
⇒ Δ ABC ∼ Δ MNP ( c - g - c )
Chọn đáp án C.
Bài 3: Nếu hai tam giác đồng dạng với nhau thì: Chọn phát biểu sai trong các phát biểu sau?
A. Tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng.
B. Tỉ số hai đường phân giác tương ứng bằng tỉ số đồng dạng.
C. Tỉ số hai đường trung tuyến tương ứng bằng tỉ số đồng dạng.
D. Tỉ số các chu vi bằng 2 lần tỉ số đồng dạng.
Áp dụng tính chất mở rộng
Nếu hai tam giác đồng dạng với nhau thì:
+ Tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng.
+ Tỉ số hai đường phân giác tương ứng bằng tỉ số đồng dạng.
+ Tỉ số hai đường trung tuyến tương ứng bằng tỉ số đồng dạng.
+ Tỉ số các chu vi bằng tỉ số đồng dạng.
Đáp án D sai.
Chọn đáp án D.
Bài 4: Cho hai tam giác ABC và DEF có ,AB = 3cm, BC = 5cm, EF = 10cm, DF = 6cm. Chọn phát biểu đúng trong các phát biểu sau?
A. Δ ABC ∼ Δ DEF
B. Δ ABC ∼ Δ EDF
C. Δ ABC ∼ Δ DFE
D. Δ ABC ∼ Δ FDE
Ta có:
⇒ Δ ABC ∼ Δ DFE ( c - g - c )
Chọn đáp án C.
Bài 5: Cho tam giác ABC có AB = 3cm; AC = 4cm và BC = 5cm. Tam giác MNP vuông tại M có MN = 6cm; MP = 8cm. Tìm khẳng định sai
A. Tam giác ABC là tam giác vuông
B. Δ ABC và ΔMNP đồng dạng với nhau
C. NP = 10 cm
D. Có hai phương án sai
Ta có: AB2 + AC2 = BC2 ( 32 + 42 = 52 = 25)
Suy ra: tam giác ABC vuông tại A
Xét Δ ABC và Δ MNP có:
Suy ra: Δ ABC và ΔMNP đồng dạng với nhau.
Áp dụng định lí Pyta go vào tam giác MNP có:
NP2 = MN2 + MP2 = 62 + 82 = 100 nên NP = 10cm
Chọn đáp án D
Bài 6: Cho tam giác ABC vuông tại A, kẻ AH vuông góc BC. Tìm tam giác đồng dạng với tam giác ABC?
A. ΔHAC
B. ΔAHC
C. ΔAHB
D. ΔABH
Xét ΔABC và ΔHAC có:
Suy ra: ΔABC đồng dạng với ΔHAC ( g.g)
Chọn đáp án A
Bài 7: Cho ta giác ABC vuông tại A, kẻ AH vuông góc BC. Biết BH = 25 và HC = 36. Tính AH?
A. 18cm
B. 25cm
C. 20cm
D. 32cm
Xét ΔAHB và ΔCHA có:
Suy ra: ΔAHB và ΔCHA đồng dạng với nhau ( g.g)
Chọn đáp án C
Bài 8: Cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC. Biết BC = 20cm, AC = 12cm. Tính BH?
A. 12cm
B. 12,5cm
C. 15cm
D. 12,8cm
Áp dụng định lí Pytago vào tam giác ABC ta có:
BC2 = AB2 + AC2 suy ra: AB2 = BC2 - AC2 = 202 - 122 = 256
Nên AB = 16cm
* Xét tam giác AHB và tam giác CAB có:
Suy ra: Δ AHB và CAB đồng dạng ( g.g) .
Chọn đáp án D
Bài 9: Cho tam giác ABC vuông tại A, kẻ đường cao AH. Biết AH = 6cm, BH = 3cm. Tính AC?
Chọn đáp án C
Bài 10: Cho tam giác ABC có AB = 3cm, AC = 4cm, BC = 5cm . Tam giác MNP đồng dạng với tam giác ABC và diện tích tam giác MNP là 96 cm2. Tính độ dài các cạnh của tam giác MNP?
A. 9cm, 12cm, 15cm
B. 12cm, 16cm ; 20cm
C. 6cm, 8cm, 10cm
D. Đáp án khác
Ta có: AB2 + AC2 = BC2 (32 + 42 = 52
Suy ra: tam giác ABC vuông tại A.
Diện tích tam giác ABC là:
*Gọi tam giác ABC đồng dạng với tam giác MNP theo tỉ số k
Suy ra:
Thay số
Chọn đáp án B
II. Bài tập tự luận có lời giải
Bài 1: Cho tam giác ABC cân tại A, AC = 20cm, BC = 24cm, các đường cao AD và CE cắt nhau ở H. Tính độ dài HD.
Lời giải
Tam giác ABC cân tại A nên BD = DC = 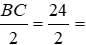
Theo định lý Py-ta-go, ta có AD2 = AC2 - DC2 = 202 - 122 = 162
Nên AD = 16cm
Xét ΔCDH và ΔADB có:
(cùng phụ với B)
Do đó ΔCDH ~ ΔADB (g.g)
Nên
Suy ra HD = 9cm.
Bài 2 Cho tam giác ABC cân tại A, AC = 20cm, BC = 24cm, các đường cao AD và CE cắt nhau ở H. Độ dài AH là?
Lời giải
Tam giác ABC cân tại A nên BD = DC = 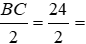
Theo định lý Py-ta-go, ta có AD2 = AC2 - DC2 = 202 - 122 = 162
Nên AD = 16cm
Xét ΔCDH và ΔADB có:
(cùng phụ với B)
Do đó ΔCDH ~ ΔADB (g.g)
Nên
Suy ra HD = 9cm ⇒ AH = AD - HD = 16 - 9 = 7cm
Bài 3 Với giả thiết được cho trong hình, kết quả nào sau đây là đúng?
Lời giải
Xét 2 tam giác vuông ΔADO() và ΔECO () ta có:
(2 góc đối đỉnh)
⇒ ΔADO ~ ΔECO (g.g)
Vì ΔADO vuông tại A nên áp dụng định lý Pitago ta có:
AD2 + AO2 = OD2 ⇔ 42 + AO2 = 52 ⇔ AO2 = 52 - 42 = 9 ⇒ AO = 3
Xét 2 tam giác vuông ΔCEO () và ΔCAB () có: C chung
Vậy x = 4,8; y = 6,45.
Bài 4 Với giả thiết được cho trong hình, kết quả nào sau đây là đúng?
Lời giải
Xét 2 tam giác vuông ΔADO() và ΔECO () ta có:
(2 góc đối đỉnh)
⇒ ΔADO ~ ΔECO (g.g)
Vì ΔADO vuông tại A nên áp dụng định lý Pitago ta có:
AD2 + AO2 = OD2 ⇔ 42 + AO2 = 52 ⇔ AO2 = 52 - 42 = 9 ⇒ AO = 3
Xét 2 tam giác vuông ΔCEO () và ΔCAB () có: C chung
Vậy x = 4,8; y = 6,45.
Bài 5 Cho tam giác ABC vuông ở A, đường cao AH. Tính HB.HC bằng?
Lời giải
Ta có:
Mà: (2 góc phụ nhau)
⇒
Xét 2 tam giác vuông AHB và CHA ta có: (cmt)
⇒ ΔAHB ~ ΔCHA (g - g)
⇒ 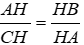
Bài 6 Hãy chỉ ra các cặp tam giác đồng dạng trong hình 47.
Lời giải
Hai tam giác vuông ΔDEF và ΔD’E’F’ có
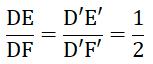
⇒ ΔABD ∼ ΔACB (hai cạnh góc vuông)
Áp dụng định lí Py – ta – go:
A'C'2 = B'C'2 - A'B'2 = 52 -22 = 21 ⇒ A'C' =
AC2 = BC2 - AB2 = 102 - 42 = 84 ⇒ AC =
Hai tam giác vuông ΔABC và ΔA’B’C’ có
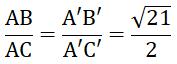
⇒ ΔABC ∼ ΔA’B’C’ (hai cạnh góc vuông)
Lời giải:
Bài 8 Tam giác ABC có độ dài các cạnh là 3cm, 4cm, 5cm. Tam giác A'B'C' đồng dạng với tam giác ABC và có diện tích là 54cm2. Tính độ dài các cạnh của tam giác A'B'C'.
Lời giải:
Xét ΔABC có: AB2 + AC2 = 32 + 42 = 25 = 52 = BC2
⇒ ΔABC vuông tại A (Định lý Pytago đảo)
⇒ Diện tích tam giác ABC bằng:
(với k là tỉ số đồng dạng).
Lại có tỉ số diện tích bằng bình phương tỉ số đồng dạng
⇒ A’B’ = 3.AB = 3.3 = 9 (cm)
B’C’ = 3.BC = 3.5 = 15 (cm)
C’A’ = 3.CA = 3.4 = 12 (cm)
Vậy độ dài ba cạnh của tam giác lần lượt là 9cm, 12cm, 15cm.
Bài 9 Bóng của cột điện trên mặt đất có độ dài là 4,5m. Cùng thời điểm đó, một thanh sắt cao 2,1m cắm vuông góc với mặt đất có bóng dài 0,6m. Tính chiều cao của cột điện.
Lời giải:
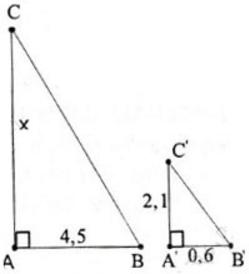
Giả sử cột điện là AC, có bóng trên mặt đất là AB.
Thanh sắt là A'C', có bóng trên mặt đất là A'B'.
Vì cột điện và thanh sắt đều vuông góc với mặt đất nên hai tam giác ABC và A'B'C' đều là tam giác vuông.
Vì cùng một thời điểmc tia sáng chiếu nên ta suy ra
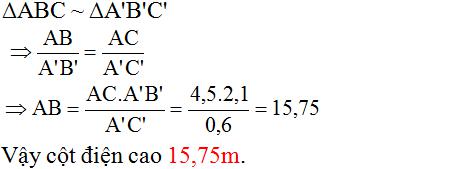
Bài 10 Ở hình 51, tam giác ABC vuông ở A và có đường cao AH.
a) Trong hình vẽ có bao nhiêu cặp tam giác đồng dạng với nhau? (Hãy chỉ rõ từng cặp tam giác đồng dạng và viết theo các đỉnh tương ứng).
b) Cho biết AB = 12,45cm, AC = 20,50cm. Tính độ dài các đoạn thẳng BC, AH, BH và CH.
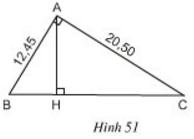
Lời giải:

III. Bài tập vận dụng
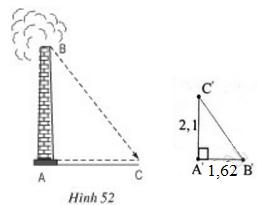
Bài 1 Bóng của một ống khói nhà máy trên mặt đất có độ dài là 36,9m. Cùng thời điểm đó, một thanh sắt cao 2,1m cắm vuông góc với mặt đất có bóng dài 1,62m. Tính chiều cao của ống khói (h.52).
Bài 2 Chân đường cao AH của tam giác vuông ABC chia cạnh huyền BC thành hai đoạn thẳng có độ dài 25cm và 36cm. Tính chu vi và diện tích của tam giác vuông đó (h.53).
Bài 3 Cho một tam giác vuông, trong đó cạnh huyền dài 20cm và một cạnh góc vuông dài 12cm. Tính độ dài hình chiếu cạnh góc vuông kia trên cạnh huyền.
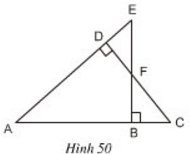
Bài 4 Trên hình 50 hãy chỉ ra các tam giác đồng dạng. Viết các tam giác này theo thứ tự các đỉnh tương ứng và giải thích vì sao chúng đồng dạng?

Bài 5 Tam giác ABC có độ dài các cạnh là 3cm, 4cm, 5cm. Tam giác A'B'C' đồng dạng với tam giác ABC và có diện tích là 54 . Tính độ dài cách cạnh của tam giác A'B'C'.
Bài 6 Bóng của một cột điện trên mặt đất có độ dài là 4,5m. Cùng thời điểm đó, một thanh sắt cao 2,1m cắm vuông góc với mặt đất có bóng dài 0,6m. Tính chiều cao của cột điện.
Bài 7 Ở hình 51, tam giác ABC vuông ở A và có đường cao AH.
a) Trong hình vẽ có bao nhiêu cặp tam giác đồng dạng với nhau? (Hãy chỉ rõ từng cặp tam giác đồng dạng và viết theo các đỉnh tương ứng).
b) Cho biết AB = 12,45cm, AC = 20,50cm. Tính độ dài các đoạn thẳng BC, AH, BH và CH.

Bài 8 Bóng của một ống khói nhà máy trên mặt đất có độ dài là 36,9m. Cùng thời điểm đó, một thanh sắt cao 2,1m cắm vuông góc với mặt đất có bóng dài 1,62m. Tính chiều cao của ống khói (h.52).

Bài 9 Chân đường cao AH của tam giác vuông ABC chia cạnh huyền BC thành hai đoạn thẳng có độ dài 25cm và 36cm. Tính chu vi và diện tích của tam giác vuông đó (h.53).
Hướng dẫn: Trước tiên tìm cách tính AH từ các tam giác vuông đồng dạng, sau đó tính các cạnh của tam giác ABC.

Bài 10 Cho một tam giác vuông, trong đó cạnh huyền dài 20cm và một cạnh góc vuông dài 12cm. Tính độ dài hình chiếu cạnh góc vuông kia trên cạnh huyền.
B. Lý thuyết Các trường hợp đồng dạng của tam giác vuông
1. Áp dụng các trường hợp đồng dạng của tam giác vào tam giác vuông
Hai tam giác vuông đồng dạng với nhau nếu:
+ Tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia.
+ Tam giác vuông này có hai cạnh góc vuông tỉ lệ với hai cạnh góc vuông của tam giác vuông kia.
2. Dấu hiệu đặc biệt nhận biết hai tam vuông đồng dạng
Định lý 1: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
Tổng quát: Δ ABC,Δ A'B'C', Aˆ = A'ˆ = 900; B'C'/BC = A'B'/AB
\Rightarrow Δ ABC ∈ Δ A'B'C'.
3. Tỉ số hai đường cao, tỉ số diện tích của hai tam giác đồng dạng
Định lý 2: Tỉ số hai đường cao tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.
Tổng quát: Ta có tỉ số đồng dạng là
Tỉ số hai đường cao là :
Định lý 3: Tỉ số diện tích hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng.
Tổng quát: Ta có tỉ số đồng dạng là
Tỉ số diện tích hai tam giác đồng dạng là :
4. Mở rộng
Nếu hai tam giác đồng dạng với nhau thì:
+ Tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng.
+ Tỉ số hai đường phân giác tương ứng bằng tỉ số đồng dạng.
+ Tỉ số hai đường trung tuyến tương ứng bằng tỉ số đồng dạng.
+ Tỉ số các chu vi bằng tỉ số đồng dạng.
+ Tỉ số các diện tích bằng bình phương tỉ số đồng dạng.
5. Ví dụ áp dụng
Ví dụ: Cho tam giác đồng dạng với tam giác ABC theo tỉ số k = 4/3. Tính chu vi của tam giác ABC, biết chu vi của tam giác A'B'C' bằng 27cm.
Hướng dẫn:
Ta có Δ A'B'C' ∈ Δ ABC theo tỉ số k
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:





