Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh bộ câu hỏi trắc nghiệm Toán lớp 8: Các trường hợp đồng dạng của tam giác vuông có đáp án chi tiết, chọn lọc. Tài liệu gồm 22 câu hỏi trắc nghiệm cực hay bám sát chương trình sgk Toán 8. Hi vọng với bộ câu hỏi trắc nghiệm Các trường hợp đồng dạng của tam giác vuông có đáp án này sẽ giúp bạn ôn luyện kiến thức để đạt kết quả cao trong bài thi môn Toán 8 sắp tới.
Giới thiệu về tài liệu:
- Số câu hỏi trắc nghiệm: 22 câu
- Lời giải & đáp án: có
Mời quí bạn đọc tải xuống để xem đầy đủ tài liệu Trắc nghiệm Các trường hợp đồng dạng của tam giác vuông có đáp án – Toán lớp 8:

Bài 8: Các trường hợp đồng dạng của tam giác vuông
Bài 1: Cho ΔDHE ~ ΔABC với tỉ số đồng dạng 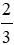
(I) Tỉ số hai đường cao tương ứng của ΔDHE và ΔABC là 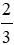
(II) Tỉ số hai đường cao tương ứng của ΔABC và ΔDHE là 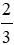
(III) Tỉ số diện tích của ΔABC và ΔDHE là 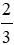
(IV) Tỉ số diện tích của ΔDHE và ΔABC là 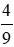
A. 2
B. B. 1
C. C. 3
D. D. 4
Lời giải
Vì ΔDHE ~ ΔABC với tỉ số đồng dạng 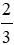
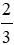
Do đó (I) và (IV) đúng, (II) và (III) sai.
Đáp án cần chọn là: A
Bài 2: Cho ΔABC ~ ΔDHE với tỉ số đồng dạng 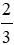
Lời giải
Vì ΔABC ~ ΔDHE với tỉ số đồng dạng 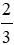

Vậy tỉ số hai đường cao tương ứng của ΔDHE và ΔABC là
Đáp án cần chọn là: B
Bài 3: Cho tam giác ABC cân tại A, đường cao CE. Tính AB, biết BC = 24cm và BE = 9cm.
A. 16cm
B. 32cm
C. 24cm
D. 18cm
Lời giải
Kẻ đường cao AD. Xét ΔCBE và ΔABD có 
Đáp án cần chọn là: B
Bài 4: Cho tam giác ABC cân tại A. Đường thẳng qua C và vuông góc AB tại CE. Tính AB, biết BC = 18cm và BE = 6,75cm.
A. 16cm
B. 32cm
C. 24cm
D. 18cm
Lời giải
Kẻ đường cao AD. Xét ΔCBE và ΔABD có góc BEC = góc ADB = 900 và góc B chung nên ΔCBE ~ ΔABD (g.g)
Đáp án cần chọn là: C
Bài 5: Tam giác ABC vuông tại A có đường cao AH. Cho biết AB = 3cm; AC = 4cm. Tính độ dài các đoạn thẳng HA, HB.
A. HA = 2,4cm; HB = 1,2cm
B. B. HA = 2cm; HB = 1,8cm
C. HA = 2cm; HB = 1,2cm
D. D. HA = 2,4cm; HB = 1,8cm
Lời giải
Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
AB2 + AC2 = BC2 ⇔ 32 + 42 = BC2 ⇔ BC2 = 25 ⇒ BC = 25cm
Xét 2 tam giác vuông ABC và HBA có: B chung
Nên HA = 2,4cm; HB = 1,8cm.
Đáp án cần chọn là: D
Bài 6: Cho ΔABC ~ ΔDHE với tỉ số đồng dạng 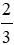
Lời giải
Vì ΔABC ~ ΔDHE với tỉ số đồng dạng 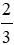

Vậy tỉ số hai đường cao tương ứng của ΔDHE và ΔABC là
Đáp án cần chọn là: B
Bài 7: Cho tam giác ABC cân tại A, đường cao CE. Tính AB, biết BC = 24cm và BE = 9cm.
A. 16cm
B. 32cm
C. 24cm
D. 18cm
Lời giải
Kẻ đường cao AD. Xét ΔCBE và ΔABD có 
Đáp án cần chọn là: B
Bài 8: Cho tam giác ABC cân tại A. Đường thẳng qua C và vuông góc AB tại CE. Tính AB, biết BC = 18cm và BE = 6,75cm.
A. 16cm
B. 32cm
C. 24cm
D. 18cm
Lời giải
Kẻ đường cao AD. Xét ΔCBE và ΔABD có góc BEC = góc ADB = 900 và góc B chung nên ΔCBE ~ ΔABD (g.g)
Đáp án cần chọn là: C
Bài 9: Tam giác ABC vuông tại A có đường cao AH. Cho biết AB = 3cm; AC = 4cm. Tính độ dài các đoạn thẳng HA, HB.
A. HA = 2,4cm; HB = 1,2cm
B. B. HA = 2cm; HB = 1,8cm
C. HA = 2cm; HB = 1,2cm
D. D. HA = 2,4cm; HB = 1,8cm
Lời giải
Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
AB2 + AC2 = BC2 ⇔ 32 + 42 = BC2 ⇔ BC2 = 25 ⇒ BC = 25cm
Xét 2 tam giác vuông ABC và HBA có: B chung
Nên HA = 2,4cm; HB = 1,8cm.
Đáp án cần chọn là: D
Bài 10: Tam giác ABC vuông tại A có đường cao AH. Cho biết AB = 3cm; AC = 4cm. Chọn kết luận không đúng.
A. HA = 2,4cm
B. B. HB = 1,8cm
C. C. HC = 3,2cm
D. D. BC = 6cm
Lời giải
Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
AB2 + AC2 = BC2 ⇔ 32 + 42 = BC2 ⇔ BC2 = 25 ⇒ BC = 25cm
Xét 2 tam giác vuông ABC và HBA có: B chung
Nên HA = 2,4cm; HB = 1,8cm; HC = 3,2cml BC = 5cm
Đáp án cần chọn là: D
Bài 11: Cho tam giác ABC cân tại A, AC = 20cm, BC = 24cm, các đường cao AD và CE cắt nhau ở H. Tính độ dài HD.
A. 12cm
B. 6cm
C. 9cm
D. 10cm
Lời giải
Tam giác ABC cân tại A nên BD = DC = 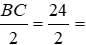
Theo định lý Py-ta-go, ta có AD2 = AC2 - DC2 = 202 - 122 = 162
Nên AD = 16cm
Xét ΔCDH và ΔADB có:
góc CDH = góc ADB = 900
góc C1 = góc A1 (cùng phụ với B)
Do đó ΔCDH ~ ΔADB (g.g)
Nên
Suy ra HD = 9cm.
Đáp án cần chọn là: C
Bài 12: Cho tam giác ABC cân tại A, AC = 20cm, BC = 24cm, các đường cao AD và CE cắt nhau ở H. Độ dài AH là:
A. 12cm
B. 7cm
C. 9cm
D. 10cm
Lời giải
Tam giác ABC cân tại A nên BD = DC = 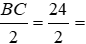
Theo định lý Py-ta-go, ta có AD2 = AC2 - DC2 = 202 - 122 = 162
Nên AD = 16cm
Xét ΔCDH và ΔADB có:
góc CDH = góc ADB = 900
góc C1 = góc A1 (cùng phụ với B)
Do đó ΔCDH ~ ΔADB (g.g)
Nên
Suy ra HD = 9cm ⇒ AH = AD - HD = 16 - 9 = 7cm
Đáp án cần chọn là: B
Bài 13: Với giả thiết được cho trong hình, kết quả nào sau đây là đúng?
A. y = 10
B. x = 4,8
C. x = 5
D. y = 8,25
Lời giải
Xét 2 tam giác vuông ΔADO(DAO = 900) và ΔECO (CEO = 900) ta có:
góc AOD = góc EOC (2 góc đối đỉnh)
⇒ ΔADO ~ ΔECO (g.g)
Vì ΔADO vuông tại A nên áp dụng định lý Pitago ta có:
AD2 + AO2 = OD2 ⇔ 42 + AO2 = 52 ⇔ AO2 = 52 - 42 = 9 ⇒ AO = 3
Xét 2 tam giác vuông ΔCEO (CEO = 900) và ΔCAB (CAB = 900) có: C chung
Vậy x = 4,8; y = 6,45.
Đáp án cần chọn là: B
Bài 14: Với giả thiết được cho trong hình, kết quả nào sau đây là đúng?
A. y = 10
B. x = 3,2
C. y = 5
D. y = 6,45
Lời giải
Xét 2 tam giác vuông ΔADO(DAO = 900) và ΔECO (CEO = 900) ta có:
góc AOD = góc EOC (2 góc đối đỉnh)
⇒ ΔADO ~ ΔECO (g.g)
Vì ΔADO vuông tại A nên áp dụng định lý Pitago ta có:
AD2 + AO2 = OD2 ⇔ 42 + AO2 = 52 ⇔ AO2 = 52 - 42 = 9 ⇒ AO = 3
Xét 2 tam giác vuông ΔCEO (CEO = 900) và ΔCAB (CAB = 900) có: C chung
Vậy x = 4,8; y = 6,45.
Đáp án cần chọn là: D
Bài 15: Cho tam giác ABC vuông ở A, đường cao AH.
1. Tính HB.HC bằng
A. AB2
B. B. AH2
C. C. AC2
D. D. BC2
Lời giải
Ta có: HAB + HAC = BAC = 900
Mà: HBA + HAB = 900 (2 góc phụ nhau)
⇒ góc HAC = góc HBA
Xét 2 tam giác vuông AHB và CHA ta có: góc HAC = góc HBA (cmt)
⇒ ΔAHB ~ ΔCHA (g - g)
⇒ 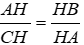
Đáp án cần chọn là: B
2. Cho BH = 9cm, HC = 16cm. Tính diện tích của tam giác ABC.
A. 250cm2
B. B. 300cm2
C. C. 150cm2
D. D. 200cm2
Lời giải
Với BH = 9cm, HC = 16cm ⇒ BC = BH + HC = 9 + 16 = 25 cm
Ta có: AH2 = HB.HC (cmt)
⇒ AH2 = 9.16 = 144 ⇒ AH = 12cm
Nên diện tích tam giác ABC là SABC = 

Đáp án cần chọn là: C
Bài 16: Cho tam giác ABC vuông ở A, đường cao AH = 16cm, BH = 8cm.
1. Tính HB.HC bằng:
A. 16
B. 256
C. 4
D. 32
Lời giải
Ta có: HAB + HAC = BAC = 900
Mà: HBA + HAB = 900 (2 góc phụ nhau)
⇒ góc HAC = góc HBA
Xét 2 tam giác vuông AHB và CHA ta có: góc HAC = góc HBA (cmt)
⇒ ΔAHB ~ ΔCHA (g - g)
⇒ 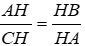
Đáp án cần chọn là: B
2. Tính diện tích tam giác ABC.
A. 320cm2
B. 300cm2
C. 150cm2
D. 200cm2
Lời giải
Ta có: AH2 = HB.HC (cmt)
⇒ 162 = 8.HC ⇒ HC = 32cm
⇒ BC = BH + HC = 8 + 32 = 40 cm
Nên diện tích tam giác ABC là SABC = 

Đáp án cần chọn là: A
Bài 17: Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm, đường cao AH, đường phân giác BD.
1. Tính độ dài các đoạn AD, DC lần lượt là
A. 6cm, 4cm
B. 2cm, 5cm
C. 5cm, 3cm
D. 3cm, 5cm
Lời giải
+ Áp dụng định lý Pitago trong tam giác vuông ABC ta có:
AB2 + AC2 = BC2 ⇔ 62 + 82 = BC2 ⇔ BC2 = 100 ⇒ BC = 10cm
+ Vì BD là đường phân giác của tam giác ABC nên áp dụng tính chất đường phân giác của tam giác, ta có:
⇒ AD = 3cm ⇒ DC = AC - AD = 8 - 3 = 5cm
Đáp án cần chọn là D.
2. Gọi I là giao điểm của AH và BD. Chọn câu đúng.
A. AB.BI = BD.HB
B. AB.BI = AI2
C. AB.BI = BD2
D. AB.BI = HI2
Lời giải
Xét 2 tam giác vuông ABD và HBI có:
góc ABD = góc HBI (BD là tia phân giác của góc B)
⇒ ΔABD ~ ΔHBI (g - g)
⇒ 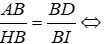
Đáp án cần chọn là: A
Bài 18: Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm, đường cao AH, đường phân giác BD. Gọi I là giao điểm của AH và BD.
1. Chọn kết luận đúng.
A. AD = 6cm
B. DC = 5cm
C. AD = 5cm
D. BC = 12cm
Lời giải
+ Áp dụng định lý Pitago trong tam giác vuông ABC ta có:
AB2 + AC2 = BC2 ⇔ 62 + 82 = BC2 ⇔ BC2 = 100 ⇒ BC = 10cm
+ Vì BD là đường phân giác của tam giác ABC nên áp dụng tính chất đường phân giác của tam giác, ta có:
⇒ AD = 3cm ⇒ DC = AC - AD = 8 - 3 = 5cm
Đáp án cần chọn là: B
2. Chọn khẳng định đúng.
A. AB.BI = BD.HB
B. AB.BI = AI2
C. AB.BI = BD2
D. AB.BI = HI2
Lời giải
Xét 2 tam giác vuông ABD và HBI có:
góc ABD = góc HBI (BD là tia phân giác của góc B)
⇒ ΔABD ~ ΔHBI (g - g)
⇒ 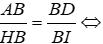
Đáp án cần chọn là: A
Bài 19: Cho tam giác ABC, phân giác AD. Gọi E, F lần lượt là hình chiếu của B và C lên AD. Chọn khẳng định đúng.
A. AE.DF = AD2
B. AE.DF = ED2
C. AE.DF = AF.DE
D. AE.DF = BD2
Lời giải
Xét 2 tam giác vuông ABE và ACF ta có:
góc BAE = góc CAF (vì AD là tia phân giác của góc A)
⇒ ΔABE ~ ΔACF (g - g)
Xét 2 tam giác vuông BDE và CDF ta có:
góc EDB = góc FDC (2 góc đối đỉnh)
⇒ ΔBDE ~ ΔCDF (g - g)
Từ (1) và (2) ta có: 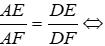
Đáp án cần chọn là: C
Bài 20: Cho tam giác ABC, phân giác AD. Gọi E, F lần lượt là hình chiếu của B và C lên AD. Chọn khẳng định không đúng.
A. AE.CF = AF.BE
B. AE.DF = ED2
C. AE.DF = AF.DE
D. 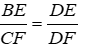
Lời giải
Xét 2 tam giác vuông ABE và ACF ta có:
góc BAE = góc CAF (vì AD là tia phân giác của góc A)
⇒ ΔABE ~ ΔACF (g - g)
⇒ AE.CF = AF.BE hay A đúng
Xét 2 tam giác vuông BDE và CDF ta có:
góc EDB = góc FDC (2 góc đối đỉnh)
⇒ ΔBDE ~ ΔCDF (g - g)
Từ (1) và (2) ta có: 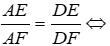
Đáp án cần chọn là: B
Bài 21: Cho tam giác ABC vuông tại A, đường cao AH chia cạnh BC thành hai đoạn thẳng HB = 7cm và HC = 18cm. Điểm E thuộc đoạn thẳng HC sao cho đường thẳng đi qua E và vuông góc với BC chia tam giác ABC thành hai phần có diện tích bằng nhau. Tính CE.
A. 15cm
B. 12cm
C. 10cm
D. 8cm
Lời giải
Gọi D là giao điểm của AC và đường vuông góc với BC tại E.
Xét ΔAHC và ΔABC có C chung và góc AHC = góc BAC = 900 nên ΔAHC ~ ΔBAC (g-g)
Vì DE // AH (cùng vuông với BC) duy ra ΔDEC ~ ΔAHC nên
Từ (3) và (4) suy ra 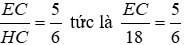
Đáp án cần chọn là: A
Bài 22: Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 3,5cm và HC = 9cm. Điểm E thuộc đoạn thẳng HC sao cho đường thẳng đi qua E và vuông góc với BC chia tam giác ABC thành hai phần có diện tích bằng nhau. Tính CE.
A. 10cm
B. B. 6cm
C. C. 5cm
D. D. 7,5cm
Lời giải
Gọi D là giao điểm của AC và đường vuông góc với BC tại E.
Xét ΔAHC và ΔABC có C chung và góc AHC = góc BAC = 900 nên ΔAHC ~ ΔBAC (g-g)
Vì DE // AH (cùng vuông với BC) duy ra ΔDEC ~ ΔAHC nên
Từ (3) và (4) suy ra 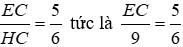
Đáp án cần chọn là: D
Bài giảng Toán 8 Bài 8: Các trường hợp đồng dạng của tam giác vuông