Với lời giải SBT Toán 7 trang 83 Tập 1 chi tiết trong Bài 3: Hai đường thẳng song song sách Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài 3:Hai đường thẳng song song

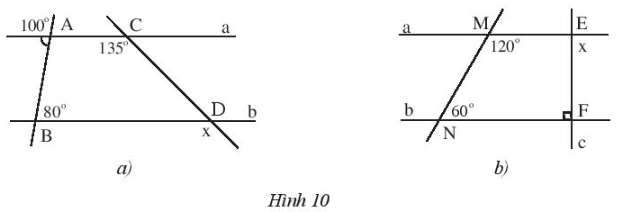
Bài 1 trang 83 Sách bài tập Toán 7 Tập 1: Cho biết a // b, tìm các số đo x trong Hình 10.

Lời giải

a) Vì a // b nên AC // BD.

Suy ra $x=\widehat{ACD}=135°$ (hai góc đồng vị).

b) Vì a // b nên ME // NF.

Suy ra $x=\widehat{NFE}=90°$ (hai góc so le trong).

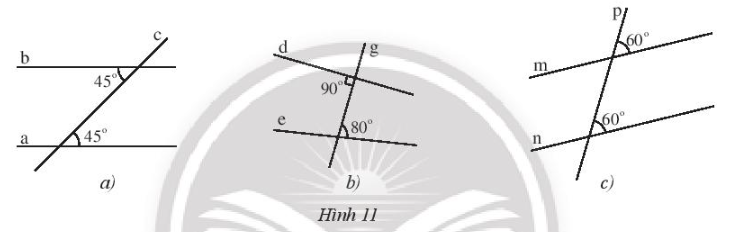
Bài 2 trang 83 Sách bài tập Toán 7 Tập 1: Tìm các cặp đường thẳng song song trong Hình 11 và giải thích.

Lời giải

a)

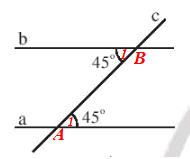
Đặt các góc A₁ và B₁ như hình vẽ trên.

Ta có ${\widehat{A}}_1={\widehat{B}}_1=45°$

Mà ${\widehat{A}}_1$ và ${\widehat{B}}_1$ là hai góc so le trong.

Do đó a // b.

Vậy trong Hình 11a có a // b.

b)

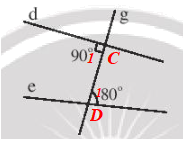
Đặt các góc C₁ và D₁ như hình vẽ trên.

Ta có ${\widehat{C}}_1$ và ${\widehat{D}}_1$ ở vị trí so le trong nhưng hai góc này không có số đo bằng nhau $\left({\widehat{C}}_1=90°\ne {\widehat{D}}_1=80°\right)$ nên hai đường thẳng d và e không song song với nhau.

Vậy trong Hình 11b không có hai đường thẳng nào song song.

c)

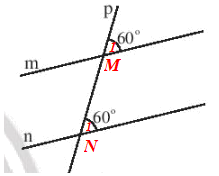
Đặt các góc M₁ và N₁ như hình vẽ trên.

Ta có ${\widehat{M}}_1={\widehat{N}}_1=60°$

Mà ${\widehat{M}}_1$ và ${\widehat{N}}_1$ là hai góc đồng vị.

Do đó m // n.

Vậy trong Hình 11c có m // n.

Bài 3 trang 83 Sách bài tập Toán 7 Tập 1:

a) Cho tam giác ABC. Hãy nêu cách vẽ đường thẳng a đi qua đỉnh A và song song với BC, cách vẽ đường thẳng b đi qua B và song song với AC.

b) Có thể vẽ được bao nhiêu đường thẳng a, bao nhiêu đường thẳng b? Vì sao?

Lời giải

a) • Ta vẽ đường thẳng xy đi qua A sao cho $\widehat{xAB}=\widehat{ABC}.$

Vì $\widehat{xAB}=\widehat{ABC}.$ mà hai góc này ở vị trí so le trong

Nên xy // BC.

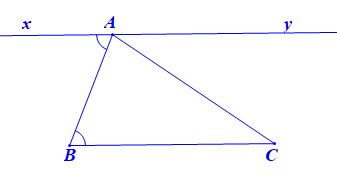
Vậy đường thẳng xy là đường thẳng cần vẽ đi qua A và song song với BC.

• Ta vẽ đường thẳng zt đi qua B sao cho $\widehat{tBC}=\widehat{BCA}.$

Vì $\widehat{tBC}=\widehat{BCA}.$ mà hai góc này ở vị trí so le trong

Nên zt // AC.

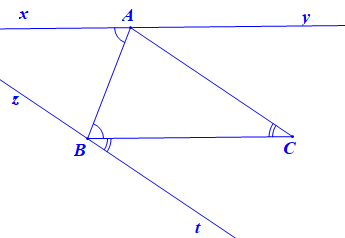
Vậy đường thẳng zt là đường thẳng cần vẽ đi qua B và song song với AC.

b) Theo tiên đề Euclid ta có qua một điểm nằm ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.

Vậy ta chỉ vẽ được một đường thẳng a và một đường thẳng b.

Bài 4 trang 83 Sách bài tập Toán 7 Tập 1: Tìm các góc có số đo bằng nhau của hai tam giác ABC và DEC trong Hình 12.

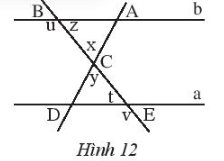
Lời giải

Bài 5 trang 83 Sách bài tập Toán 7 Tập 1: Cho Hình 13.

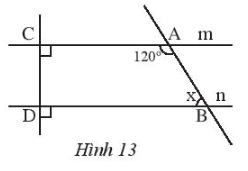
a) Vì sao m // n?

b) Tính số đo x của góc ABD.

Lời giải   

a) Vì m ⊥ CD và n ⊥ CD

Nên m // n (cùng vuông góc với CD).

Vậy m // n.

b) Đặt góc B₁ như hình vẽ dưới đây:

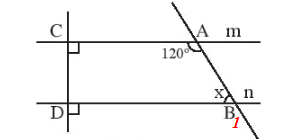
Vì m // n (theo câu a) nên:

${\widehat{B}}_1=\widehat{CAB}=120°$ (hai góc đồng vị)

Lại có $\widehat{ABD}$ và ${\widehat{B}}_1$ là hai góc kề bù nên:

$\widehat{ABD}+{\widehat{B}}_1=180°$

Suy ra $\widehat{ABD}=180°-{\widehat{B}}_1=180°-120°=60°$

Hay x = 60°.

Vậy x = 60°.

Xem thêm các bài giải sách bài tập Toán 7 Chân trời sáng tạo hay, chi tiết khác:

Giải SBT Toán 7 trang 84 Tập 1