Với lời giải SBT Toán 7 trang 36 Tập 2 chi tiết trong Bài tập cuối chương 7 sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài tập cuối chương 7

Bài 7.35 trang 36 SBT Toán 7 Tập 2: Cho hai đa thức f(x) = 4x⁴ − 5x³ + 3x + 2 và g(x) = −4x⁴ + 5x³ + 7. Trong các số −4; −3; 0 và 1, số nào là nghiệm của đa thức f(x) + g(x)?

Lời giải:

Ta có: f(x) + g(x)

= (4x⁴ − 5x³ + 3x + 2) + (−4x⁴ + 5x³ + 7)

= 4x⁴ − 5x³ + 3x + 2 −4x⁴ + 5x³ + 7

= (4x⁴ −4x⁴) + (−5x³ + 5x³) + 3x + (2 + 7)

= 3x + 9.

Để tìm nghiệm của đa thức f(x) + g(x) thì đa thức phải bằng 0.

Suy ra 3x + 9 = 0

x = (−9) : 3 = −3

Vậy nghiệm của đa thức f(x) + g(x) là x = −3

Bài 7.36 trang 36 SBT Toán 7 Tập 2: Cho hai đa thức f(x) = −x⁵ + 3x² + 4x + 8  và g(x) = −x⁵ − 3x² + 4x + 2. Chứng minh rằng đa thức f(x) – g(x) không có nghiệm.

Lời giải:

Ta có f(x) – g(x)

= (−x⁵ + 3x² + 4x + 8) – (−x⁵ − 3x² + 4x + 2)

= −x⁵ + 3x² + 4x + 8 + x⁵ + 3x² – 4x – 2

= (−x⁵ + x⁵) + (3x² + 3x²) + (4x – 4x) + (8 – 2)

= 6x² + 6

Vì f(x) – g(x) = 6x² + 6 ≥ 6 với mọi x nên f(x) – g(x) không có nghiệm.

Bài 7.37 trang 36 SBT Toán 7 Tập 2: Cho hai đa thức sau:

P(x) = 3x⁵ – 2x⁴ + 7x² + 3x – 10

Q(x) = –3x⁵ – x³ – 7x² + 2x + 10

a) Xác định bậc, hệ số cao nhất và hệ số tự do của các đa thức

S(x) = P(x) + Q(x) và D(x) = P(x) – Q(x)

b) Trong tập hợp {–1; 0; 1}, tìm những số là nghiệm của một trong hai đa thức S(x) và D(x).

Lời giải:

a) S(x) = P(x) + Q(x)

= (3x⁵ – 2x⁴ + 7x² + 3x – 10) + (–3x⁵ – x³ – 7x² + 2x + 10)

= 3x⁵ – 2x⁴ + 7x² + 3x – 10 – 3x⁵ – x³ – 7x² + 2x + 10

= (3x⁵ – 3x⁵) – 2x⁴ – x³ + (7x² – 7x²) + (3x + 2x) + (–10 + 10)

= –2x⁴ – x³ + 5x

S(x) = –2x⁴ – x³ + 5x là đa thức bậc 4 với hệ số cao nhất là –2 và hệ số tự do là 0.

D(x) = P(x) – Q(x)

= (3x⁵ – 2x⁴ + 7x² + 3x – 10) − (–3x⁵ – x³ – 7x² + 2x + 10)

= 3x⁵ – 2x⁴ + 7x² + 3x – 10 + 3x⁵ + x³ + 7x² – 2x – 10

= (3x⁵ + 3x⁵ ) – 2x⁴ + x³ + (7x² + 7x²)+ (3x – 2x) + (–10 – 10)

= 6x⁵ – 2x⁴ + x³  + 14x² + x – 20

D(x) = 6x⁵ – 2x⁴ + x³  + 14x² + x – 20 là đa thức bậc 5 với hệ số cao nhất là 6 và hệ số tự do là – 20

b) Xét đa thức S(x):

+) Thay x = – 1 vào đa thức S(x) ta được:

S(0) = –2.(– 1)⁴ – (– 1)³ + 5.(– 1) = – 6 ≠ 0

Do đó x = – 1 không là nghiệm của đa thức S(x).

+) Thay x = 0 vào đa thức S(x) ta được:

S(0) = –2.0⁴ – 0³ + 5.0 = 0

Do đó x = 0 là nghiệm của đa thức S(x).

+) Thay x = 1 vào đa thức S(x) ta được:

S(0) = –2.1⁴ – 1³ + 5.1 = 2 ≠ 0

Do đó x = 1 không là nghiệm của đa thức S(x).

Xét đa thức D(x):

+) Thay x = – 1 vào đa thức D(x) ta được:

D(1) = 6.(– 1)⁵ – 2.(– 1)⁴ + (– 1)³  + 14.(– 1)² + (– 1) – 20 = – 6 – 2 – 1 + 14 – 1 – 20 = – 16 ≠ 0.

Do đó x = – 1 không là nghiệm của đa thức D(x).

+) Thay x = 0 vào đa thức D(x) ta được:

D(1) = 6.0⁵ – 2.0⁴ + 0³  + 14.0² + 0 – 20 = – 20 ≠ 0

Do đó x = 0 không là nghiệm của đa thức D(x).

+) Thay x = 1 vào đa thức D(x) ta được:

D(1) = 6.1⁵ – 2.1⁴ + 1³  + 14.1² + 1 – 20 = 6 – 2 + 1 + 14 + 1 – 20 = 0

Do đó x = 1 là nghiệm của đa thức D(x).

Vậy x = 0 là nghiệm của đa thức S(x) và x = 1 là nghiệm của đa thức D(x).

Bài 7.38 trang 36 SBT Toán 7 Tập 2: Biết rằng đa thức f(x) = x⁴ + px³ – 2x² + 1  có hai nghiệm (khác 0) là hai số đối nhau. Chứng minh rằng p = 0.

Lời giải:

Gọi hai nghiệm đối nhau của f(x) là a và – a (a ≠ 0). Khi đó ta có:

f(a) = a⁴ + pa³ – 2a² + 1 = 0 = f(– a) = (– a)⁴ + p(–a)³ – 2(–a)² + 1

Suy ra:

a⁴ + pa³ – 2a² + 1 = a⁴ – pa³ – 2a² + 1

Thu gọn ta được pa³ = –pa³, suy ra 2pa³ = 0 . Do a ≠ 0 nên từ đẳng thức này suy ra p = 0.

Bài 7.39 trang 36 SBT Toán 7 Tập 2: Thực hiện các phép tính sau:

a) (5x³ – 2x² + 4x – 4)(3x² + x – 1);

b) (9x⁵ – 6x³ + 18x² – 35x – 42) : ( 3x³ + 5x + 6);

c) $\left[\left(6x^3-5x^2-8x+5\right)-(4x^2-6x+2)\right]$ : (2x – 3).

Lời giải:

a) (5x³ – 2x² + 4x – 4)(3x² + x – 1)

= 3x²(5x³ – 2x² + 4x – 4) + x(5x³ – 2x² + 4x – 4) – 1(5x³ – 2x² + 4x – 4)

= 15x⁵ – 6x⁴ + 12x³ – 12x² + 5x⁴ – 2x³ + 4x² – 4x – 5x³ + 2x² – 4x + 4

= 15x⁵ + (–6x⁴ + 5x⁴) + (12x³ – 2x³ – 5x³) + (–12x² + 4x² + 2x²)+ (–4x– 4x) + 4

= 15x⁵ – x⁴ + 5x³ – 6x² – 8x + 4

b) (9x⁵ – 6x³ + 18x² – 35x – 42) : ( 3x² + 5x + 6)

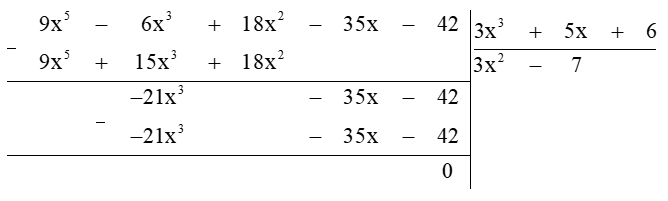
Vậy phép chia (9x⁵ – 6x³ + 18x² – 35x – 42) : ( 3x² + 5x + 6) có thương là 3x² − 7 và dư 0.

c) $\left[\left(6x^3-5x^2-8x+5\right)-(4x^2-6x+2)\right]$ : (2x – 3)

Tính (6x³ − 5x² − 8x + 5) − (4x² − 6x + 2)

= 6x³ − 5x² − 8x + 5 − 4x² + 6x − 2

= 6x³  + (−5x² − 4x²) + (−8x + 6x) + (5 − 2)

= 6x³  − 9x² − 2x  + 3

Ta thực hiện tiếp phép chia (6x³  − 9x² − 2x  + 3) : (2x – 3)

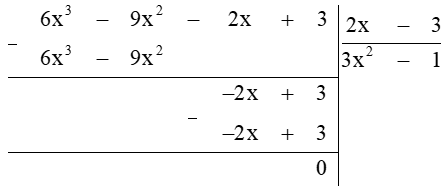
Vậy phép chia $\left[\left(6x^3-5x^2-8x+5\right)-(4x^2-6x+2)\right]$ : (2x – 3) có thương là 3x² − 1 và số dư là 0

Bài 7.40 trang 36 SBT Toán 7 Tập 2: Rút gọn các biểu thức sau:

a) A = (x − 1)(x + 2)(x − 3) − (x + 1)(x − 2)(x + 3)

b) B = (x − 1)(x + 1)( x² + 1)(x⁴ +1) − x⁸

Lời giải:

a) A = (x − 1)(x + 2)(x − 3) − (x + 1)(x − 2)(x + 3)

Ta có:

 (x − 1)(x + 2)(x − 3)

= [x(x + 2) − 1(x + 2)](x − 3)

= (x² + 2x − x − 2)(x − 3)

= (x² + x − 2)(x − 3)

= x(x² + x − 2) − 3(x² + x − 2)

= x³ + x² − 2x − 3x² − 3x + 6

= x³ + (x² − 3x²) +  (−2x − 3x) + 6

= x³ − 2x² − 5x + 6 (1)

(x + 1)(x − 2)(x + 3)

= [x(x − 2) + 1(x − 2)](x + 3)

= (x² − 2x + x − 2)(x + 3)

= (x² − x − 2)(x + 3)

= x(x² − x − 2) + 3(x² − x − 2)

= x³ − x² − 2x + 3x² − 3x − 6

= x³ + (−x² + 3x²) +  (−2x − 3x) − 6

= x³ + 2x² − 5x − 6 (2)

Khi đó: A = (x − 1)(x + 2)(x − 3) − (x + 1)(x − 2)(x + 3) = (1) − (2)

= (x³ − 2x² − 5x + 6) − (x³ + 2x² − 5x − 6)

= x³ − 2x² − 5x + 6 − x³ − 2x² + 5x + 6

= (x³ − x³) + (−2x² − 2x²) + (−5x + 5x) + (6 + 6)

= −4x² + 12.

b) B = (x − 1)(x + 1)( x² + 1)(x⁴ +1) − x⁸

Với M là một biểu thức tùy ý, ta có:

(M − 1)(M + 1) = M² − M + M − 1 hay (M − 1)(M + 1) = M² − 1  (1)

Từ đó, ta có:

(x − 1)(x + 1)  (áp dụng (1) với M = x)

(x² − 1)(x² + 1) = (x²)² − 1 = x⁴ − 1  (áp dụng (1) với M = x²)

(x⁴ − 1)(x⁴ + 1) = (x⁴)² − 1 = x⁸ − 1 (áp dụng (1) với M = x⁴).

Sử dụng các kết quả trên, ta được:

(x − 1)(x + 1)(x² + 1)(x⁴ + 1)

= $\left[(x-1)(x+1)\right]$ (x² +1)(x⁴ + 1)

= (x² − 1)(x² + 1)(x⁴  + 1)

= $\left[(x^2-1)(x^2+1)\right]$ (x⁴ + 1)

= (x⁴ − 1)(x⁴ + 1)

= x⁸ − 1.

Vậy B = (x − 1)(x + 1)( x² + 1)(x⁴ +1) − x⁸ = x⁸ – 1 − x⁸ = −1.

Xem thêm các bài giải sách bài tập Toán 7 Kết nối tri thức hay, chi tiết khác:

Giải SBT Toán 7 trang 35 Tập 2