Sách bài tập Toán 12 Bài 2 (Cánh diều): Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm

Trịnh Thị Thu Hiền Ngày: 30-10-2024 Lớp 12

Với giải sách bài tập Toán 12 Bài 2: Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 12. Mời các bạn đón xem:

Giải SBT Toán 12 Bài 2: Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm

Bài 9 trang 96 SBT Toán 12 Tập 1: Một mẫu số liệu ghép nhóm có độ lệch chuẩn bằng 9 thì có phương sai bằng bao nhiêu?

A. 9.

B. 3.

C. 18.

D. 81.

Lời giải:

Đáp án đúng là: D

Căn bậc hai số học của phương sai là độ lệch chuẩn, do đó phương sai bằng bình phương của độ lệch chuẩn.

Ta có 9² = 81.

Bài 10 trang 96 SBT Toán 12 Tập 1: Một mẫu số liệu ghép nhóm có phương sai bằng 16 thì độ lệch chuẩn bằng bao nhiêu?

A. 4.

B. 8.

C. 256.

D. 32.

Lời giải:

Đáp án đúng là: A

Căn bậc hai số học của phương sai là độ lệch chuẩn, ta có $\sqrt{16}$ = 4 nên độ lệch chuẩn của mẫu số liệu ghép nhóm trên là 4.

Vậy chọn A.

Bài 11 trang 96 SBT Toán 12 Tập 1: Một trung tâm ngoại ngữ thực hiện kiểm tra đầu vào của 80 học sinh đăng kí học, kết quả kiểm tra được cho bởi bảng tần số ghép nhóm như Bảng 17.

Một trung tâm ngoại ngữ thực hiện kiểm tra đầu vào của 80 học sinh đăng kí học

a) Tổng số học sinh là 800.
b) Số trung bình cộng của mẫu số liệu ghép nhóm đó là 5,7875.
c) Phương sai của mẫu số liệu ghép nhóm đó là: s² ≈ 3,85.
d) Độ lệch chuẩn của mẫu số liệu ghép nhóm đó là: s ≈ $\sqrt{3, 85}$ ≈ 1,962.

Lời giải:

a) S

b) Đ

c) Đ

d) Đ

Có tổng số 80 học sinh.

Số trung bình cộng của mẫu số liệu ghép nhóm ở bảng trên là:

$\bar{x}$ = $\frac{2.0, 5 + 3.1, 5 + 3.2, 5 + 5.3, 5 + 8.4, 5 + 20.5, 5 + 16.6, 5 + 15.7, 5 + 6.8, 5 + 2.9, 5}{80}$

= 5,7875.

Ta có phương sai của mẫu số liệu ghép nhóm trên là:

s² = $\frac{1}{80}$ .[2 . (0,5 – 5,7875)² + 3 . (1,5 – 5,7875)² + 3 . (2,5 – 5,7875)²

+ 5 . (3,5 – 5,7875)² + 8 . (4,5 – 5,7875)² + 20 .(5,5 – 5,7875)²

+ 16 . (6,5 – 5,7875)² + 15 . (7,5 – 5,7875)² + 6 . (8,5 – 5,7875)²

+ 2 . (9,5 – 5,7875)²] ≈ 3,85.

Độ lệch chuẩn của mẫu số liệu ghép nhóm trên là: s = $\sqrt{3, 85}$ ≈ 1,962.

Bài 12 trang 96 SBT Toán 12 Tập 1: Bảng 18 thống kê mật độ dân số (đơn vị: người/km²) của 23 tỉnh, thành phố thuộc vùng Trung du và miền núi phía Bắc, Đồng bằng sông Hồng (không kể thành phố Hà Nội và tỉnh Bắc Ninh) trong năm 2021. (Nguồn: Niên giám Thống kê 2021, NXB Thống kê, 2022).

Bảng 18 thống kê mật độ dân số (đơn vị: người/km2) của 23 tỉnh, thành phố thuộc vùng Trung du

a) Lập bảng tần số ghép nhóm của mẫu số liệu cho bởi Bảng 18 theo bảy nhóm:

[0; 200); [200; 400); [400; 600); [600; 800); [800; 1 000); [1 000; 1 200); [1 200; 1 400).

b) Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm đó (làm tròn đến kết quả hàng đơn vị).

Lời giải:

a) Ta có bảng tần số ghép nhóm như sau:

Bảng 18 thống kê mật độ dân số (đơn vị: người/km2) của 23 tỉnh, thành phố thuộc vùng Trung du

b) Số trung bình cộng của mẫu số liệu ghép nhóm trên là:

$\bar{x}$ = $\frac{11 . 100 + 2 . 300 + 2 . 500 + 1 . 700 + 1 . 900 + 4 . 1100 + 2 . 1300}{23}$ = $\frac{11300}{23}$ ≈ 491,3.

Ta có phương sai của mẫu số liệu ghép nhóm trên là:

s² = $\frac{1}{23}$ [ 11 . (100 – 491,3)² + 2 . (300 – 491,3)² + 2 . (500 – 491, 3)² + 1 . (700 – 491,3)²

+ 1 . (900 – 491,3)² + 4 . (1 100 – 491,3)² + 2 . (1 300 – 491,3)²]

≈ 206 880,9074 ≈ 206 881.

Độ lệch chuẩn của mẫu số liệu ghép nhóm trên là:

s = $\sqrt{206880, 9074}$ ≈ 455 (người/km²).

Lý thuyết Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm

1. Định nghĩa

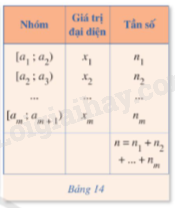
Xét mẫu số liệu ghép nhóm cho trong bảng sau:

Gọi $\bar{x}$ là số trung bình cộng của mẫu số liệu đó. Số:

$s^{2} = \frac{n_{1} {(x_{1} - \bar{x})}^{2} + . . . + n_{m} {(x_{m} - \bar{x})}^{2}}{n}$

được gọi là phương sai của mấu số liệu đó.

Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, là căn bậc hai số học của phương sai của mẫu số liệu ghép nhóm, tức là

s = \sqrt{s^{2}} .

Lý thuyết Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm (Cánh diều 2024) | Lý thuyết Toán 12 (ảnh 1)

2. Ý nghĩa

Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm là các xấp xỉ cho phương sai, độ lệch chuẩn của mẫu số liệu gốc, dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm đó.
Độ lệch chuẩn có cùng đơn vị với mẫu số liệu
Khi hai mẫu số liệu ghép nhóm có cùng đơn vị đo và có số trung bình cộng bằng nhau (hoặc xấp xỉ bằng nhau), mẫu số liệu nào có độ lệch chuẩn nhỏ hơn thì mức phân tán (so với số trung bình cộng) của các số liệu trong mẫu đó thấp hơn

Ví dụ: Anh An đầu tư số tiền bằng nhau vào hai lĩnh vực kinh doanh A, B. Anh An thống kê số tiền thu được mỗi tháng trong vòng 60 ngày theo mỗi lĩnh vực có kết quả như sau:

Lý thuyết Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm (Cánh diều 2024) | Lý thuyết Toán 12 (ảnh 2)

So sánh giá trị trung bình và độ lệch chuẩn của số tiền thu được mỗi tháng khi đầu tư vào mỗi lĩnh vực A, B. Đầu tư vào lĩnh vực nào “rủi ro” hơn?

Giải:

Chọn giá trị đại diện cho các nhóm số liệu ta có:

Lý thuyết Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm (Cánh diều 2024) | Lý thuyết Toán 12 (ảnh 3)

Số tiền trung bình thu được khi đầu tư vào các lĩnh vực A, B tương ứng là:

$\bar{x_{A}} = \frac{1}{60} (5.7, 5 + . . . + 5.27, 5) = 17, 5$ (triệu đồng)

$\bar{x_{B}} = \frac{1}{60} (20.7, 5 + . . . + 20.27, 5) = 17, 5$ (triệu đồng)

Như vậy, về trung bình đầu tư vào các lĩnh vực A, B số tiền thu được hàng tháng như nhau.

Độ lệch chuẩn của số tiền thu được hàng tháng khi đầu tư vào các lĩnh vực A, B tương ứng là:

$s_{A} = \sqrt{\frac{1}{60} (5.7, 5^{2} + . . . + 5.27, 5^{2} - 17, 5^{2}} = 5$

$s_{B} = \sqrt{\frac{1}{60} (20.7, 5^{2} + . . . + 20.27, 5^{2} - 17, 5^{2}} \approx 8, 42.$

Như vậy, độ lệch chuẩn của mẫu số liệu về số tiền thu được hàng tháng khi đầu tư vào lĩnh vực B cao hơn khi đầu tư vào lĩnh vực A. Người ta nói rằng, đầu tư vào lĩnh vực B là “rủi ro” hơn.

Xem thêm các bài giải SBT Toán lớp 12 Cánh diều hay, chi tiết khác:

Bài 1: Khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm

Bài 2: Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm

Bài tập cuối chương 3

Bài 1: Nguyên hàm

Bài 2: Nguyên hàm của một số hàm số sơ cấp

Bài 3: Tích phân