Với giải sách bài tập Toán 12 Bài 3: Biểu thức toạ độ của các phép toán vectơ sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 12. Mời các bạn đón xem:
Giải SBT Toán 12 Bài 3: Biểu thức toạ độ của các phép toán vectơ
Bài 18 trang 74 SBT Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho = (1; −3; −2), = (4; −1; 2). Tọa độ của vectơ là:
A. (3; 2; 4).
B. (5; −4; 0).
C. (−3; −2; −4).
D. (−3; −2; 0).
Lời giải:
Đáp án đúng là: C
Ta có: = (1 – 4; −3 – (−1); −2 – 2) = (−3; −2; −4).
Vậy = (−3; −2; −4).
Bài 19 trang 74 SBT Toán 12 Tập 1: Cho hai điểm A(2; 2; −1) và B(4; 6; −3). Tọa độ trung điểm M của đoạn thẳng AB là:
A. (3; 4; −2).
B. (6; 8; −4).
C. (1; 2; −1).
D. (−1; −2; 1).
Lời giải:
Đáp án đúng là: A
Ta có: M(x; y; z) với x = = 3; y = = 4; z = = −2.
Vậy M(3; 4; −2).
Bài 20 trang 74 SBT Toán 12 Tập 1: Cho tam giác ABC có A(1; 3; 2), B(2; −1; 1) và C(3; 1; 0). Tọa độ trọng tâm G của tam giác ABC là:
A. (6; 3; 3).
B. (2; 1; 1).
C. .
D. .
Lời giải:
Đáp án đúng là: B
Ta có G(x; y; z) với x = = 2; y = = 1; z = = 1.
Vậy G(2; 1; 1).
Bài 21 trang 74 SBT Toán 12 Tập 1: Trong không gian Oxyz, cho = (2; −1; 4). Độ dài vectơ bằng:
A. .
B. 5.
C. 27.
D. .
Lời giải:
Đáp án đúng là: D
Ta có: ||= .
Bài 22 trang 74 SBT Toán 12 Tập 1: Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(−2; −1; 4) và B(1; −3; −1). Độ dài đoạn thẳng AB bằng:
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: C
Ta có: = (1 – (−2); −3 – (−1); −1 – 4) = (3; −2; −5).
|| = = .
Bài 23 trang 74 SBT Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho = (0; 2; 2) và = (3; −3; 0). Góc giữa hai vectơ và bằng:
A. 60°.
B. 120°.
C. 150°.
D. 30°.
Lời giải:
Đáp án đúng là: B
Ta có: cos(,) = 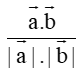
Suy ra (,) = 120°.
Bài 24 trang 74 SBT Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho A(1; 2; −1), B(2; −1; 3), C(−4; 7; 5).
|
a) Tọa độ của = (1; −3; 4), = (−5; 5; 6). |
|
|
|
b) AB = || = = AC = || = = . |
|
|
|
c) = 4. |
|
|
|
d) cos = . |
|
|
Lời giải:
|
a) Đ |
b) Đ |
c) Đ |
d) S |
Ta có: = (2 – 1; −1 – 2; 3 – (−1)) = (1; −3; 4),
= (−4 – 1; 7 – 2; 5 – (−1)) = (−5; 5; 6).
AB = || = = ,
AC = || = = .
Có: . = 1.(−5) + (−3).5 + 4.6 = 4.
cos = cos() = = = .
Bài 25 trang 75 SBT Toán 12 Tập 1: Cho hai vectơ = (3; −2; −5) và = (1; 1; 5). Hãy chỉ ra tọa độ của vectơ vuông góc với hai vectơ và .
Lời giải:
Ta có: = [,] = 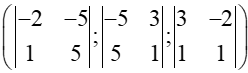
Khi đó, vectơ = (−5; −20; 5) vuông góc với cả hai vectơ và .
Bài 26 trang 75 SBT Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho M(2; 2; −2), N(−3; 5; 1), P(1; −1; −2).
a) Chứng minh ba điểm M, N, P không thẳng hàng.
b) Tính chu vi tam giác MNP.
c) Tính cos.
Lời giải:
a) Ta có: = (−3 – 2; 5 – 2; 1 – (−2)) = (−5; 3; 3),
= (1 – 2; −1 – 2; −2 – (−2)) = (−1; −3; 0).
Nhận thấy ≠ k với mọi k ∈ ℝ.
Vậy ba điểm M, N, P không thẳng hàng.
b) Ta có: = (1 – (−3); −1 – 5; −2 – 1) = (4; −6; −3).
MN = || = = ;
MP = || = = ;
NP = || = = .
Do đó, chu vi tam giác MNP là: + + .
c) Trong tam giác MNP, có:
cos = cos () = = = .
Bài 27 trang 75 SBT Toán 12 Tập 1: Rađa của một trung tâm kiểm soát không lưu sân bay có phạm vi theo dõi 500 km. Chọn hệ trục tọa độ Oxyz có gốc O trùng với vị trí của trung tâm kiểm soát không lưu, mặt phẳng (Oxy) trùng với mặt đất với trục Ox hướng về phía tây, trục Oy hướng về phía nam và trục Oz hướng thẳng đứng lên trời như Hình 18, trong đó đơn vị trên mỗi trục tính theo kilômét.
Hỏi rađa trung tâm kiểm soát không lưu có thể phát hiện được máy bay tại vị trí A có tọa độ (−200; 400; 200) đối với hệ trục tọa độ không?
Lời giải:
Khoảng cách từ trung tâm kiểm soát không lưu tới máy bay tại vị trí A bằng độ dài OA:
OA = || = = 200 < 500.
Vì vậy rađa trung tâm kiểm soát không lưu có thể phát hiện được máy bay tại vị trí A có tọa độ (−200; 400; 200).
Lý thuyết Biểu thức toạ độ của các phép toán vectơ
1. Biểu thức tọa độ của phép cộng hai vecto, phép trừ hai vecto, phép nhân một số với một vecto
|
Trong không gian Oxyz, cho hai vecto . và . Ta có: · · với k là một số thực |
2. Tọa độ trung điểm đoạn thẳng. Tọa độ trọng tâm tam giác
|
Trong không gian Oxyz, cho ba điểm không thẳng hàng . Khi đó: · Tọa độ trung điểm của đoạn thẳng AB là Tọa độ trọng tâm tam giác ABC là |
3. Biểu thức tọa độ của tích vô hướng
| Trong không gian Oxyz, tích vô hướng của hai vecto và được xác định bởi công thức |
4. Cách tìm tọa độ của một vecto vuông góc với hai vecto cho trước
|
Cho hai vecto và không cùng phương. Khi đó, vecto vuông góc với cả hai vecto và |
Xem thêm các bài giải SBT Toán lớp 12 Cánh diều hay, chi tiết khác: