Lý thuyết Biểu thức toạ độ của các phép toán vectơ (Chân trời sáng tạo 2024)

Lý thuyết Biểu thức toạ độ của các phép toán vectơ (Chân trời sáng tạo 2024) | Lý thuyết Toán 12

Admin Vietjack Ngày: 17-09-2024 Lớp 12

Với tóm tắt lý thuyết Toán lớp 12 Bài 3: Biểu thức toạ độ của các phép toán vectơ sách Chân trời sáng tạo hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12.

Lý thuyết Toán 12 Bài 3: Biểu thức toạ độ của các phép toán vectơ

A. Lý thuyết Biểu thức toạ độ của các phép toán vectơ

1. Biểu thức tọa độ của tổng, hiệu hai vecto và tích của một số với một vecto

Trong không gian Oxyz, cho hai vecto $\vec{a} = (x; y; z)$ và $\vec{b} = (x^{'}; y^{'}; z^{'})$ . Ta có:

$\vec{a} + \vec{b} = (x + x^{'}; y + y^{'}; z + z^{'})$
$\vec{a} - \vec{b} = (x - x^{'}; y - y^{'}; z - z^{'})$
$k \vec{a} = (k x; k y; k z)$ với k là một số thực

2. Biểu thức tọa độ của tích vô hướng

Trong không gian Oxyz, tích vô hướng của hai vecto $\vec{a} = (x; y; z)$ và $\vec{b} = (x^{'}; y^{'}; z^{'})$ được xác định bởi công thức $\vec{a} \cdot \vec{b} = x x^{'} + y y^{'} + z z^{'}$

3. Vận dụng

a) Xác định tọa độ của vecto khi biết tọa độ điểm đầu và điểm cuối

Trong không gian Oxyz, cho hai điểm $A (x_{A}; y_{A}; z_{A}), B (x_{B}; y_{B}; z_{B})$ . Ta có:

\vec{A B} = (x_{B} - x_{A}; y_{B} - y_{A}; z_{B} - z_{A})

b) Tọa độ trung điểm đoạn thẳng. Tọa độ trọng tâm tam giác

Trong không gian Oxyz, cho ba điểm không thẳng hàng $A (x_{A}; y_{A}; z_{A}), B (x_{B}; y_{B}; z_{B}), C (x_{C}; y_{C}; z_{C})$ . Khi đó:

Tọa độ trung điểm của đoạn thẳng AB là $(\frac{x_{A} + x_{B}}{2}; \frac{y_{A} + y_{B}}{2}; \frac{z_{A} + z_{B}}{2})$
Tọa độ trọng tâm tam giác ABC là $(\frac{x_{A} + x_{B} + x_{C}}{2}; \frac{y_{A} + y_{B} + y_{C}}{2}; \frac{z_{A} + z_{B} + z_{C}}{2})$

Sơ đồ tư duy Biểu thức toạ độ của các phép toán vectơ

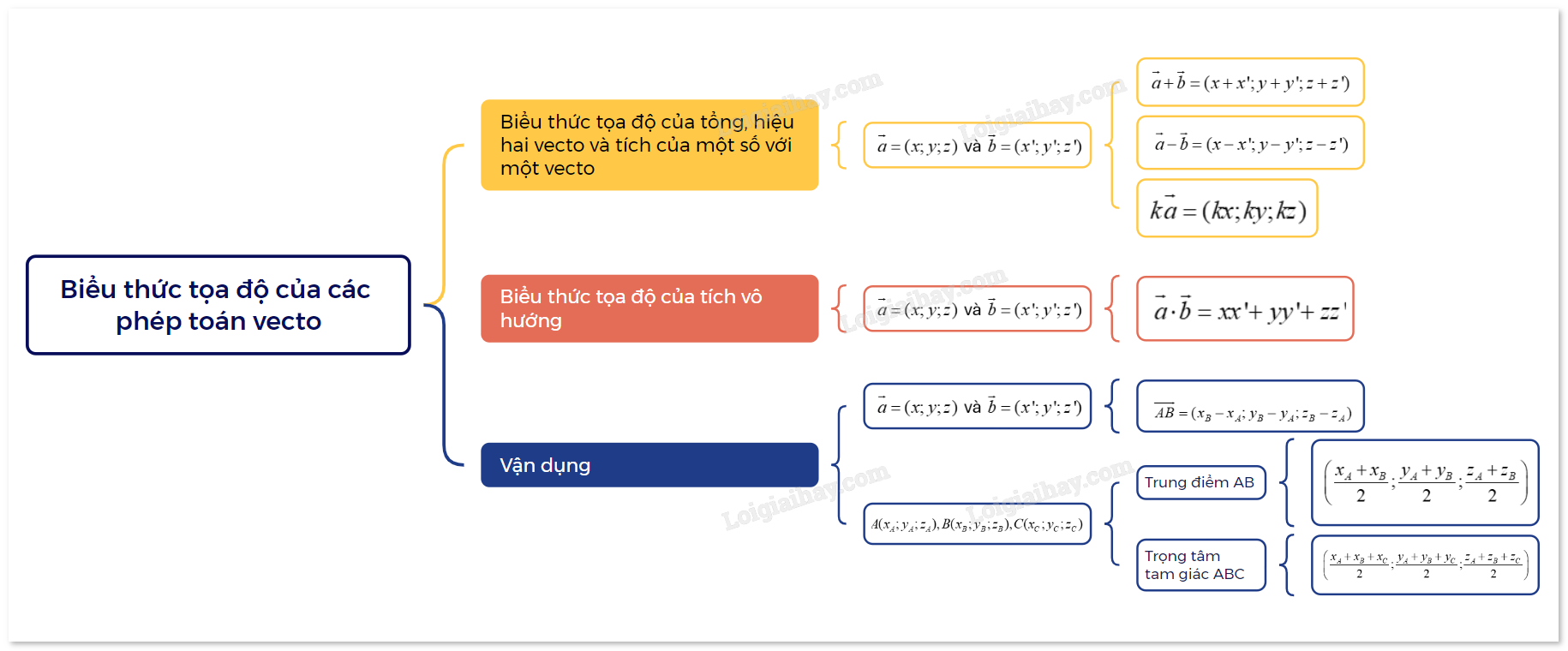
B. Bài tập Biểu thức toạ độ của các phép toán vectơ

Bài 1. Trong không gian Oxyz, cho điểm M(1; 2; 3). Tìm tọa độ hình chiếu M lên trục Ox.

A. (2; 0; 0).

B. (1; 0; 0).

C. (3; 0; 0).

D. (0; 2; 3).

Hướng dẫn giải

Đáp án đúng là: B

Tọa độ hình chiếu M lên trục Ox là (1; 0; 0).

Bài 2. Trong không gian Oxyz, cho hai vectơ $\vec{u} = (- 1; 3; - 2)$ và $\vec{v} = (2; 5; - 1)$ . Tìm tọa độ của vectơ $\vec{a} = 2 \vec{u} - 3 \vec{v}$ .

A. $\vec{a} = (- 8; 9; - 1)$ .

B. $\vec{a} = (- 8; - 9; 1)$ .

C. $\vec{a} = (8; - 9; - 1)$ .

D. $\vec{a} = (- 8; - 9; - 1)$ .

Hướng dẫn giải

Đáp án đúng là: D

Ta có $\vec{u} = (- 1; 3; - 2)$ $\Rightarrow 2 \vec{u} = (- 2; 6; - 4)$ ; $\vec{v} = (2; 5; - 1) \Rightarrow 3 \vec{v} = (6; 15; - 3)$ .

$\vec{a} = 2 \vec{u} - 3 \vec{v}$ = (−2 – 6; 6 – 15; −4 + 3) = (−8; −9; −1).

Bài 3. Trong không gian Oxyz, cho bốn điểm A(2; 0; 0), B(0; 2; 0), C(0; 0; 2) và D(2; 2; 2). Gọi M, N lần lượt là trung điểm của AB và CD. Tính độ dài MN.

Hướng dẫn giải

Vì M là trung điểm của AB nên $M (\frac{2 + 0}{2}; \frac{0 + 2}{2}; \frac{0 + 0}{2})$ hay M(1; 1; 0).

Vì N là trung điểm của CD nên $N (\frac{2 + 0}{2}; \frac{0 + 2}{2}; \frac{2 + 2}{2})$ hay N(1; 1; 2).

Ta có $M N = \sqrt{{(1 - 1)}^{2} + {(1 - 1)}^{2} + {(2 - 0)}^{2}} = 2$ .

Bài 4. Trong không gian Oxyz, cho tam giác ABC có A(1; 1; 1), B(5; 1; −2), C(7; 9; 1). Tính độ dài đường phân giác trong AD của góc A.

Hướng dẫn giải

Có $A B = \sqrt{{(5 - 1)}^{2} + {(1 - 1)}^{2} + {(- 2 - 1)}^{2}} = 5$ ; $A C = \sqrt{{(7 - 1)}^{2} + {(9 - 1)}^{2} + {(1 - 1)}^{2}} = 10$ .

Vì AD là đường phân giác trong của góc A nên $\frac{D B}{D C} = \frac{A B}{A C} = \frac{1}{2}$ mà D nằm giữa B, C nên $\vec{D C} = - 2 \vec{D B}$ .

Gọi D(x; y; z). Khi đó $\vec{D C} = (7 - x; 9 - y; 1 - z)$ > và $\vec{D B} = (5 - x; 1 - y; - 2 - z)$ .

Vì $\vec{D C} = - 2 \vec{D B}$ nên $\{\begin{cases} 7 - x = - 2 (5 - x) \\ 9 - y = - 2 (1 - y) \\ 1 - z = - 2 (- 2 - z) \end{cases}$ $\Leftrightarrow \{\begin{cases} x = \frac{17}{3} \\ y = \frac{11}{3} \\ z = - 1 \end{cases}$ . Suy ra $D (\frac{17}{3}; \frac{11}{3}; - 1)$ .

Do đó $A D = \sqrt{{(\frac{17}{3} - 1)}^{2} + {(\frac{11}{3} - 1)}^{2} + {(- 1 - 1)}^{2}} = \frac{2 \sqrt{74}}{3}$ .

Bài 5. Một công ty công nghệ đang phát triển một hệ thống định vị 3D để theo dõi các máy bay không người lái (drone) trong một khu vực cụ thể. Hệ thống này sử dụng ba trạm quan sát đặt tại các vị trí cố định để theo dõi vị trí của drone trong không gian Oxyz. Các trạm quan sát có tọa độ như sau: Trạm O₁: O₁(0; 0; 0), trạm O₂: O₂(10; 0; 0) và trạm O₃: O₃(0; 10; 0). Biết drone đang ở vị trí D(5; 5; 10).

a) Tính khoảng cách từ mỗi trạm quan sát đến drone.

b) Tính góc giữa các vectơ từ O₁ đến drone và từ O₂ đến drone.

Hướng dẫn giải

a) Ta có $O_{1} D = \sqrt{5^{2} + 5^{2} + 10^{2}} = 5 \sqrt{6}$ .

$O_{2} D = \sqrt{{(5 - 10)}^{2} + 5^{2} + 10^{2}} = 5 \sqrt{6}$ .

$O_{3} D = \sqrt{5^{2} + {(5 - 10)}^{2} + 10^{2}} = 5 \sqrt{6}$ .

b) Có $\vec{O_{1} D} = (5; 5; 10)$ , $\vec{O_{2} D} = (- 5; 5; 10)$ .

Do đó $\cos (\vec{O_{1} D}, \vec{O_{2} D}) = \frac{\vec{O_{1} D} . \vec{O_{2} D}}{|\vec{O_{1} D}| . |\vec{O_{2} D}|}$ $= \frac{5. (- 5) + 5.5 + 10.10}{5 \sqrt{6} .5 \sqrt{6}} = \frac{100}{150} = \frac{2}{3}$ .