Với giải Hoạt động khám phá 2 trang 70 Toán 12 Tập 1 Chân trời sáng tạo chi tiết trong Bài 1: Khoảng biến thiên và khoảng tử phân vị của mẫu số liệu ghép nhóm giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 12. Mời các bạn đón xem:
Giải bài tập Toán 12 Bài 1: Khoảng biến thiên và khoảng tử phân vị của mẫu số liệu ghép nhóm
Hoạt động khám phá 2 trang 70 Toán 12 Tập 1: Kết quả điều tra tổng thu nhập trong năm 2022 của một số hộ gia đình trong một địa phương được ghi lại ở bảng sau:
|
Tổng thu nhập (triệu đồng) |
[200; 250) |
[250; 300) |
[300; 350) |
[350; 400) |
[400; 450) |
|
Số hộ gia đình |
24 |
62 |
34 |
21 |
9 |
a) Hãy tìm các tứ phân vị Q1 và Q3.
b) Một doanh nghiệp địa phương muốn hướng dịch vụ của mình đến các gia đình có mức thu nhập ở tầm trung, tức là 50% các hộ gia đình có mức thu nhập ở chính giữa so với mức thu nhập của tất cả các hộ gia đình của địa phương. Hỏi doanh nghiệp cần hướng đến các gia đình có mức thu nhập trong khoảng nào?
Lời giải:
a) Số hộ gia đình được khảo sát (cỡ mẫu) là n = 24 + 62 + 34 + 21 + 9 = 150.
Gọi x1; x2; …; x150 là tổng thu nhập trong năm 2022 của 150 hộ gia đình được xếp theo thứ tự không giảm.
Ta có x1; x2; …; x24 ∈ [200; 250), x25; x26; …; x86 ∈ [250; 300),
x87; x88; …; x120 ∈ [300; 350), x121; …; x141 ∈ [350; 400), x142; …; x150 ∈ [400; 450).
Do đó, đối với dãy số liệu x1; x2; …; x150 thì
• Tứ phân vị thứ nhất Q1 là x38 ∈ [250; 300). Do đó, tứ phân thứ nhất của mẫu số liệu ghép nhóm là Q1 = 250 + .(300-250) = .
• Tứ phân vị thứ ba Q3 là x113 ∈ [300; 350). Do đó, tứ phân thứ ba của mẫu số liệu ghép nhóm là Q3 = 300 + . (350-300) = .
b) Doanh nghiệp cần hướng đến các gia đình có mức thu nhập trong khoảng [Q1; Q3) = 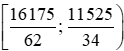
Xem thêm lời giải bài tập Toán lớp 12 Chân trời sáng tạo hay, chi tiết khác:
Xem thêm các bài giải bài tập Toán lớp 12 Chân trời sáng tạo hay, chi tiết khác:
Bài 1. Khoảng biến thiên và khoảng tử phân vị của mẫu số liệu ghép nhóm
Bài 2. Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm
Bài 1. Vẽ đồ thị hàm số bằng phần mềm Geogebra
Bài 2. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số bằng máy tính cầm tay