Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 12 Bài 1: Khoảng biến thiên và khoảng tử phân vị của mẫu số liệu ghép nhóm chi tiết sách Toán 12 Tập 1 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 12. Mời các bạn đón xem:

Giải bài tập Toán 12 Bài 1: Khoảng biến thiên và khoảng tử phân vị của mẫu số liệu ghép nhóm

Hoạt động khởi động trang 68 Toán 12 Tập 1: Biểu đồ dưới đây thống kê thời gian tập thể dục buổi sáng mỗi ngày trong tháng 9/2022 của bác Bình và bác An.

Ai là người có thời gian tập đều hơn?

Lời giải:

Sau bài học này, ta giải quyết được bài toán trên như sau:

Từ biểu đồ đã cho, ta có bảng thống kê sau:

Thời gian (phút)	[15; 20)	[20; 25)	[25; 30)	[30; 35)	[35; 40)
Số ngày tập của bác Bình	5	12	8	3	2
Số ngày tập của bác An	0	25	5	0	0

• Khoảng biến thiên của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bác Bình là 40 – 15 = 25 (phút).

Tuy nhiên, trong mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bác An, khoảng đầu tiên chứa dữ liệu là [20; 25) và khoảng cuối cùng chứa dữ liệu là [25; 30).

Do đó, khoảng biến thiên của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bác An là 30 – 20 = 10 (phút).

Nếu căn cứ theo khoảng biến thiên thì bác Bình có thời gian tập thể dục phân tán hơn bác An, vậy bác An là người có thời gian tập đều hơn.

• Cỡ mẫu n = 30.

- Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình:

Gọi x₁; x₂; …; x₃₀ là mẫu số liệu gốc về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình được xếp theo thứ tự không giảm.

Ta có x₁; x₂; …; x₅ ∈ [15; 20), x₆; x₇; …; x₁₇ ∈ [20; 25),

x₁₈; x₁₉; …; x₂₅ ∈ [25; 30), x₂₆; …; x₂₈ ∈ [30; 35), x₂₉; x₃₀ ∈ [35; 40).

Tứ phân vị thứ nhất Q₁ của mẫu số liệu gốc là x₈ ∈ [20; 25). Do đó, tứ phân thứ nhất của mẫu số liệu ghép nhóm là $Q_1=20+\frac{\frac{30}{4}-5}{12}\cdot \left(25-20\right)=\frac{505}{24}$ .

Tứ phân vị thứ ba Q₃ của mẫu số liệu gốc là x₂₃ ∈ [25; 30). Do đó, tứ phân thứ ba của mẫu số liệu ghép nhóm là $Q_3=25+\frac{\frac{3\cdot 30}{4}-\left(5+12\right)}{8}\cdot \left(30-25\right)=\frac{455}{16}$ .

Khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình là ∆_Q = Q₃ – Q₁ = $\frac{455}{16}-\frac{505}{24}=\frac{355}{48}$ .

- Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác An:

Gọi y₁; y₂; …; y₃₀ là mẫu số liệu gốc về thời gian tập thể dục buổi sáng mỗi ngày của bác An được xếp theo thứ tự không giảm.

Ta có y₁; y₂; …; y₂₅ ∈ [20; 25), y₂₆; …; y₂₉; y₃₀ ∈ [25; 30).

Tứ phân vị thứ nhất Q'₁ của mẫu số liệu gốc là y₈ ∈ [20; 25). Do đó, tứ phân thứ nhất của mẫu số liệu ghép nhóm là ${Q^{\text{'}}}_1=20+\frac{\frac{30}{4}}{25}\cdot \left(25-20\right)=\frac{43}{2}$ .

Tứ phân vị thứ ba Q'₃ của mẫu số liệu gốc là y₂₃ ∈ [20; 25). Do đó, tứ phân thứ ba của mẫu số liệu ghép nhóm là ${Q^{\text{'}}}_3=20+\frac{\frac{3\cdot 30}{4}}{25}\cdot \left(25-20\right)=\frac{49}{2}$ .

Khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác An là ∆'_Q = Q'₃ – Q'₁ = $\frac{49}{2}-\frac{43}{2}=3$ .

Vì ∆_Q = $\frac{355}{48}$ ≈ 7,4 > ∆'_Q = 3 nên khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình lớn hơn bác An.

Vậy nếu căn cứ theo khoảng tứ phân vị thì bác An là người có thời gian tập đều hơn.

1. Khoảng biến thiên

Hoạt động khám phá 1 trang 68 Toán 12 Tập 1: Bảng sau thống kê cân nặng của 50 quả xoài được lựa chọn ngẫu nhiên sau khi thu hoạch ở một nông trường.

Cân nặng (g)	[250; 290)	[290; 330)	[330; 370)	[370; 410)	[410; 450)
Số quả xoài	3	13	18	11	5

Có ý kiến cho rằng: “Trong 50 quả xoài trên, hiệu số cân nặng của hai quả bất kì không vượt quá 200 g”. Ý kiến đó đúng hay sai? Giải thích.

Lời giải:

Ý kiến nêu trên là đúng.

Giải thích: Quan sát bảng thống kê đã cho, ta thấy cân nặng lớn nhất quả xoài có thể đạt được là dưới 450 g, cân nặng nhỏ nhất quả xoài có thể đạt được là 250 g. Mà ta có 450 – 350 = 200. Do đó, hai quả bất kì nào cũng có hiệu số cân nặng không vượt quá 200 g.

Thực hành 1 trang 70 Toán 12 Tập 1: Bạn Trang thống kê lại chiều cao (đơn vị: cm) của các bạn học sinh nữ lớp 12C và lớp 12D ở bảng sau:

Chiều cao (cm)	[155; 160)	[160; 165)	[165; 170)	[170; 175)	[175; 180)	[180; 185)
Số học sinh nữ lớp 12C	2	7	12	3	0	1
Số học sinh nữ lớp 12D	5	9	8	2	1	0

Sử dụng khoảng biến thiên, hãy cho biết chiều cao của học sinh nữ lớp nào có độ phân tán lớn hơn.

Lời giải:

Khoảng biến thiên của mẫu số liệu ghép nhóm về chiều cao của các bạn học sinh nữ lớp 12C là: 185 – 155 = 30 (cm).

Trong mẫu số liệu ghép nhóm về chiều cao của các bạn học sinh nữ lớp 12D, khoảng đầu tiên chứa dữ liệu là [155; 160) và khoảng cuối cùng chứa dữ liệu là [175; 180).

Khoảng biến thiên của mẫu số liệu ghép nhóm về chiều cao của các bạn học sinh nữ lớp 12D là: 180 – 155 = 25 (cm).

Vậy nếu căn cứ theo khoảng biến thiên thì chiều cao của học sinh nữ lớp 12C có độ phân tán lớn hơn.

2. Khoảng tứ phân vị

Hoạt động khám phá 2 trang 70 Toán 12 Tập 1: Kết quả điều tra tổng thu nhập trong năm 2022 của một số hộ gia đình trong một địa phương được ghi lại ở bảng sau:

Tổng thu nhập (triệu đồng)	[200; 250)	[250; 300)	[300; 350)	[350; 400)	[400; 450)
Số hộ gia đình	24	62	34	21	9

a) Hãy tìm các tứ phân vị Q₁ và Q₃.

b) Một doanh nghiệp địa phương muốn hướng dịch vụ của mình đến các gia đình có mức thu nhập ở tầm trung, tức là 50% các hộ gia đình có mức thu nhập ở chính giữa so với mức thu nhập của tất cả các hộ gia đình của địa phương. Hỏi doanh nghiệp cần hướng đến các gia đình có mức thu nhập trong khoảng nào?

Lời giải:

a) Số hộ gia đình được khảo sát (cỡ mẫu) là n = 24 + 62 + 34 + 21 + 9 = 150.

Gọi x₁; x₂; …; x₁₅₀ là tổng thu nhập trong năm 2022 của 150 hộ gia đình được xếp theo thứ tự không giảm.

Ta có x₁; x₂; …; x₂₄ ∈ [200; 250), x₂₅; x₂₆; …; x₈₆ ∈ [250; 300),

x₈₇; x₈₈; …; x₁₂₀ ∈ [300; 350), x₁₂₁; …; x₁₄₁ ∈ [350; 400), x₁₄₂; …; x₁₅₀ ∈ [400; 450).

Do đó, đối với dãy số liệu x₁; x₂; …; x₁₅₀ thì

• Tứ phân vị thứ nhất Q₁ là x₃₈ ∈ [250; 300). Do đó, tứ phân thứ nhất của mẫu số liệu ghép nhóm là Q₁ = 250 + $\frac{\frac{150}{4}-24}{62}$.(300-250) = $\frac{16175}{62}$.

• Tứ phân vị thứ ba Q₃ là x₁₁₃ ∈ [300; 350). Do đó, tứ phân thứ ba của mẫu số liệu ghép nhóm là Q₃ = 300 + $\frac{\frac{3\cdot 150}{4}-\left(24+62\right)}{34}$. (350-300) = $\frac{11525}{34}$.

b) Doanh nghiệp cần hướng đến các gia đình có mức thu nhập trong khoảng [Q₁; Q₃) = 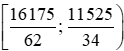 ≈ [260,89; 338,97) (triệu đồng).

Thực hành 2 trang 72 Toán 12 Tập 1: Hãy so sánh khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình và bác An trong Hoạt động khởi động.

Lời giải:

Ta có bảng thống kê sau:

Thời gian (phút)	[15; 20)	[20; 25)	[25; 30)	[30; 35)	[35; 40)
Số ngày tập của bác Bình	5	12	8	3	2
Số ngày tập của bác An	0	25	5	0	0

Cỡ mẫu n = 30.

• Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình:

Gọi x₁; x₂; …; x₃₀ là mẫu số liệu gốc về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình được xếp theo thứ tự không giảm.

Ta có x₁; x₂; …; x₅ ∈ [15; 20), x₆; x₇; …; x₁₇ ∈ [20; 25),

x₁₈; x₁₉; …; x₂₅ ∈ [25; 30), x₂₆; …; x₂₈ ∈ [30; 35), x₂₉; x₃₀ ∈ [35; 40).

Tứ phân vị thứ nhất Q₁ của mẫu số liệu gốc là x₈ ∈ [20; 25). Do đó, tứ phân thứ nhất của mẫu số liệu ghép nhóm là Q₁ = 20 + $\frac{\frac{30}{4}-5}{12}$.(25-20) = $\frac{505}{24}$.

Tứ phân vị thứ ba Q₃ của mẫu số liệu gốc là x₂₃ ∈ [25; 30). Do đó, tứ phân thứ ba của mẫu số liệu ghép nhóm là Q₃ = 25 + $\frac{\frac{3\cdot 30}{4}-\left(5+12\right)}{8}$. (30-25) = $\frac{455}{16}$.

Khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình là ∆_Q = Q₃ – Q₁ = $\frac{455}{16}-\frac{505}{24}=\frac{355}{48}$ .

• Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác An:

Gọi y₁; y₂; …; y₃₀ là mẫu số liệu gốc về thời gian tập thể dục buổi sáng mỗi ngày của bác An được xếp theo thứ tự không giảm.

Ta có y₁; y₂; …; y₂₅ ∈ [20; 25), y₂₆; …; y₂₉; y₃₀ ∈ [25; 30).

Tứ phân vị thứ nhất Q'₁ của mẫu số liệu gốc là y₈ ∈ [20; 25). Do đó, tứ phân thứ nhất của mẫu số liệu ghép nhóm là ${Q^{\text{'}}}_1=20+\frac{\frac{30}{4}}{25}\cdot \left(25-20\right)=\frac{43}{2}$ .

Tứ phân vị thứ ba Q'₃ của mẫu số liệu gốc là y₂₃ ∈ [20; 25). Do đó, tứ phân thứ ba của mẫu số liệu ghép nhóm là ${Q^{\text{'}}}_3=20+\frac{\frac{3\cdot 30}{4}}{25}\cdot \left(25-20\right)=\frac{49}{2}$ .

Khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác An là ∆'_Q = Q'₃ – Q'₁ = $\frac{49}{2}-\frac{43}{2}=3$ .

• Vì ∆_Q = $\frac{355}{48}$ ≈ 7,4 > ∆'_Q = 3 nên khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình lớn hơn bác An.

Thực hành 3 trang 73 Toán 12 Tập 1: a) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm ở Ví dụ 4 sau khi đã loại bỏ các giá trị ngoại lệ. Có nhận xét gì về khoảng biến thiên, khoảng tứ phân vị vừa tìm được và khoảng biến thiên, khoảng tứ phân vị ban đầu?

b) Hãy so sánh mức độ phân tán của hai mẫu số liệu chiều cao của các học sinh nữ lớp 12C và 12D ở Thực hành 1.

Lời giải:

a) Khoảng biến thiên của mẫu số liệu ghép nhóm ban đầu là:

R = 33 – 15 = 18 (phút).

Từ Ví dụ 4, ta có khoảng tứ phân vị của mẫu số liệu ghép nhóm ban đầu là ${\Delta }_Q=\frac{505}{114}$ .

Giá trị x trong mẫu số liệu là giá trị ngoại lệ nếu x > Q₃ + 1,5∆_Q hoặc x < Q₁ + 1,5∆_Q.

Hay x > $\frac{68}{3}+1,5\cdot \frac{505}{114}=\frac{6683}{228}\approx 29,31$ hoặc x < $\frac{693}{38}-1,5\cdot \frac{505}{114}=\frac{881}{76}\approx 11,59$ .

Do đó, chỉ có đúng 1 lần ông Thắng đi hết 32 phút là giá trị ngoại lệ của mẫu số liệu ghép nhóm.

Sau khi bỏ giá trị ngoại lệ, ta có bảng thống kê sau:

Thời gian (phút)	[15; 18)	[18; 21)	[21; 24)	[24; 27)	[27; 30)
Số lần	22	38	27	8	4

Khoảng biến thiên của mẫu số liệu ghép nhóm sau khi loại bỏ giá trị ngoại lệ là:

R' = 30 – 15 = 15 (phút).

Cỡ mẫu n' = 99.

Gọi y₁; y₂; y₃; …; y₉₉ là mẫu số liệu gốc gồm thời gian 99 lần đi xe buýt của ông Thắng được xếp theo thứ tự không giảm.

Ta có: y₁; …; y₂₂ ∈ [15; 18); y₂₃; …; y₆₀ ∈ [18; 21); y₆₁; …; y₈₇ ∈ [21; 24);

   y₈₈; …; y₉₅ ∈ [24; 27); y₉₅; …; y₉₉ ∈ [27; 30).

Tứ phân vị thứ nhất của mẫu số liệu gốc là y_25­ ∈ [18; 21). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm sau khi loại bỏ giá trị ngoại lệ là:

${Q^{\text{'}}}_1=18+\frac{\frac{99}{4}-22}{38}\cdot \left(21-18\right)=\frac{2769}{152}$.

Tứ phân vị thứ ba của mẫu số liệu gốc là y_75­ ∈ [21; 24). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm sau khi loại bỏ giá trị ngoại lệ là:

${Q^{\text{'}}}_3=21+\frac{\frac{3\cdot 99}{4}-\left(22+38\right)}{27}\cdot \left(24-21\right)=\frac{271}{12}$.

Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm sau khi loại bỏ giá trị ngoại lệ là:

${{\Delta }^{\text{'}}}_Q={Q^{\text{'}}}_3-{Q^{\text{'}}}_1=\frac{271}{12}-\frac{2769}{152}=\frac{1991}{456}\approx 4,37$.

Nhận xét: Sau khi loại bỏ giá trị ngoại lệ, khoảng biến thiên giảm mạnh, còn khoảng tứ phân vị mới không bị ảnh hưởng nhiều.

b)

• Lớp 12C:

Cỡ mẫu n = 2 + 7 + 12 + 3 + 0 + 1 = 25.

Gọi x₁; x₂; …; x₂₅ là mẫu số liệu gốc về chiều cao của 25 học sinh nữ lớp 12C được xếp theo thứ tự không giảm.

Ta có x₁; x₂ ∈ [155; 160), x₃; x₄; …; x₉ ∈ [160; 165),

   x₁₀; x₁₁; …; x₂₁ ∈ [165; 170), x₂₂; …; x₂₄ ∈ [170; 175), x₂₅ ∈ [180; 185).

Tứ phân vị thứ nhất của mẫu số liệu gốc là $\frac{1}{2}$ (x₆ + x₇) ∈ [160; 165). Do đó, tứ phân thứ nhất của mẫu số liệu ghép nhóm là:

$Q_1=160+\frac{\frac{25}{4}-2}{7}\cdot \left(165-160\right)=\frac{4565}{28}$.

Tứ phân vị thứ ba của mẫu số liệu gốc là $\frac{1}{2}$ (x₁₉ + x₂₀) ∈ [165; 170). Do đó, tứ phân thứ ba của mẫu số liệu ghép nhóm là:

$Q_3=165+\frac{\frac{3\cdot 25}{4}-\left(2+7\right)}{12}\cdot \left(170-165\right)=\frac{2705}{16}$.

Khoảng tứ phân vị của mẫu số liệu ghép nhóm về chiều cao của các bạn học sinh nữ lớp 12C là:

∆_Q = Q₃ – Q₁ = $\frac{2705}{16}-\frac{4565}{28}=\frac{675}{112}$ ≈ 6,03.

• Lớp 12D:

Cỡ mẫu n' = 5 + 9 + 8 + 2 + 1 = 25.

Gọi y₁; y₂; …; y₂₅ là mẫu số liệu gốc về chiều cao của 25 học sinh nữ lớp 12D được xếp theo thứ tự không giảm.

Ta có y₁; y₂; …; y­₅ ∈ [155; 160), y₆; y₇; …; y₁₄ ∈ [160; 165),

   y₁₅; y₁₆; …; y₂₂ ∈ [165; 170), y₂₃; y₂₄ ∈ [170; 175), y₂₅ ∈ [175; 180).

Tứ phân vị thứ nhất của mẫu số liệu gốc là $\frac{1}{2}$ (y₆ + y₇) ∈ [160; 165). Do đó, tứ phân thứ nhất của mẫu số liệu ghép nhóm là:

${Q^{\text{'}}}_1=160+\frac{\frac{25}{4}-5}{9}\cdot \left(165-160\right)=\frac{5785}{36}$.

Tứ phân vị thứ ba của mẫu số liệu gốc là $\frac{1}{2}$ (y₁₉ + y₂₀) ∈ [165; 170). Do đó, tứ phân thứ ba của mẫu số liệu ghép nhóm là:

${Q^{\text{'}}}_3=165+\frac{\frac{3\cdot 25}{4}-\left(5+9\right)}{8}\cdot \left(170-165\right)=\frac{5375}{32}$.

Khoảng tứ phân vị của mẫu số liệu ghép nhóm về chiều cao của các bạn học sinh nữ lớp 12D là:

∆'_Q = Q'₃ – Q'₁ = $\frac{5375}{32}-\frac{5785}{36}=\frac{2095}{288}$ ≈ 7,27.

Vì ∆'_Q ≈ 7,27 > ∆_Q ≈ 6,03 nên chiều cao của các bạn học sinh nữ lớp 12D có độ phân tán lớn hơn lớp 12C.

Vận dụng trang 73 Toán 12 Tập 1: Giả sử kết quả khảo sát hai khu vực A và B về độ tuổi kết hôn của một số phụ nữ vừa lập gia đình được cho ở bảng sau:

Tuổi kết hôn	[19; 22)	[22; 25)	[25; 28)	[28; 31)	[31; 34)
Số phụ nữ khu vực A	10	27	31	25	7
Số phụ nữ khu vực B	47	40	11	2	0

a) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của từng mẫu số liệu ghép nhóm ứng với mỗi khu vực A và B.

b) Nếu so sánh theo khoảng tứ phân vị thì phụ nữ ở khu vực nào có độ tuổi kết hôn đồng đều hơn?

Lời giải:

a)

• Khu vực A:

Khoảng biến thiên của mẫu số liệu ghép nhóm ứng với khu vực A là:

R = 34 – 19 = 15.

Cỡ mẫu n = 10 + 27 + 31 + 25 + 7 = 100.

Gọi x₁; x₂; …; x₁₀₀ là mẫu số liệu gốc về độ tuổi kết hôn của một số phụ nữ vừa lập gia đình ở khu vực A được xếp theo thứ tự không giảm.

Ta có x₁; x₂; …; x₁₀ ∈ [19; 22), x₁₁; x₁₂; …; x₃₇ ∈ [22; 25),

   x₃₈; x₃₉; …; x₆₈ ∈ [25; 28), x₆₉; …; x₉₃ ∈ [28; 31), x₉₄; …; x₁₀₀ ∈ [31; 34).

Tứ phân vị thứ nhất của mẫu số liệu gốc là $\frac{1}{2}$ (x₂₅ + x₂₆) ∈ [22; 25). Do đó, tứ phân thứ nhất của mẫu số liệu ghép nhóm là:

$Q_1=22+\frac{\frac{100}{4}-10}{27}\cdot \left(25-22\right)=\frac{71}{3}$.

Tứ phân vị thứ ba của mẫu số liệu gốc là $\frac{1}{2}$ (x₇₅ + x₇₆) ∈ [28; 31). Do đó, tứ phân thứ ba của mẫu số liệu ghép nhóm là:

$Q_3=28+\frac{\frac{3\cdot 100}{4}-\left(10+27+31\right)}{25}\cdot \left(31-28\right)=\frac{721}{25}$.

Khoảng tứ phân vị của mẫu số liệu ghép nhóm về độ tuổi kết hôn của một số phụ nữ vừa lập gia đình ở khu vực A là:

∆_Q = Q₃ – Q₁ = $\frac{721}{25}-\frac{71}{3}=\frac{388}{75}$ ≈ 5,17.

• Khu vực B:

Khoảng biến thiên của mẫu số liệu ghép nhóm ứng với khu vực B là:

R' = 31 – 19 = 12.

Cỡ mẫu n' = 47 + 40 + 11 + 2 = 100.

Gọi y₁; y₂; …; y₁₀₀ là mẫu số liệu gốc về độ tuổi kết hôn của một số phụ nữ vừa lập gia đình ở khu vực B được xếp theo thứ tự không giảm.

Ta có y₁; y₂; …; y­₄₇ ∈ [19; 22), y₄₈; y₄₉; …; y₈₇ ∈ [22; 25),

   y₈₈; y₈₉; …; y₉₈ ∈ [25; 28), y₉₉; y₁₀₀ ∈ [28; 31).

Tứ phân vị thứ nhất của mẫu số liệu gốc là $\frac{1}{2}$ (y₂₅ + y₂₆) ∈ [19; 22). Do đó, tứ phân thứ nhất của mẫu số liệu ghép nhóm là:

${Q^{\text{'}}}_1=19+\frac{\frac{100}{4}}{47}\cdot \left(22-19\right)=\frac{968}{47}$.

Tứ phân vị thứ ba của mẫu số liệu gốc là $\frac{1}{2}$ (y₇₅ + y₇₆) ∈ [22; 25). Do đó, tứ phân thứ ba của mẫu số liệu ghép nhóm là:

${Q^{\text{'}}}_3=22+\frac{\frac{3\cdot 100}{4}-47}{40}\cdot \left(25-22\right)=\frac{241}{10}$.

Khoảng tứ phân vị của mẫu số liệu ghép nhóm về độ tuổi kết hôn của một số phụ nữ vừa lập gia đình ở khu vực B là:

∆'_Q = Q'₃ – Q'₁ = $\frac{241}{10}-\frac{968}{47}=\frac{1647}{470}$ ≈ 3,5.

Vì ∆'_Q < ∆_Q nên phụ nữ ở khu vực B có độ tuổi kết hôn đồng đều hơn.

Bài tập

Bài 1 trang 73 Toán 12 Tập 1: Bảng sau thống kê lượng mưa (đơn vị: mm) đi được vào tháng 7 từ năm 2002 đến 2021 tại một trạm quan trắc đặt ở Cà Mau.

341,4	187,1	242,2	522,9	251,4	432,2	200,7	388,6	258,4	288,5
298,1	413,5	413,5	332	421	475	400	305	520	147

(Nguồn: Tổng cục Thống kê)

a) Hãy tìm khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu trên.

b) Hãy chia mẫu số liệu trên thành 4 nhóm với nhóm đầu tiên là [140; 240) và lập bảng tần số ghép nhóm.

c) Hãy tìm khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm và so sánh với kết quả tương ứng thu được ở câu a).

Lời giải:

a) Sắp xếp lại mẫu số liệu trên theo thứ tự không giảm, ta được:

147  187,1  200,7  242,2  251,4  258,4  288,5

298,1  305  332  341,4  388,6  400  413,5

413,5  421  432,2  475  520  522,9

Khoảng biến thiên của mẫu số liệu trên là:

R = 522,9 – 147 = 375,9 (mm).

Cỡ mẫu n = 20.

Tứ phân vị thứ nhất là trung vị của mẫu số liệu:

147; 187,1; 200,7; 242,2; 251,4; 258,4 ; 288,5; 298,1; 305 ; 332.

Do đó, $Q_1=\frac{251,4+258,4}{2}=254,9$ .

Tứ phân vị thứ ba là trung vị của mẫu số liệu:

341,4; 388,6 ; 400; 413,5; 413,5 ; 421; 432,2; 475; 520; 522,9.

Do đó, $Q_3=\frac{413,5+421}{2}=417,25$ .

Khoảng tứ phân vị của mẫu số liệu đã cho là:

∆_Q = Q₃ – Q₁ = 417,25 – 254,9 = 162,35.

b) Nhóm đầu tiên là [140; 240), ta chọn 3 nhóm còn lại là

[240; 340), [340; 440), [440; 540).

Từ bảng thống kê ban đầu, ta lập được bảng tần số ghép nhóm như sau:

Lượng mưa (mm)	[140; 240)	[240; 340)	[340; 440)	[440; 540)
Số tháng	3	7	7	3

c) Cỡ mẫu n = 20.

Khoảng biến thiên của mẫu số liệu ghép nhóm là

R' = 540 – 140 = 400 (mm).

Gọi x₁; x₂; …; x₂₀ là mẫu số liệu gốc về lượng mưa đo được vào tháng 7 từ năm 2002 đến 2021 tại một trạm quan trắc đặt ở Cà Mau được xếp theo thứ tự không giảm.

Ta có x₁; x₂; x₃ ∈ [140; 240), x₄; …; x₁₀ ∈ [240; 340),

   x₁₁; …; x₁₇ ∈ [340; 440), x₁₈; x₁₉; x₂₀ ∈ [440; 540).

Tứ phân vị thứ nhất của mẫu số liệu gốc là ∈ [240; 340).

Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:

${Q^{\text{'}}}_1=240+\frac{\frac{20}{4}-3}{7}\left(340-240\right)=\frac{1880}{7}$.

Tứ phân vị thứ ba của mẫu số liệu gốc là $\frac{1}{2}\left(x_{15}+x_{16}\right)$ ∈ [340; 440).

Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:

${Q^{\text{'}}}_3=340+\frac{\frac{3\cdot 20}{4}-\left(3+7\right)}{7}\left(440-340\right)=\frac{2880}{7}$.

Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:

∆'_Q = Q'₃ – Q'₁ = $\frac{2880}{7}-\frac{1880}{7}=\frac{1000}{7}$ ≈ 142,86.

Ta thấy khoảng biến thiên của mẫu số liệu ghép nhóm lớn hơn mẫu số liệu đã cho; khoảng tứ phân vị của mẫu số liệu ghép nhóm nhỏ hơn mẫu số liệu đã cho.

Bài 2 trang 74 Toán 12 Tập 1: Biểu đồ dưới đây biểu diễn số lượt khách hàng đặt bàn qua hình thức trực tuyến mỗi ngày trong quý III năm 2022 của một nhà hàng. Cột thứ nhất biểu diễn số ngày có từ 1 đến dưới 6 lượt đặt bàn; cột thứ hai biểu diễn số ngày có từ 6 đến dưới 11 lượt đặt bàn; …

Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm cho bởi biểu đồ trên.

Bài 3 trang 74 Toán 12 Tập 1: Kết quả đo chiều cao của 100 cây keo 3 năm tuổi tại một nông trường được cho ở bảng sau:

Chiều cao (m)	[8,4; 8,6)	[8,6; 8,8)	[8,8; 9,0)	[9,0; 9,2)	[9,2; 9,4)
Số cây	5	12	25	44	14

a) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.

b) Trong 100 cây keo trên có 1 cây cao 8,4 m. Hỏi chiều cao của cây keo này có phải là giá trị ngoại lệ không?

Lời giải:

a) Khoảng biến thiên của mẫu số liệu ghép nhóm là:

R = 9,4 – 8,4 = 1 (m).

Cỡ mẫu n = 100.

Gọi x₁; x₂; …; x₁₀₀ là mẫu số liệu gốc về chiều cao của 100 cây keo 3 năm tuổi tại một nông trường được xếp theo thứ tự không giảm.

Ta có x₁; …; x₅ ∈ [8,4; 8,6), x₆; …; x₁₇ ∈ [8,6; 8,8), x_18­; …; x₄₂ ∈ [8,8; 9,0),

   x₄₃; …; x₈₆ ∈ [9,0; 9,2), x₈₇; …; x₁₀₀ ∈ [9,2; 9,4).

Tứ phân vị thứ nhất của mẫu số liệu gốc là $\frac{1}{2}\left(x_{25}+x_{26}\right)$ ∈ [8,8; 9,0).

Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:

$Q_1=8,8+\frac{\frac{100}{4}-\left(5+12\right)}{25}\left(9,0-8,8\right)=8,864$.

Tứ phân vị thứ ba của mẫu số liệu gốc là $\frac{1}{2}\left(x_{75}+x_{76}\right)$ ∈ [9,0; 9,2).

Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:

$Q_3=9,0+\frac{\frac{3\cdot 100}{4}-\left(5+12+25\right)}{44}\left(9,2-9,0\right)=9,15$.

Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:

∆_Q = Q₃ – Q₁ = 9,15 – 8,864 = 0,286.

b) Trong 100 cây keo trên có 1 cây cao 8,4 m thuộc nhóm [8,4; 8,6).

Vì Q₁ – 1,5∆_Q = 8,864 – 1,5 ∙ 0,286 = 8,435 > 8,4 nên chiều cao của cây keo cao 8,4 m là giá trị ngoại lệ của mẫu số liệu ghép nhóm.

Lời giải:

Từ biểu đồ đã cho, ta có có bảng thống kê sau:

Số lượt đặt bàn	[1; 6)	[6; 11)	[11; 16)	[16; 21)	[21; 26)
Số ngày	14	30	25	18	5

Cỡ mẫu n = 14 + 30 + 25 + 18 + 5 = 92.

Gọi x₁; x₂; …; x₉₂ là mẫu số liệu gốc về số lượt khách đặt bàn qua hình thức trực tuyến mỗi ngày trong quý III năm 2022 của một nhà hàng được xếp theo thứ tự không giảm.

Ta có x₁; …; x₁₄ ∈ [1; 6), x₁₅; …; x₄₄ ∈ [6; 11), x_45­; …; x₆₉ ∈ [11; 16),

   x₇₀; …; x₈₇ ∈ [16; 21), x₈₈; …; x₉₂ ∈ [21; 26).

Tứ phân vị thứ nhất của mẫu số liệu gốc là $\frac{1}{2}\left(x_{23}+x_{24}\right)$ ∈ [6; 11).

Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:

$Q_1=6+\frac{\frac{92}{4}-14}{30}\left(11-6\right)=\frac{15}{2}$ = 7,5.

Tứ phân vị thứ ba của mẫu số liệu gốc là $\frac{1}{2}\left(x_{69}+x_{70}\right)$ .

Mà x₆₉ ∈ [11; 16) và x₇₀ ∈ [16; 21)

Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là Q₃ = 16.

Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:

∆_Q = Q₃ – Q₁ = 16 – 7,5 = 8,5.

Bài 4 trang 74 Toán 12 Tập 1: Kết quả đo chiều cao của 100 cây keo 3 năm tuổi tại một nông trường được cho ở bảng sau:

Chiều cao (m)	[8,4; 8,6)	[8,6; 8,8)	[8,8; 9,0)	[9,0; 9,2)	[9,2; 9,4)
Số cây	5	12	25	44	14

a) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.

b) Trong 100 cây keo trên có 1 cây cao 8,4 m. Hỏi chiều cao của cây keo này có phải là giá trị ngoại lệ không?

Lời giải:

a) Khoảng biến thiên của mẫu số liệu ghép nhóm là:

R = 9,4 – 8,4 = 1 (m).

Cỡ mẫu n = 100.

Gọi x₁; x₂; …; x₁₀₀ là mẫu số liệu gốc về chiều cao của 100 cây keo 3 năm tuổi tại một nông trường được xếp theo thứ tự không giảm.

Ta có x₁; …; x₅ ∈ [8,4; 8,6), x₆; …; x₁₇ ∈ [8,6; 8,8), x_18­; …; x₄₂ ∈ [8,8; 9,0),

   x₄₃; …; x₈₆ ∈ [9,0; 9,2), x₈₇; …; x₁₀₀ ∈ [9,2; 9,4).

Tứ phân vị thứ nhất của mẫu số liệu gốc là $\frac{1}{2}\left(x_{25}+x_{26}\right)$ ∈ [8,8; 9,0).

Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:

$Q_1=8,8+\frac{\frac{100}{4}-\left(5+12\right)}{25}\left(9,0-8,8\right)=8,864$.

Tứ phân vị thứ ba của mẫu số liệu gốc là $\frac{1}{2}\left(x_{75}+x_{76}\right)$ ∈ [9,0; 9,2).

Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:

$Q_3=9,0+\frac{\frac{3\cdot 100}{4}-\left(5+12+25\right)}{44}\left(9,2-9,0\right)=9,15$.

Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:

∆_Q = Q₃ – Q₁ = 9,15 – 8,864 = 0,286.

b) Trong 100 cây keo trên có 1 cây cao 8,4 m thuộc nhóm [8,4; 8,6).

Vì Q₁ – 1,5∆_Q = 8,864 – 1,5 ∙ 0,286 = 8,435 > 8,4 nên chiều cao của cây keo cao 8,4 m là giá trị ngoại lệ của mẫu số liệu ghép nhóm.

Bài 5 trang 74 Toán 12 Tập 1: Hai bảng tần số ghép nhóm dưới đây thống kê theo độ tuổi số lượng thành viên nam và thành viên nữ đang sinh hoạt trong một câu lạc bộ dưỡng sinh.

a) Hãy tính các khoảng tứ phân vị của tuổi nam giới và nữ giới trong mỗi bảng số liệu ghép nhóm trên.

b) Hãy cho biết trong câu lạc bộ trên, nam giới hay nữ giới có tuổi đồng đều hơn.

Lời giải:

a)

• Nam giới:

Cỡ mẫu n = 4 + 7 + 4 + 6 + 15 + 12 + 2 = 50.

Gọi x₁; x₂; …; x₅₀ là mẫu số liệu gốc về tuổi của nam giới đang sinh hoạt trong câu lạc bộ dưỡng sinh được xếp theo thứ tự không giảm.

Ta có x₁; …; x₄ ∈ [50; 55), x₅; …; x₁₁ ∈ [55; 60), x_12­; …; x₁₅ ∈ [60; 65),

   x₁₆; …; x₂₁ ∈ [65; 70), x₂₂; …; x₃₆ ∈ [70; 75), x₃₇; …; x₄₈ ∈ [75; 80),

   x₄₉; x₅₀ ∈ [80; 85).

Tứ phân vị thứ nhất của mẫu số liệu gốc là x₁₃ ∈ [60; 65).

Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:

$Q_1=60+\frac{\frac{50}{4}-\left(4+7\right)}{4}\left(65-60\right)=61,875$.

Tứ phân vị thứ ba của mẫu số liệu gốc là x₃₈ ∈ [75; 80).

Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:

$Q_3=75+\frac{\frac{3\cdot 50}{4}-\left(4+7+4+6+15\right)}{12}\left(80-75\right)=75,625$.

Khoảng tứ phân vị của mẫu số liệu ghép nhóm về tuổi của nam giới đang sinh hoạt trong câu lạc bộ dưỡng sinh là:

∆_Q = Q₃ – Q₁ = 75,625 – 61,875 = 13,75.

• Nữ giới:

Cỡ mẫu n' = 3 + 4 + 5 + 3 + 7 + 14 + 13 + 1 = 50.

Gọi y₁; y₂; …; y₅₀ là mẫu số liệu gốc về tuổi của nữ giới đang sinh hoạt trong câu lạc bộ dưỡng sinh được xếp theo thứ tự không giảm.

Ta có y₁; …; y₄ ∈ [50; 55), y₄; …; y₇ ∈ [55; 60), y_8­; …; y₁₂ ∈ [60; 65),

   y₁₃; …; x₁₅ ∈ [65; 70), y₁₆; …; y₂₂ ∈ [70; 75), y₂₃; …; y₃₆ ∈ [75; 80),

   y₃₇; …; y₄₉ ∈ [80; 85), y₅₀ ∈ [85; 90).

Tứ phân vị thứ nhất của mẫu số liệu gốc là y₁₃ ∈ [65; 70).

Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:

${Q^{\text{'}}}_1=65+\frac{\frac{50}{4}-\left(3+4+5\right)}{3}\left(70-65\right)=\frac{395}{6}$.

Tứ phân vị thứ ba của mẫu số liệu gốc là y₃₈ ∈ [80; 85).

Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:

${Q^{\text{'}}}_3=80+\frac{\frac{3\cdot 50}{4}-\left(3+4+5+3+7+14\right)}{13}\left(85-80\right)=\frac{2095}{26}$.

Khoảng tứ phân vị của mẫu số liệu ghép nhóm về tuổi của nữ giới đang sinh hoạt trong câu lạc bộ dưỡng sinh là:

∆'_Q = Q'₃ – Q'₁ = $\frac{2095}{26}-\frac{395}{6}=\frac{575}{39}$ ≈ 14,74.

b) Ta có ∆'_Q ≈ 14,74 > ∆_Q = 13,75 nên trong câu lạc bộ dưỡng sinh, nam giới có tuổi đồng đều hơn.

Xem thêm các bài giải bài tập Toán lớp 12 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương II

Bài 1. Khoảng biến thiên và khoảng tử phân vị của mẫu số liệu ghép nhóm

Bài 2. Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm

Bài tập cuối chương III

Bài 1. Vẽ đồ thị hàm số bằng phần mềm Geogebra

Bài 2. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số bằng máy tính cầm tay

Lý thuyết Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm

1. Khoảng biến thiên

a) Định nghĩa

Khoảng biến thiên, kí hiệu R, của mẫu số liệu ghép nhóm là hiệu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên có chứa dữ liệu của mẫu số liệu. $R=u_{k+1}-u_1$

b) Ý nghĩa

- Khoảng biến thiên của mẫu số liệu ghép nhóm xấp xỉ cho khoảng biến thiên của mẫu số liệu gốc và có thể dùng để đo mức độ phân tán của mẫu số liệu

- Khoảng biến thiên chưa phản ánh đầy đủ mức độ phân tán của phần lớn các  số liệu. Hơn nữa giá trị của R thường tăng vọt khi xuất hiện giá trị ngoại lệ trong mẫu số liệu. Do đó, để phản ánh mức độ phân tán của số liệu, người ta còn dùng các số đặc trưng khác

2. Khoảng tứ phân vị

a) Định nghĩa

Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu ${\mathrm{\Delta }}_Q$, là hiệu giữa tứ phân vị thứ ba $Q_3$ và tứ phân vị thứ nhất $Q_1$ của mẫu số liệu ghép nhóm đó, tức là: ${\mathrm{\Delta }}_Q=Q_3-Q_1$

b) Ý nghĩa

b) Ý nghĩa

- Khoảng tứ phân vị của mẫu số liệu ghép nhóm xấp xỉ khoảng tứ phân vị của mẫu số liệu gốc và là một đại lượng cho biết mức độ phân tán của nửa giữa mẫu số liệu.

- Khoảng tứ phân vị của mẫu số liệu ghép nhóm càng nhỏ thì dữ liệu càng tập trung xung quanh trung vị.

- Khoảng tứ phân vị được dùng để xác định giá trị ngoại lệ trong mẫu số liệu. Giá trị x trong mẫu số liệu là giá trị ngoại lệ nếu $x>Q_3+1,5\mathrm{\Delta }Q$ hoặc $x<Q_1-1,5\mathrm{\Delta }Q$.

- Khoảng tứ phân vị của mẫu số liệu ghép nhóm không bị ảnh hưởng nhiều bởi các giá trị ngoại lệ trong mẫu số liệu.