Bài 2.37 trang 74 Toán 12 Tập 1 Kết nối tri thức | Giải bài tập Toán 12

Bài 2.37 trang 74 Toán 12 Tập 1 Kết nối tri thức | Giải bài tập Toán 12

Trịnh Thị Thu Hiền Ngày: 29-03-2024 Lớp 12

193

Với giải Bài 2.37 trang 74 Toán 12 Tập 1 Kết nối tri thức chi tiết trong Bài tập cuối chương 2 trang 73 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 12. Mời các bạn đón xem:

Giải bài tập Toán 12 Bài tập cuối chương 2 trang 73

Bài 2.37 trang 74 Toán 12 Tập 1: Cho hình hộp ABCD.A’B’C’D’, gọi G là trọng tâm của tam giác BDA’.
a) Biểu diễn $\vec{A G}$ theo $\vec{A B}, \vec{A D}$ và $\vec{A A^{'}}$ .
b) Từ câu a, hãy chứng tỏ ba điểm A, G và C’ thẳng hàng.

Lời giải:

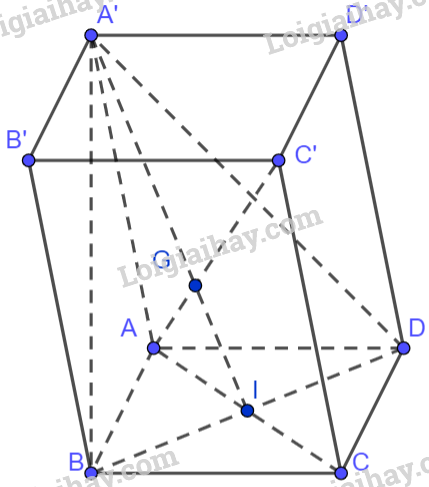
Tài liệu VietJack

Gọi I là giao điểm của AC và BD. Vì tứ giác ABCD là hình bình hành nên I là trung điểm của BD. Do đó, A’I là đường trung tuyến của tam giác A’BD. Mà G là trọng tâm tam giác A’BD nên $\vec{A^{'} G} = \frac{2}{3} \vec{A^{'} I}$ .

Vì I là trung điểm BD nên:

$\vec{A^{'} I} = \frac{1}{2} (\vec{A^{'} B} + \vec{A^{'} D}) = \frac{1}{2} (\vec{A^{'} A} + \vec{A^{'} B^{'}} + \vec{A^{'} D^{'}} + \vec{A^{'} A}) = - \vec{A A^{'}} + \frac{1}{2} \vec{A B} + \frac{1}{2} \vec{A D}$

Do đó, $\vec{A^{'} G} = - \frac{2}{3} \vec{A A^{'}} + \frac{1}{3} \vec{A B} + \frac{1}{3} \vec{A D}$

Ta có: $\vec{A G} = \vec{A A^{'}} + \vec{A^{'} G} = \vec{A A^{'}} - \frac{2}{3} \vec{A A^{'}} + \frac{1}{3} \vec{A B} + \frac{1}{3} \vec{A D} = \frac{1}{3} (\vec{A A^{'}} + \vec{A B} + \vec{A D})$

b) Vì ABCD.A’B’C’D’ là hình hộp nên $\vec{A C^{'}} = \vec{A A^{'}} + \vec{A B} + \vec{A D}$

Do đó, $\vec{A C^{'}} = 3 \vec{A G}$ nên hai vectơ $\vec{A C^{'}}$ và $\vec{A G}$ cùng phương. Vậy ba điểm A, G và C’ thẳng hàng.

Xem thêm lời giải bài tập Toán lớp 12 Kết nối tri thức hay, chi tiết khác:

Bài 2.25 trang 73 Toán 12 Tập 1: Cho tứ diện ABCD. Lấy G là trọng tâm của tam giác BCD. Khẳng định nào sau đây là sai?.......

Bài 2.26 trang 73 Toán 12 Tập 1: Cho hình hộp ABCD.A’B’C’D’. Lấy M là trung điểm của đoạn thẳng CC’. Vectơ $\vec{A M}$ bằng.......

Bài 2.27 trang 73 Toán 12 Tập 1: Cho hình hộp ABCD.A’B’C’D’. Khẳng định nào dưới đây là sai?.......

Bài 2.28 trang 73 Toán 12 Tập 1: Cho tứ diện đều ABCD có độ dài cạnh bằng a, gọi M là trung điểm của đoạn thẳng CD. Tích vô hướng $\vec{A B} . \vec{A M}$ bằng......

Bài 2.29 trang 73 Toán 12 Tập 1: Trong không gian Oxyz, cho $\vec{a} = (1; - 2; 2), \vec{b} = (- 2; 0; 3)$ . Khẳng định nào dưới đây là sai?......

Bài 2.30 trang 73 Toán 12 Tập 1: Trong không gian Oxyz, cho hình bình hành ABCD có $A (- 1; 0; 3), B (2; 1; - 1)$ và $C (3; 2; 2)$ . Tọa độ của điểm D là.......

Bài 2.31 trang 73 Toán 12 Tập 1: Trong không gian Oxyz, cho $A (1; 0; - 1), B (0; - 1; 2)$ và $G (2; 1; 0)$ . Biết tam giác ABC có trọng tâm G. Tọa độ của điểm C là......

Bài 2.32 trang 73 Toán 12 Tập 1: Trong không gian Oxyz, cho $\vec{a} = (2; 1; - 3), \vec{b} = (- 2; - 1; 2)$ . Tích vô hướng $\vec{a} . \vec{b}$ bằng......

Bài 2.33 trang 73 Toán 12 Tập 1: Trong không gian Oxyz, cho $\vec{a} = (2; 1; - 2), \vec{b} = (0; - 1; 1)$ . Góc giữa hai vectơ $\vec{a}, \vec{b}$ bằng......

Bài 2.34 trang 74 Toán 12 Tập 1: Trong không gian Oxyz, cho $\vec{a} = (- 2; 2; 2), \vec{b} = (1; - 1; - 2)$ . Côsin của góc giữa hai vectơ $\vec{a}, \vec{b}$ bằng.......

Bài 2.35 trang 74 Toán 12 Tập 1: Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật. Chứng minh rằng: $\vec{S A} + \vec{S C} = \vec{S B} + \vec{S D}$ ........

Bài 2.36 trang 74 Toán 12 Tập 1: Cho tứ diện ABCD, lấy hai điểm M, N thỏa mãn $\vec{M B} + 2 \vec{M A} = \vec{0}$ và $\vec{N C} = 2 \vec{D N}$ . Hãy biểu diễn $\vec{M N}$ theo $\vec{A D}$ và $\vec{B C}$ .......

Bài 2.37 trang 74 Toán 12 Tập 1: Cho hình hộp ABCD.A’B’C’D’, gọi G là trọng tâm của tam giác BDA’......

Bài 2.38 trang 74 Toán 12 Tập 1: Trong không gian Oxyz, cho các điểm $A (2; - 1; 3), B (1; 1; - 1)$ và $C (- 1; 0; 2)$ .....

Bài 2.39 trang 74 Toán 12 Tập 1: Trong không gian Oxyz, cho hình hộp OABC.O’A’B’C’ và các điểm $A (2; 3; 1), C (- 1; 2; 3)$ và $O^{'} (1; - 2; 2)$ . Tìm tọa độ các đỉnh còn lại của hình hộp......

Bài 2.40 trang 74 Toán 12 Tập 1: Trong không gian Oxyz, cho hai vectơ $\vec{a} = (- 2; 1; 2), \vec{b} = (1; 1; - 1)$ ....

Bài 2.41 trang 74 Toán 12 Tập 1: Trong không gian Oxyz, cho các điểm $A (4; 2; - 1), B (1; - 1; 2)$ và $C (0; - 2; 3)$ .....

Bài 2.42 trang 74 Toán 12 Tập 1: Hình 2.53 minh họa một chiếc đèn được treo cách trần nhà 0,5m, cách hai tường lần lượt là 1,2m và 1,6m. Hai bức tường vuông góc với nhau và cùng vuông góc với trần nhà. Người ta di chuyển chiếc đèn đó đến vị trí mới cách trần nhà là 0,4m, cách hai tường đều là 1,5m......

Xem thêm các bài giải bài tập Toán lớp 12 Kết nối tri thức hay, chi tiết khác:

Bài 8. Biểu thức toạ độ của các phép toán vectơ

Bài tập cuối chương 2

Bài 9. Khoảng biến thiên và khoảng tứ phân vị

Bài 10. Phương sai và độ lệch chuẩn

Bài tập cuối chương 3

Khảo sát và vẽ đồ thị hàm số với phần mềm GeoGebra

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

162

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

135

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

112

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

108

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.