Với giải HĐ2 trang 61 Toán 12 Tập 1 Kết nối tri thức chi tiết trong Bài 7: Hệ trục toạ độ trong không gian giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 12. Mời các bạn đón xem:
Giải bài tập Toán 12 Bài 7: Hệ trục toạ độ trong không gian
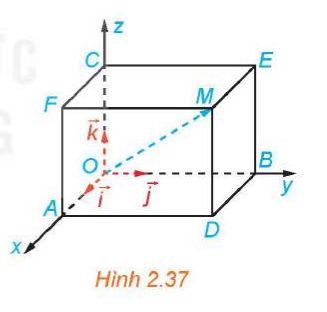
HĐ2 trang 61 Toán 12 Tập 1: Trong không gian Oxyz, cho một điểm M không thuộc các mặt phẳng tọa độ. Vẽ hình hộp chữ nhật OADB.CFME có ba đỉnh A, B, C lần lượt thuộc các tia Ox, Oy, Oz (H.2.37).
a) Hai vectơ và có bằng nhau hay không?
b) Giải thích vì sao có thể viết với x, y, z là các số thực.
Lời giải:
a) Vì OADB.CFME là hình hộp chữ nhật nên theo quy tắc hình hộp ta có:
b) Vì là vectơ đơn vị trên trục Ox nên với x là số thực.
Vì là vectơ đơn vị trên trục Oy nên với y là số thực.
Vì là vectơ đơn vị trên trục Oz nên với z là số thực.
Do đó, với x, y, z là các số thực.
Xem thêm lời giải bài tập Toán lớp 12 Kết nối tri thức hay, chi tiết khác:
Luyện tập 3 trang 62 Toán 12 Tập 1: Trong Ví dụ 3, hãy xác định tọa độ của các điểm B, D và C’......
Xem thêm các bài giải bài tập Toán lớp 12 Kết nối tri thức hay, chi tiết khác:
Bài 7. Hệ trục toạ độ trong không gian
Bài 8. Biểu thức toạ độ của các phép toán vectơ
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
