Với lời giải Toán 11 trang 114 Tập 2 chi tiết trong Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối sách Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải Toán 11 Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối

Luyện tập 5 trang 114 Toán 11 Tập 2: Cho khối tứ diện đều ABCD cạnh a. Chứng minh rằng thể tích của khối tứ diện đó bằng $\frac{a^3\sqrt{2}}{12}.$

Lời giải:

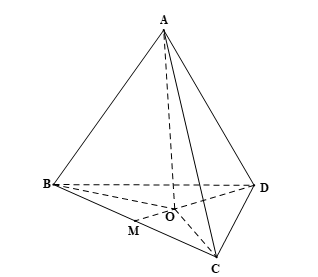
Gọi M là trung điểm của BC, O là trọng tâm tam giác BCD.

Vì ABCD là hình tứ diện đều nên BCD là tam giác đều.

Mà O là trọng tâm tam giác BCD nên O cũng là tâm đường tròn ngoại tiếp tam giác BCD.

Do đó AO ⊥ (BCD).

Xét tam giác đều BCD có: DM là đường trung tuyến (do M là trung điểm của BC) cũng đồng thời là đường cao của tam giác nên DM ⊥ BC.

Do M là trung điểm của BC nên $MC=\frac{BC}{2}=\frac{a}{2}.$

Áp dụng định lí Pythagore vào tam giác DMC vuông tại M (do DM ⊥ BC) có:

DC² = DM² + MC²

Do đó $DM=\sqrt{D{C}^2-M{C}^2}=\sqrt{a^2-{\left(\frac{a}{2}\right)}^2}=\frac{a\sqrt{3}}{2}.$

Vì O là trọng tâm tam giác BCD nên $OD=\frac{2}{3}DM=\frac{2}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}.$

Do AO ⊥ (BCD) và DO ⊂ (BCD) nên AO ⊥ DO, do đó tam giác ADO vuông tại O.

Áp dụng định lí Pythagore vào tam giác ADO vuông tại O có:

AD² = AO² + DO²

Suy ra $AO=\sqrt{A{D}^2-D{O}^2}=\sqrt{a^2-{\left(\frac{a\sqrt{3}}{3}\right)}^2}=\sqrt{a^2-\frac{a^2}{3}}=\sqrt{\frac{2a^2}{3}}=\frac{a\sqrt{6}}{3}.$

Diện tích tam giác BCD đều có đường cao DM là:

$S_{\Delta BCD}=\frac{1}{2}.DM.BC=\frac{1}{2}.\frac{a\sqrt{3}}{2}.a=\frac{a^2\sqrt{3}}{4}$ (đvdt).

Thể tích của khối tứ diện đều ABCD cạnh a có chiều cao $AO=\frac{a\sqrt{6}}{3}$ và diện tích đáy $S_{\Delta BCD}=\frac{a^2\sqrt{3}}{4}$là:

$V_{ABCD}=\frac{1}{3}{S}_{\Delta BCD}.AO=\frac{1}{3}.\frac{a^2\sqrt{3}}{4}.\frac{a\sqrt{6}}{3}=\frac{a^3\sqrt{2}}{12}$ (đvtt)

Luyện tập 6 trang 114 Toán 11 Tập 2: Một thùng đựng rác có dạng khối chóp cụt tứ giác đều với hai cạnh đáy lần lượt dài 2 dm và 3 dm, chiều cao bằng 4 dm. Tính thể tích của thùng đựng rác.

Lời giải:

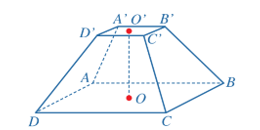
Một thùng đựng rác có dạng khối chóp cụt tứ giác đều nên ta có hai đáy là hình vuông.

Diện tích đáy lớn là S₁ = 3² = 9 (dm²).

Diện tích đáy bé là S₂ = 2² = 4 (dm²).

Vậy thể tích của thùng đựng rác có dạng khối chóp cụt tứ giác đều có chiều cao bằng 4 dm diện tích đáy hai đáy S₁ = 9 dm², S₂ = 4 dm² là:

$V=\frac{1}{3}h\left(S_1+\sqrt{S_1{S}_2}+S_2\right)=\frac{1}{3}\mathrm{.4.}\left(9+\sqrt{9.4}+4\right)=\frac{76}{3}$(dm³).