Với lời giải Toán 11 trang 35 Tập 2 chi tiết trong Bài tập cuối chương 6 trang 34 sách Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải Toán 11 Bài tập cuối chương 6 trang 34
Bài 11 trang 35 Toán 11 Tập 2: Biết 4α + 4−α = 5. Tính giá trị biểu thức
a )2α + 2−α;
b )42α + 4−2α .
Lời giải:
a) Ta có
.
Vậy .
b) Ta có
.
Vậy .
Bài 12 trang 35 Toán 11 Tập 2: Tính giá trị của biểu thức :
a) ;
b) ;
c) .
Lời giải:
a )
;
b)
;
c)
.
Lời giải:
Ta có 5x = 3 ⇔ x = log5 3 và 3y = 5 ⇔ y = log3 5.
Do đó .
Bài 14 trang 35 Toán 11 Tập 2: Viết công thức biểu thị y theo x, biết
.
Lời giải:
Ta có
.
Bài 15 trang 35 Toán 11 Tập 2: Giải các phương trình sau:
a);
b);
c) ;
d).
Lời giải:
a)
.
Vậy phương trình đã cho có nghiệm .
b)
Vậy phương trình đã cho có nghiệm x = 6.
c) ĐKXĐ: x – 2 > 0 ⇔ x > 2.
Khi đó:
Vậy phương trình đã cho có nghiệm x = 5.
d)ĐKXĐ:
Khi đó:
Vậy phương trình đã cho có nghiệm .
Bài 16 trang 35 Toán 11 Tập 2: Giải các bất phương trình :
a);
b) ;
c).
Lời giải:
a)
(do )
Vậy bất phương trình đã cho có nghiệm x < 1.
b)
(do 3 > 1)
.
Vậy bất phương trình đã cho có nghiệm .
c)ĐKXĐ:
Khi đó:
.
Kết hợp với điều kiện ta được nghiệm của bất phương trình .
a) Công thức P(t) = P0.at cho phép tính số lượng vi khuẩn của mẻ nuôi cấy sau t ngày kể từ thời điểm ban đầu. Xác định các tham số P0 và a (a > 0). Làm tròn a đến hàn phần trăm.
b) Sau 5 ngày thì số lượng vi khuẩn bằng bao nhiêu? Làm tròn kết quả đến hàng trăm.
c) Sau bao nhiêu ngày thì số lượng vi khuẩn vượt gấp đôi số lượng ban đầu? Làm tròn kết quả đến hàng phần mười.
Lời giải:
a) Ban đầu có 1000 vi khuẩn nên P0=1000.
Sau 2 ngày, số lượng vi khuẩn là:
P=125% . P0=125%.1000=1250
Ta có:P(2)=P0.a2⇔1250=1000.a2
⇔a2=1,25⇔a≈1,12.
b) Số lượng vi khuẩn sau 5 ngày là:
P(5)=P0.a5=1000.1,122≈1800(vi khuẩn).
c) Với P(t)=2P0, ta có:
P(t)=P0.at⇔2P0=P0.1,12t
⇔1,12t=2⇔t=log1,122≈6,1(ngày)
Vậy sau 6,1 ngày thì số lượng vi khuẩn vượt gấp đôi số lượng ban đầu.
a) Dung dịch acid A có độ pH bằng 1,9; dung dịch B có độ pH bằng 2,5. Dung dịch nào có độ acid cao hơn và cao hơn bao nhiêu lần?
b) Nước cất có nồng độ H+ là 10–7 mol/L. Nước chảy từ một vòi nước có độ pH từ 6,5 đến 6,7 thì có độ acid cao hay thấp hơn nước cất.
Lời giải:
a)• pHA=1,9⇔−log[H+]=1,9
⇔log[H+]=−1,9⇔H+=10−1,9.
Vậy độ acid của dung dịch A là 10−1,9 mol/L.
• pHB=2,5⇔−log[H+]=2,5
⇔log[H+]=−2,5⇔H+=10−2,5.
Vậy độ acid của dung dịch B là 10−2,5mol/L.
Ta có: .
Vậy độ acid của dung dịch A cao hơn độ acid của dung dịch B 3,98 lần.
b) Ta có:6,5<pH<6,7⇔6,5<−log[H+]<6,7
⇔−6,5>log[H+]>−6,7⇔10−6,5>H+>10−6,7.
Do đó nước chảy từ vòi nước có độ acid từ 10−6,7mol/L đến 10−6,5mol/L.
Vậy nước đó có độ acid cao hơn nước cất.
Xem thêm các lời giải bài tập Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 1 trang 34 Toán 11 Tập 2: Rút gọn biểu thức 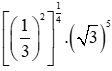
Bài 2 trang 34 Toán 11 Tập 2: Nếu 2α = 9 thì có giá trị bằng...
Bài 3 trang 34 Toán 11 Tập 2: Nếu thì...
Bài 4 trang 34 Toán 11 Tập 2: Nếu thì 3x có giá trị bằng...
Bài 5 trang 34 Toán 11 Tập 2: Cho α, β là hai số thực với α < β. Khẳng định nào sau đây đúng?...
Bài 6 trang 34 Toán 11 Tập 2: Hình nào vẽ đồ thị của hàm số ?...
Bài 7 trang 34 Toán 11 Tập 2: Phương trình có nghiệm là...
Bài 8 trang 34 Toán 11 Tập 2: Tập nghiệm của bất phương trình 0,53x1>0,25 là...
Bài 9 trang 34 Toán 11 Tập 2: Nếu thì...
Bài 10 trang 34 Toán 11 Tập 2: Số nguyên dương nhỏ nhất thỏa mãn là...
Bài 11 trang 35 Toán 11 Tập 2: Biết 4α + 4−α = 5. Tính giá trị biểu thức...
Bài 12 trang 35 Toán 11 Tập 2: Tính giá trị của biểu thức...
Bài 14 trang 35 Toán 11 Tập 2: Viết công thức biểu thị y theo x, biết...
Bài 15 trang 35 Toán 11 Tập 2: Giải các phương trình sau:...
Bài 16 trang 35 Toán 11 Tập 2: Giải các bất phương trình...
Xem thêm các bài giải SGK Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác: