Với lời giải Toán 11 trang 34 Tập 2 chi tiết trong Bài tập cuối chương 6 trang 34 sách Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải Toán 11 Bài tập cuối chương 6 trang 34
Bài 1 trang 34 Toán 11 Tập 2: Rút gọn biểu thức 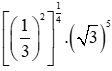
A. .
B. .
C. .
D. 9.
Lời giải:
Đáp án đúng là: D
.
Bài 2 trang 34 Toán 11 Tập 2: Nếu 2α = 9 thì có giá trị bằng
A. .
B. 3.
C. .
D. .
Lời giải:
Đáp án đúng là: A
.
Bài 3 trang 34 Toán 11 Tập 2: Nếu thì
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: B
.
Bài 4 trang 34 Toán 11 Tập 2: Nếu thì 3x có giá trị bằng
A. 6.
B. 8.
C. 16.
D. 64.
Lời giải:
Đáp án đúng là: B
Ta có
⇔ 3x = 8.
Bài 5 trang 34 Toán 11 Tập 2: Cho α, β là hai số thực với α < β. Khẳng định nào sau đây đúng?
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: C
• Xét phương án A.
Do 0 < 0,3 < 1 nên hàm số y = 0,3x nghịch biến trên ℝ.
Mà α < β nên (0,3)α < (0,3)β.
• Xét phương án B.
Do π > 1 nên hàm số y = πx đồng biến trên ℝ.
Mà α < β nên πα < πβ.
• Xét phương án C.
Do nên hàm số đồng biến trên ℝ.
Mà α < β nên .
• Xét phương án D.
Do nên hàm số đồng biến trên ℝ.
Mà α < β nên.
Bài 6 trang 34 Toán 11 Tập 2: Hình nào vẽ đồ thị của hàm số ?
A.
B.
C.
D.
Lời giải:
Đáp án đúng là: D
− Hàm số nghịch biến trên (0; +∞). Loại A, C.
− Giới hạn: . Loại B.
Bài 7 trang 34 Toán 11 Tập 2: Phương trình có nghiệm là
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: A
.
Bài 8 trang 34 Toán 11 Tập 2: Tập nghiệm của bất phương trình 0,53x1>0,25 là
A. (−∞; 1).
B. (1; +∞).
C. (0; 1).
D. .
Lời giải:
Đáp án đúng là: A
0,53x−1>0,25⇔0,53x−1>0,52
⇔3x−1<2(do 0<0,5<1)
⇔3x<3⇔x<1.
Vậy tập nghiệm của bất phương trình là (−∞;1).
Bài 9 trang 34 Toán 11 Tập 2: Nếu thì
A. x = 8.
B. x = 23.
C. x = 12,5.
D. x = 5.
Lời giải:
Đáp án đúng là: C
ĐKXĐ: x > 0
Khi đó:
.
Bài 10 trang 34 Toán 11 Tập 2: Số nguyên dương nhỏ nhất thỏa mãn là
A. x = 0.
B. x = 1.
C. x = −5.
D. x = −4.
Lời giải:
Đáp án đúng là: D
ĐKXĐ: .
Khi đó:
Kết hợp với điều kiện ta được nghiệm của bất phương trình là
Vậy số nguyên x nhỏ nhất thỏa mãn là x = − 4.
Xem thêm các lời giải bài tập Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 1 trang 34 Toán 11 Tập 2: Rút gọn biểu thức 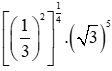
Bài 2 trang 34 Toán 11 Tập 2: Nếu 2α = 9 thì có giá trị bằng...
Bài 3 trang 34 Toán 11 Tập 2: Nếu thì...
Bài 4 trang 34 Toán 11 Tập 2: Nếu thì 3x có giá trị bằng...
Bài 5 trang 34 Toán 11 Tập 2: Cho α, β là hai số thực với α < β. Khẳng định nào sau đây đúng?...
Bài 6 trang 34 Toán 11 Tập 2: Hình nào vẽ đồ thị của hàm số ?...
Bài 7 trang 34 Toán 11 Tập 2: Phương trình có nghiệm là...
Bài 8 trang 34 Toán 11 Tập 2: Tập nghiệm của bất phương trình 0,53x1>0,25 là...
Bài 9 trang 34 Toán 11 Tập 2: Nếu thì...
Bài 10 trang 34 Toán 11 Tập 2: Số nguyên dương nhỏ nhất thỏa mãn là...
Bài 11 trang 35 Toán 11 Tập 2: Biết 4α + 4−α = 5. Tính giá trị biểu thức...
Bài 12 trang 35 Toán 11 Tập 2: Tính giá trị của biểu thức...
Bài 14 trang 35 Toán 11 Tập 2: Viết công thức biểu thị y theo x, biết...
Bài 15 trang 35 Toán 11 Tập 2: Giải các phương trình sau:...
Bài 16 trang 35 Toán 11 Tập 2: Giải các bất phương trình...
Xem thêm các bài giải SGK Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác: