Tailieumoi.vn xin giới thiệu Trắc nghiệm Toán lớp 8 Bài 4: Hình bình hành sách Cánh diều. Bài viết gồm 25 câu hỏi trắc nghiệm với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài trắc nghiệm Toán 8.
Trắc nghiệm Toán 8 Bài 4: Hình bình hành
Câu 1 : Điền cụm từ thích hợp vào chỗ trống: “Tứ giác có hai đường chéo … thì tứ giác đó là hình bình hành”.
Đáp án : C
Câu 2 : Cho hình bình hành ABCD có , các góc còn lại của hình bình hành là:
Đáp án : A
Nên
Hình bình hành có các góc đối bằng nhau
Câu 3 : Cho hình bình hành ABCD. Qua giao điểm O của các đường chéo, vẽ một đường thẳng cắt các cạnh đối BC và AD theo thứ tự E và F (đường thẳng này không đi qua trung điểm của BC và AD). Chọn các khẳng định đúng:
Đáp án : A
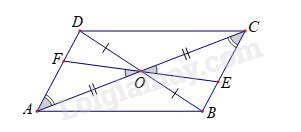
(g – c – g) suy ra AF = CE
Câu 4 : Cho hình bình hành ABCD. Gọi H, K lần lượt là hình chiếu của A, C trên đường thẳng BD. Chọn khẳng định đúng:
Đáp án : D
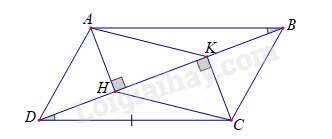
Xét tam giác AHB và CKD có: ; AB = CD;
Lại có:
Từ (1), (2) suy ra AHCK là hình bình hành.
Câu 5 : Chu vi của hình bình hành ABCD bằng 10 cm, chu vi của tam giác ABD bằng
9 cm. Khi đó độ dài BD là:
Đáp án : A
Vì chu vi của hình bình hành ABCD bằng 10 cm nên:
AB + BC + CD + DA = 10
Chu vi của tam giác ABD bằng 9 cm nên:
Câu 6 : Hãy chọn câu trả lời đúng
Đáp án : D
Dấu hiệu nhận biết: Tứ giác có các cạnh đối song song là hình bình hành.
Câu 7: Hãy chọn câu trả lời “sai”
Đáp án : B
Dấu hiệu nhận biết:
+ Tứ giác có các cạnh đối song song là hình bình hành nên A đúng.
+ Tứ giác có các cạnh đối bằng nhau là hình bình hành nên C đúng.
+ Tứ giác có các góc đối bằng nhau là hình bình hành nên D đúng.
Câu 8 : Hãy chọn câu trả lời “sai”
Đáp án : C
Dấu hiệu nhận biết:
+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành nên A, B đúng.
+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành nên D đúng.
Câu 9 : Hình bình hành ABCD thỏa mãn:
Đáp án : B
Câu 10 : Hãy chọn câu trả lời đúng
Đáp án : D
Trong hình bình hành hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Câu 11 : Hãy chọn câu đúng. Cho hình bình hành ABCD có các điều kiện như hình vẽ, trong hình có:
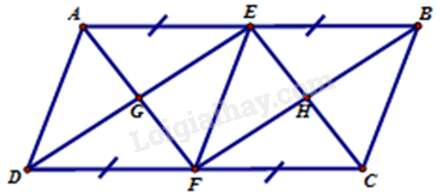
Đáp án : A

+ Vì ABCD là hình bình hành nên AB // CD, AD // BC
+ Xét tam giác AEFD có AE = FD; AE // FD (do AB // CD) nên AEFD là hình bình hành.
+ Xét tứ giác BEFC có BE = FC; BE // FC (do AB // CD) nên BEFC là hình bình hành
+ Xét tứ giác AECF có AE = FC; AE // FC (do AB // CD) nên AEFC là hình bình hành
+ Xét tứ giác BEDF có BE = FD, BE //FD (do AB // CD) nên BEDF là hình bình hành
+ Vì AECF là hình bình hành nên AF // EC ⇒ EH // GF; vì BEDF là hình bình hành nên ED // BF ⇒ EG // HF
Suy ra EGHF là hình bình hành
Vậy có tất cả 6 hình bình hành: ABCD; AEFD; BEFC; AECF; BEDF; EGHF
Câu 12 : Hãy chọn câu đúng. Cho hình bình hành ABCD, gọi E là trung điểm của AB, F là trung điểm của CD. Khi đó:
Đáp án : A
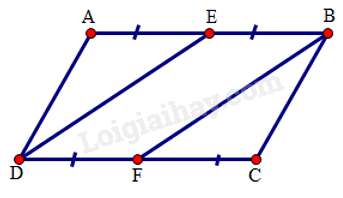
Vì ABCD là hình bình hành nên AB // CD; AB = CD
+ Xét tứ giác BEDF có BE =FD; BE // FD (do AB // CD) nên BFDE là hình bình hành.
Từ đó: DE = BF (tính chất hình bình hành)
Câu 13 : Hai góc kề nhau của một hình bình hành không thể có số đo là:
Đáp án : B
Trong hình bình hành có các góc đối nhau và tổng các góc trong hình bình hành phải bằng 3600 nên ta có:
600.2 + 1200.2 = 3600
400.2 + 500.2 = 1800 ≠ 3600
1300.2 + 500.2 = 3600
1050.2 + 750.2 = 3600
Do đó hai góc kề của hình bình hành không thể có số đo 400; 500
Câu 14 : Cho tam giác ABC và H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D. Chọn câu trả lời đúng nhất. Tứ giác BDCH là hình gì?
Đáp án : B
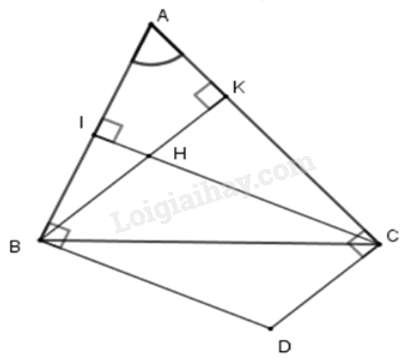
Gọi BK, CI là các đường cao của tam giác ABC. Khi đó BK ⊥ AC; CI ⊥ AB hay BH ⊥ AC; CH ⊥ AB (vì H là trực tâm).
Lại có BD ⊥ AB; CD ⊥ AC (giả thiết) nên BD // CH (cùng vuông với AB) và CD // BH (cùng vuông với AC)
Suy ra tứ giác BHCD là hình bình hành
Câu 15 : Cho tam giác ABC và H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D. Chọn câu sai.
Đáp án : D
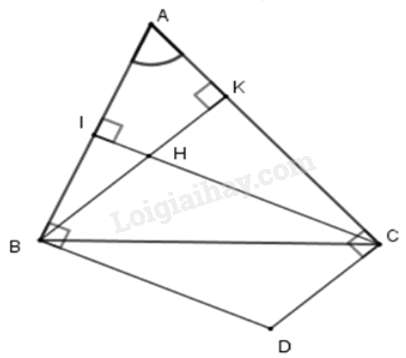
Gọi BK, CI là các đường cao của tam giác ABC. Khi đó BK ⊥ AC; CI ⊥ AB hay BH ⊥ AC; CH ⊥ AB (vì H là trực tâm).
Lại có BD ⊥ AB; CD ⊥ AC (giả thiết) nên BD // CH (cùng vuông với AB) và CD // BH (cùng vuông với AC)
Suy ra tứ giác BHCD là hình bình hành (dhnb)
Từ đó HB = CD; CH = BD nên D sai (ta chưa đủ điều kiện để chỉ ra được HB = HC)
Câu 16 : Cho tứ giác ABCD. Gọi E, F lần lượt là giao điểm của AB và CD, AD và BC; M, N, P, Q lần lượt là các điểm sao cho MN // AC; ; PQ // AC; . Khi đó MNPQ là hình gì? Chọn đáp án đúng nhất.
Đáp án : A

Nối AC.
Xét tam giác EAC suy ra MN // AC; (1)
Xét tam giác FAC suy ra PQ // AC; (2)
Từ (1) và (2) suy ra PQ // NM; PQ = MN nên MNPQ là hình bình hành.
Câu 17 : Tỉ số độ dài hai cạnh của hình bình hành là 3 : 5. Còn chu vi của nó bằng 48cm. Độ dài cạnh kề của hình bình hành là:
Đáp án : D
Gọi độ dài hai cạnh của hình bình hành là a và b với a, b > 0
Theo bài ra ta có:
Nửa chu của hình bình hành là: 48 : 2 = 24cm
Suy ra: a + b = 24cm. Theo tính chất của dãy tỉ số bằng nhau ta có:
⇒ a = 3.3 = 9; b = 3.5 = 15
Vậy hai cạnh của hình bình hành là 9cm và 15cm
Câu 18 : Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm E và F sao cho . Chọn khẳng định đúng.
Đáp án : A
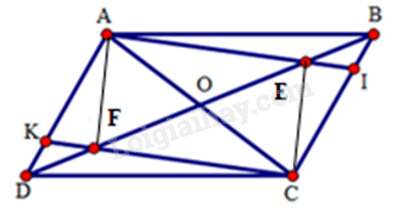
Gọi O là giao điểm của AC và BD. Ta có OA = OC, OB = OD
Mà BE = DF (gt) ⇒ OE = FO.
Tứ giác AECF có hai đường chéo AC và EF cắt nhau tại trung điểm O nên AECF là hình bình hành
⇒ FA = CE
Câu 19 : Cho tam giác ABC và H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D. Tính số đo góc BDC, biết .
Đáp án : D
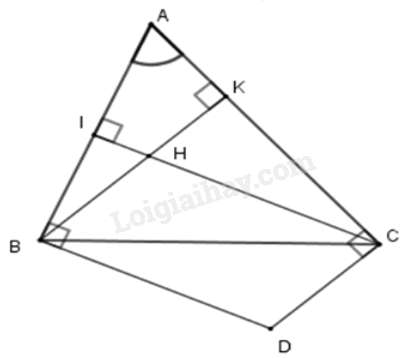
Xét tứ giác AIHK có:
(định lí tổng các góc trong của tứ giác)
Suy ra: (hai góc đối đỉnh)
Vì tứ giác BHCD là hình bình hành nên:
Vậy
Câu 20 : Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở E, F. Chọn khẳng định đúng.
Đáp án : B
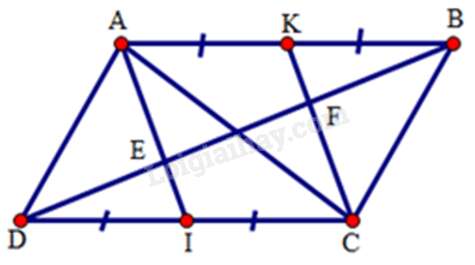
Vì (gt) mà AB = CD (cạnh đối hình bình hành) nên
AK = IC
Vì AB // CD (gt), K Є AB, I Є DC ⇒ AK // IC
Tứ giác AKCI có AK // IC, AK = IC (cmt) nên là hình bình hành. Suy ra AI // CK.
Mà E Є AI, F Є CK ⇒ EI // CF, KF // AE
Xét ΔDCF có: DI = IC (gt); IE // CF (cmt) ⇒ ED = FE (1)
Xét ΔABE có: AK = KB (gt), KF // AE (cmt) ⇒ EF = FB (2)
Từ (1) và (2) suy ra ED = FE = FB
Câu 21 : Cho tam giác ABC. Gọi D, M, E theo thứ tự là trung điểm của AB, BC, CA sao cho ME // AB; . Tứ giác ADME là:
Đáp án : B
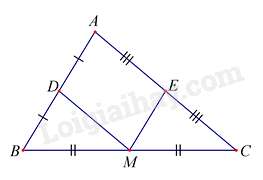
Vì
Vì và
Lại có: nên ADME là hình bình hành.
Câu 22 : Hình bình hành ABCD có . Số đo góc A bằng:
Đáp án : C
Ta có ABCD là hình bình hành nên mà
Câu 23 : Cho hình bình hành có . Số đo các góc của hình bình hành là:
Đáp án : D
Trong hình bình hành ABCD có các góc đối bằng nhau nên
Câu 24 : Cho tứ giác ABCD. Gọi E, F lần lượt là giao điểm của AB và CD; M, N, P, Q lần lượt là thuộc các cạnh AF, EC, BF, DE và ; . Khi đó MNPQ là hình gì? Chọn đáp án đúng nhất.
Đáp án : A

Nối EF; EP, FQ, EM, PM, QN. Gọi O là giao của QN và EF.
Xét tam giác CED ta có:
⇒ NFQE là hình bình hành nên hai đường chéo QN và EF giao nhau tại trung điểm của mỗi đường. Suy ra O là trung điểm của QN và EF (1)
Xét tam giác ABF ta có:
⇒ EMFB là hình bình hành nên hai đường chéo PM và EF giao nhau tại trung điểm của mỗi đường. Mà O là trung điểm của EF nên O cũng là trung điểm của PM (2)
Từ (1) và (2) suy ra: tứ giác QMNP có hai đường chéo QN, PM giao nhau tại trung điểm O mỗi đường nên QMNP là hình bình hành
Câu 25 : Cho hình bình hành ABCD. Gọi E, F theo thứ tự là trung điểm của AD, BC. Đường chéo AC cắt BE, DF theo thứ tự ở K, I. Chọn khẳng định đúng nhất.
Đáp án : C

Gọi O là giao điểm của AC, BD
Vì ABCD là hình bình hành nên AC, BD giao nhau tại trung điểm O mỗi đường, hay
Xét tam giác ABD có BE, AO là đường trung tuyến cắt nhau tại K nên K là trọng tâm ΔABD.
Suy ra (1)
Xét tam giác CBD có DF, CO là hai đường trung tuyến cắt nhau tại I nên I là trọng tâm ΔCBD.
Suy ra (2)
Lại có:
Từ (1), (2) và (3) suy ra: AK = KI = IC
Xem thêm các bài giải Trắc nghiệm Toán lớp 8 Cánh diều hay, chi tiết khác: