Với giải Bài 5 trang 94 Toán 11 Tập 2 Cánh diều chi tiết trong Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải bài tập Toán lớp 11 Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

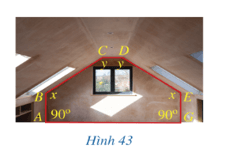
Bài 5 trang 94 Toán 11 Tập 2: Trong Hình 43, xét các góc nhị diện có góc phẳng nhị diện tương ứng là $\widehat{B},\widehat{\text{\hspace{0.17em}}C},\widehat{D},\widehat{E}$  trong cùng mặt phẳng. Lục giác ABCDEG nằm trong mặt phẳng đó có AB = GE = 2 m, BC = DE, $\widehat{A}=\widehat{G}=90°,$ $\widehat{B}=\widehat{E}=x,$$\widehat{C}=\widehat{D}=y.$ Biết rằng khoảng cách từ C và D đến AG là 4 m, AG = 12 m, CD = 1 m. Tìm x, y (làm tròn kết quả đến hàng đơn vị theo đơn vị độ).

Lời giải:

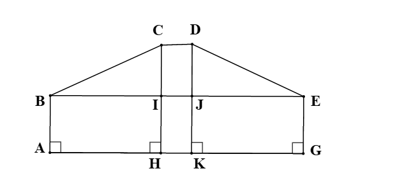
Kẻ CH ⊥ AG (H ∈ AG), DK ⊥ AG (K ∈ AG).

Gọi I = BE ∩ CH, J = BE ∩ DK.

Ta có $\widehat{A}=\widehat{G}=90°$ nên AB ⊥ AG và EG ⊥ AG.

Suy ra AB // EG.

⦁ Xét tứ giác ABEG có: AB // EG, AB = EG.

Suy ra ABEG là hình bình hành.

Hơn nữa $\widehat{A}=90°$ nên ABEG là hình chữ nhật.

Suy ra BE = AG = 12 m và BE // AG.

⦁ Xét tứ giác ABIH có:

BI // AH (do BE //AG);

AB // IK (do cùng vuông góc với AG)

Suy ra ABIH là hình bình hành.

Hơn nữa $\widehat{A}=90°$ nên ABIH là hình chữ nhật.

Suy ra IH = AB = 2 m và $\widehat{BIH}=90°.$

Tương tự ta dễ dàng có: JEGK và CDJI là hai hình chữ nhật.

Từ đó ta có: JK = EG = 2 m và $\widehat{EJK}=90°$(do JEGK là hình chữ nhật);

                     IJ = CD = 1 m và CD // IJ (do CDJI là hình chữ nhật).

Suy ra: CI = CH – IH = 4 – 2 = 2 m;

             DJ = DK – JK = 4 – 2 = 2 m.

⦁ Xét tam giác BCI và tam giác EDJ có:

$\widehat{BIC}=\widehat{CJD}=90°$ (do $\widehat{BIH}=\widehat{EJK}=90°);$

BC = ED (giả thiết);

CI = DJ (cùng bằng 2 m).

Do đó ∆BCI = ∆EDJ (cạnh huyền – cạnh góc vuông).

$\Rightarrow BI=EJ=\frac{BE-IJ}{2}=\frac{12-1}{2}=5,5m.$

Vì tam giác BCI vuông tại I nên ta có:

$\tan \widehat{IBC}=\frac{CI}{BI}=\frac{2}{5,5}=\frac{4}{11}\Rightarrow \widehat{IBC}\approx 20°.$

$\Rightarrow x=\widehat{ABI}+\widehat{IBC}\approx 90°+20°=110°.$

Ta cũng có $\widehat{BCI}=90°-\widehat{IBC}\approx 90°-20°=70°.$

Do đó $y=\widehat{BCD}=\widehat{BCI}+\widehat{ICD}\approx 70°+90°=160°.$

Vậy x ≈ 110° và y ≈ 160°.