Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 11 Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện chi tiết sách Toán 11 Tập 2 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 11. Mời các bạn đón xem:

Giải bài tập Toán lớp 11 Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

Giải Toán 11 trang 89 Tập 2

Câu hỏi khởi động trang 89 Toán 11 Tập 2: Hình 32 biểu diễn một chiếc gậy dựa vào tường. Bạn Hoa nói góc nghiêng giữa chiếc gậy và mặt đất bằng 65°.

Góc nghiêng giữa chiếc gậy và mặt đất được hiểu như thế nào?

Lời giải:

Góc nghiêng giữa chiếc gậy và mặt đất được hiểu là góc tạo bởi giữa chiếc gậy và đường thẳng hình chiếu của chiếc gậy đó xuống mặt đất.

I. Góc giữa đường thẳng và mặt phẳng

Hoạt động 1 trang 89 Toán 11 Tập 2: Quan sát Hình 32 và cho biết:

a) Hình chiếu của đường thẳng MO trên mặt phẳng (P) là đường thẳng nào;

b) Góc giữa đường thẳng MO và hình chiếu của đường thẳng đó trên mặt phẳng (P) là góc nào.

Lời giải:

a) Vì MH ⊥ (P) và O ∈ (P) nên hình chiếu của đường thẳng MO trên mặt phẳng (P) là đường thẳng HO.

b) Vì hình chiếu của đường thẳng MO trên mặt phẳng (P) là đường thẳng HO nên góc giữa đường thẳng MO và hình chiếu của đường thẳng đó trên mặt phẳng (P) là góc giữa hai đường thẳng MO và HO và là góc $\widehat{MOH}.$

Giải Toán 11 trang 90 Tập 2

Luyện tập 1 trang 90 Toán 11 Tập 2: Giả sử ở những giây đầu tiên sau khi cất cánh, máy bay chuyển động theo một đường thẳng tạo với mặt đất một góc 20° và có tốc độ 200 km/h. Tính độ cao của máy bay so với mặt đất theo đơn vị mét sau khi máy bay rời khỏi mặt đất 2 giây (làm tròn kết quả đến hàng phần mười).

Lời giải:

Đổi 200 km/h = $\frac{500}{9}$ m/s.

Bài toán được mô hình hóa như hình vẽ trên, với OA là quãng đường máy bay bay được sau 2 giây, AH là độ cao của máy bay so với mặt đất khi máy bay rời khỏi mặt đất sau 2 giây, góc $\widehat{AOH}$ là góc giữa đường thẳng được tạo thành khi máy bay cất cánh và mặt đất.

Sau 2 giây máy bay bay được quãng đường là $s=vt=\frac{500}{9}\cdot 2=\frac{1000}{9}$ (m).

Hay $OA=\frac{1000}{9}$ (m).

Xét tam giác OAH vuông tại H có: $\sin \widehat{AOH}=\frac{AH}{OA}$

Suy ra $AH=OA\cdot \sin \widehat{AOH}=\frac{1000}{9}\cdot \sin 20°\approx 38,0.$

Vậy độ cao của máy bay so với mặt đất sau khi máy bay rời khỏi mặt đất 2 giây là 38,0 m.

II. Góc nhị diện

Giải Toán 11 trang 91 Tập 2

Hoạt động 2 trang 91 Toán 11 Tập 2: Quan sát hình ảnh một quyển sổ được mở ra (Hình 35), mỗi trang sổ gợi nên hình ảnh của một nửa mặt phẳng. Nêu đặc điểm của hai nửa mặt phẳng đó.

Lời giải:

Mỗi trang sổ đều được gắn cố định và giới hạn bởi gáy sổ. Nên nếu mỗi trang sổ gợi nên hình ảnh của một nửa mặt phẳng thì hai nửa mặt phẳng đó có chung bờ là đường thẳng chứa gáy sổ.

Luyện tập 2 trang 91 Toán 11 Tập 2: Trong không gian cho hai mặt phẳng (α), (β) cắt nhau theo giao tuyến d. Hai mặt phẳng (α), (β) tạo nên bao nhiêu góc nhị diện có cạnh của góc nhị diện là đường thẳng d?

Lời giải:

Gọi M, N là hai điểm bất kì lần lượt thuộc hai mặt phẳng (α), (β).

Góc nhị diện được tạo bởi hai mặt phẳng (α), (β) có cạnh của góc nhị diện là đường thẳng d là [M, d, N].

Vì có vô số điểm M và N khác nhau thuộc hai mặt phẳng (α), (β) nên hai mặt phẳng (α), (β) tạo nên vô số góc nhị diện có cạnh của góc nhị diện là đường thẳng d.

Giải Toán 11 trang 92 Tập 2

Hoạt động 3 trang 92 Toán 11 Tập 2: Cho góc nhị diện có hai mặt là hai nửa mặt phẳng (P), (Q) và cạnh của góc nhị diện là đường thẳng d

Qua một điểm O trên đường thẳng d, ta kẻ hai tia Ox, Oy lần lượt thuộc hai nửa mặt phẳng (P), (Q) và cùng vuông góc với đường thẳng d. Góc xOy gọi là góc phẳng nhị diện của góc nhị diện đã cho (Hình 38).

Giả sử góc x’O’y’ cũng là góc phẳng nhị diện của góc nhị diện đã cho với O’ khác O (Hình 39).

Hãy so sánh số đo của hai góc xOy và x’O’y’.

Lời giải:

Xét (P) có: Ox ⊥ d và Ox’ ⊥ d nên Ox // O’x’.

Xét (Q) có: Oy ⊥ d và Oy’ ⊥ d nên Oy // O’y’.

Từ đó ta có: góc giữa đường thẳng Ox và Oy bằng góc giữa đường thẳng O’x’ và O’y’ hay số đo của hai góc xOy và x’O’y’ bằng nhau.

Giải Toán 11 trang 93 Tập 2

Luyện tập 3 trang 93 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA ⊥ (ABCD). Tính số đo của mỗi góc nhị diện sau:

a) [B, SA, D];

b) [B, SA, C].

Lời giải:

a) Ta có: SA ⊥ (ABCD) và AB ⊂ (ABCD), AD ⊂ (ABCD).

Suy ra: SA ⊥ AB, SA ⊥ AD.

Mà AB ∩ AD = A ∈ SA.

Do đó $\widehat{BAD}$ là góc phẳng nhị diện của góc nhị diện [B, SA, D].

Vì ABCD là hình vuông nên $\widehat{BAD}=90°.$

Vậy số đo của góc nhị diện [B, SA, D] bằng 90°.

b) Do SA ⊥ (ABCD) và AC ⊂ (ABCD) nên SA ⊥ AC.

Ta có: SA ⊥ AC, SA ⊥ AB (theo câu a) và AC ∩ AB = A ∈ SA.

Do đó $\widehat{BAC}$ là góc phẳng nhị diện của góc nhị diện [B, SA, C].

Vì ABCD là hình vuông nên đường chéo AC là đường phân giác của góc BAD, do đó $\widehat{BAC}=45°.$

Vậy số đo của góc nhị diện [B, SA, C] = 45°.

Bài tập

Giải Toán 11 trang 94 Tập 2

Bài 1 trang 94 Toán 11 Tập 2: Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hình thoi cạnh a và AC = a.

a) Tính số đo của góc nhị diện [B, SA, C].

b) Tính số đo của góc nhị diện [B, SA, D].

c) Biết SA = a, tính số đo của góc giữa đường thẳng SC và mặt phẳng (ABCD).

Lời giải:

a) Ta có: SA ⊥ (ABCD) và AB ⊂ (ABCD), AC ⊂ (ABCD).

Suy ra: SA ⊥ AB, SA ⊥ AC.

Mà AB ∩ AC = A ∈ SA.

Do đó $\widehat{BAC}$ là góc phẳng nhị diện của góc nhị diện [B, SA, C].

Vì ABCD là hinh thoi cạnh a và AC = a nên ta có AB = AC = BC = a.

Suy ra tam giác ABC đều. Khi đó $\widehat{BAC}=60°.$

Vậy số đo của góc nhị diện [B, SA, C] = 60°.

b) Ta có: SA ⊥ (ABCD) và AB ⊂ (ABCD), AD ⊂ (ABCD).

Suy ra: SA ⊥ AB, SA ⊥ AD.

Mà AB ∩ AD = A ∈ SA.

Do đó $\widehat{BAD}$ là góc phẳng nhị diện của góc nhị diện [B, SA, D].

Vì ABCD là hinh thoi cạnh a và AC = a nên ta có AD = AC = CD = a.

Suy ra tam giác ACD đều.

Khi đó $\widehat{CAD}=60°.$

Ta có: $\widehat{BAD}=\widehat{BAC}+\widehat{CAD}=60°+60°=120°.$

Vậy số đo của góc nhị diện [B, SA, D] bằng 120°.

c) Vì SA ⊥ (ABCD) nên AC là hình chiếu của SC trên (ABCD).

Suy ra góc giữa đường thẳng SA và mặt phẳng (ABC) là góc $\widehat{SCA}.$

Xét tam giác SAC vuông tại (do SA ⊥ AC theo câu a) có:

$\tan \widehat{SCA}=\frac{SA}{AC}=\frac{a}{a}=1.$ Do đó $\widehat{SCA}=45°.$

Vậy góc giữa đường thẳng SA và mặt phẳng (ABCD) bằng 45°.

Bài 2 trang 94 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, hai đường thẳng AC và BD cắt nhau tại O, SO ⊥ (ABCD), tam giác SAC là tam giác đều.

a) Tính số đo của góc giữa đường thẳng SA và mặt phẳng (ABCD).

b) Chứng minh rằng AC ⊥ (SBD). Tính số đo của góc giữa đường thẳng SA và mặt phẳng (SBD).

c) Gọi M là trung điểm của cạnh AB. Tính số đo của góc nhị diện [M, SO, D].

Lời giải:

a) Ta có SO ⊥ (ABCD) nên OA là hình chiếu của SA trên (ABCD).

Suy ra góc giữa đường thẳng SA và mặt phẳng (ABCD) bằng $\widehat{SAO}.$

Vì tam giác SAC là tam giác đều nên $\widehat{SAO}=60°.$

Vậy số đo của góc giữa đường thẳng SA và mặt phẳng (ABCD) bằng 60°.

b) Ta có: SO ⊥ (ABCD) và AC ⊂ (ABCD) nên SO ⊥ AC.

Vì ABCD là hình vuông nên AC ⊥ BD.

Ta có: AC ⊥ SO, AC ⊥ BD và SO ∩ BD = O trong (SBD).

Suy ra AC ⊥ (SBD).

Hay AO ⊥ (SBD) nên SO là hình chiếu của SA trên (SBD).

Suy ra góc giữa đường thẳng SA và mặt phẳng (SBD) bằng $\widehat{ASO}.$

Do ∆SAC đều nên đường cao SO đồng thời là đường phân giác của góc ASC.

Do đó $\widehat{ASO}=\frac{\widehat{ASC}}{2}=\frac{60°}{2}=30°.$

Vậy góc giữa đường thẳng SA và mặt phẳng (SBD) bằng 30°.

c) Ta có AC ∩ BD = O.

Vì O ∈ BD mà BD ⊂ (SBD) nên O ∈ (SBD).

Suy ra O = AC ∩ (SBD).

Mặt khác AC ⊥ (SBD).

Từ đó ta có O là hình chiếu của A trên (SBD).

Mà S ∈ (SBD) nên ta có SO là hình chiếu của SA trên (SBD).

Như vậy, góc giữa đường thẳng SA và mặt phẳng (SBD) bằng góc giữa hai đường thẳng SA và SO và bằng $\widehat{ASO}.$

Vì ABCD là hình vuông và AC ∩ BD = O nên O là trung điểm của AC và BD.

Xét tam giác SAC đều có SO là đường trung tuyến (do O là trung điểm của AC).

Suy ra SO cũng là đường phân giác của $\widehat{ASC}.$

Khi đó $\widehat{ASO}=\frac{\widehat{ASC}}{2}=\frac{60°}{2}=30°.$

Vậy số đo của góc giữa đường thẳng SA và mặt phẳng (SBD) bằng 30°.

c) Ta có: SO ⊥ (ABCD) và MO ⊂ (ABCD), DO ⊂ (ABCD).

Suy ra SO ⊥ MO, SO ⊥ DO.

Mà MO ∩ SO = O ∈ SO.

Như vậy, $\widehat{MOD}$ là góc phẳng nhị diện của góc nhị diện [M, SO, D].

Vì ABCD là hình vuông và O là giao điểm của AC và BD nên AC ⊥ BD tại O

Suy ra: $\widehat{AOD}=\widehat{AOB}=90°$ và OA = OB.

Như vậy tam giác OAB vuông cân tại O.

Mặt khác OM là đường trung tuyến trong tam giác OAB (do M là trung điểm của AB).

Suy ra OM là đường phân giác của $\widehat{AOB}.$

Do đó $\widehat{MOA}=\frac{\widehat{AOB}}{2}=\frac{90°}{2}=45°.$

Ta có: $\widehat{MOD}=\widehat{MOA}+\widehat{AOD}=45°+90°=135°.$

Vậy số đo của góc nhị diện [M, SO, D] bằng 135°.

Bài 3 trang 94 Toán 11 Tập 2: Dốc là đoạn đường thẳng nối hai khu vực hay hai vùng có độ cao khác nhau. Độ dốc được xác định bằng góc giữa dốc và mặt phẳng nằm ngang, ở đó độ dốc lớn nhất là 100%, tương ứng với góc 90° (độ dốc 10% tương ứng với góc 9°). Giả sử có hai điểm A, B nằm ở độ cao lần lượt là 200 m, 220 m so với mực nước biển và đoạn dốc AB dài 120 m. Độ dốc đó bằng bao nhiêu phần trăm (làm tròn kết quả đến hàng phần trăm)?

Lời giải:

Bài toán được mô hình hóa như bài vẽ trên, với:

⦁ AB là chiều dài con dốc;

⦁ BI là độ cao của con dốc so với mặt phẳng nằm ngang;

⦁ AH và BK lần lượt là độ cao của điểm A và điểm B so với mặt nước biển.

Theo bài ra ta có: AH =  200 m, BK = 220 m, AB = 120 m và độ dốc của con dốc là góc được tạo bởi đường thẳng AB và đường thẳng AI (do AI là hình chiếu của AB trên mặt phẳng nằm ngang) và chính là số đo của $\widehat{BAI}.$

Dễ thấy AHKI là hình chữ nhật nên IK = AH = 200 m.

Suy ra BI = BK – IK = 220 – 200 = 20 (m).

Vì tam giác ABI vuông tại I nên ta có:

$\sin \widehat{BAI}=\frac{BI}{AB}=\frac{20}{120}=\frac{1}{6}\Rightarrow \widehat{BAI}\approx 9,59°.$

Vì độ dốc 100% tương ứng với góc 90°.

Suy ra góc 9,59° có độ dốc là $\frac{9,59\cdot 100\%}{90}\approx 10,66\%.$

Vậy độ dốc của con dốc đó khoảng 10,66%.

Bài 4 trang 94 Toán 11 Tập 2: Trong Hình 42, máy tính xách tay đang mở gợi nên hình ảnh của một góc nhị diện. Ta gọi số đo góc nhị diện đó là độ mở của màn hình máy tính. Tính độ mở của màn hình máy tính đó, biết tam giác ABC có độ dài các cạnh là AB = AC = 30 cm và $BC=30\sqrt{3}$ cm.

Lời giải:

Gọi d là đường thẳng chứa bản lề của máy tính.

Suy ra d ⊥ AB, d ⊥ AC.

Mặt khác AB ∩ AC = A ∈ d.

Như vậy, $\widehat{BAC}$ là góc phẳng nhị diện của góc nhị diện [A, d, C].

Áp dụng hệ quả của định lí Cosin trong tam giác ABC ta có:

$\cos \widehat{BAC}=\frac{A{B}^2+A{C}^2-B{C}^2}{2\cdot AB\cdot AC}$

$\Rightarrow \cos \widehat{BAC}=\frac{{30}^2+{30}^2-{\left(30\sqrt{3}\right)}^2}{2\cdot 30\cdot 30}=-\frac{1}{2}.$

$\Rightarrow \widehat{BAC}=120°.$

Vậy độ mở của màn hình máy tính là 120°.

Bài 5 trang 94 Toán 11 Tập 2: Trong Hình 43, xét các góc nhị diện có góc phẳng nhị diện tương ứng là $\widehat{B},\widehat{\text{\hspace{0.17em}}C},\widehat{D},\widehat{E}$  trong cùng mặt phẳng. Lục giác ABCDEG nằm trong mặt phẳng đó có AB = GE = 2 m, BC = DE, $\widehat{A}=\widehat{G}=90°,$ $\widehat{B}=\widehat{E}=x,$$\widehat{C}=\widehat{D}=y.$ Biết rằng khoảng cách từ C và D đến AG là 4 m, AG = 12 m, CD = 1 m. Tìm x, y (làm tròn kết quả đến hàng đơn vị theo đơn vị độ).

Lời giải:

Kẻ CH ⊥ AG (H ∈ AG), DK ⊥ AG (K ∈ AG).

Gọi I = BE ∩ CH, J = BE ∩ DK.

Ta có $\widehat{A}=\widehat{G}=90°$ nên AB ⊥ AG và EG ⊥ AG.

Suy ra AB // EG.

⦁ Xét tứ giác ABEG có: AB // EG, AB = EG.

Suy ra ABEG là hình bình hành.

Hơn nữa $\widehat{A}=90°$ nên ABEG là hình chữ nhật.

Suy ra BE = AG = 12 m và BE // AG.

⦁ Xét tứ giác ABIH có:

BI // AH (do BE //AG);

AB // IK (do cùng vuông góc với AG)

Suy ra ABIH là hình bình hành.

Hơn nữa $\widehat{A}=90°$ nên ABIH là hình chữ nhật.

Suy ra IH = AB = 2 m và $\widehat{BIH}=90°.$

Tương tự ta dễ dàng có: JEGK và CDJI là hai hình chữ nhật.

Từ đó ta có: JK = EG = 2 m và $\widehat{EJK}=90°$(do JEGK là hình chữ nhật);

                     IJ = CD = 1 m và CD // IJ (do CDJI là hình chữ nhật).

Suy ra: CI = CH – IH = 4 – 2 = 2 m;

             DJ = DK – JK = 4 – 2 = 2 m.

⦁ Xét tam giác BCI và tam giác EDJ có:

$\widehat{BIC}=\widehat{CJD}=90°$ (do $\widehat{BIH}=\widehat{EJK}=90°);$

BC = ED (giả thiết);

CI = DJ (cùng bằng 2 m).

Do đó ∆BCI = ∆EDJ (cạnh huyền – cạnh góc vuông).

$\Rightarrow BI=EJ=\frac{BE-IJ}{2}=\frac{12-1}{2}=5,5m.$

Vì tam giác BCI vuông tại I nên ta có:

$\tan \widehat{IBC}=\frac{CI}{BI}=\frac{2}{5,5}=\frac{4}{11}\Rightarrow \widehat{IBC}\approx 20°.$

$\Rightarrow x=\widehat{ABI}+\widehat{IBC}\approx 90°+20°=110°.$

Ta cũng có $\widehat{BCI}=90°-\widehat{IBC}\approx 90°-20°=70°.$

Do đó $y=\widehat{BCD}=\widehat{BCI}+\widehat{ICD}\approx 70°+90°=160°.$

Vậy x ≈ 110° và y ≈ 160°.

Bài 6 trang 94 Toán 11 Tập 2: Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi α là số đo của góc nhị diện [A, BC, S]. Chứng minh rằng tỉ số diện tích của hai tam giác ABC và SBC bằng cosα.

Lời giải:

Kẻ AH ⊥ BC (H ∈ BC).

Vì SA ⊥ (ABC) và BC ⊂ (ABC) nên SA ⊥ BC.

Ta có: AH ⊥ BC, SA ⊥ BC và AH ∩ SA = A trong (SAH).

Suy ra BC ⊥ (SAH).

Mà SH ⊂ (SAH) nên BC ⊥ SH.

Ta có: AH ⊥ BC, SH ⊥ BC và AH ∩ SH = H ∈ BC.

Suy ra $\widehat{SHA}$ là góc phẳng nhị diện của góc nhị diện [A, BC, S], tức $\widehat{SHA}=\alpha .$

Vì SA ⊥ (ABC) và AH ⊂ (ABC) nên SA ⊥ AH.

Xét tam giác SAH vuông tại A (do SA ⊥ AH) có:

$\cos \alpha =\cos \widehat{SHA}=\frac{AH}{SH}.$

Diện tích tam giác ABC (có AH ⊥ BC) là: $S_{\Delta ABC}=\frac{1}{2}AH.BC.$

Diện tích tam giác SBC (có SH ⊥ BC) là: $S_{\Delta SBC}=\frac{1}{2}SH.BC.$

$\Rightarrow \frac{S_{\Delta ABC}}{S_{\Delta SBC}}=\frac{\frac{1}{2}AH.BC}{\frac{1}{2}SH.BC}=\frac{AH}{SH}=\cos \widehat{SHA}=\cos \alpha .$

Vậy tỉ số diện tích của hai tam giác ABC và SBC bằng cosα.

Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác:

Bài 2: Đường thẳng vuông góc với mặt phẳng

Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

Bài 4: Hai mặt phẳng vuông góc

Bài 5: Khoảng cách

Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối

Lý thuyết Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

1. Góc giữa đường thẳng và mặt phẳng

Cho đường thẳng d và mặt phẳng (P), ta có định nghĩa sau:

- Nếu đường thẳng d vuông góc với mặt phẳng (P) thì góc giữa d và (P) bằng ${90}^0$.

- Nếu đường thẳng d không vuông góc với mặt phẳng (P) thì góc giữa đường thẳng d và mặt phẳng (P) là góc giữa d và hình chiếu d’ của đường thẳng d trên (P).

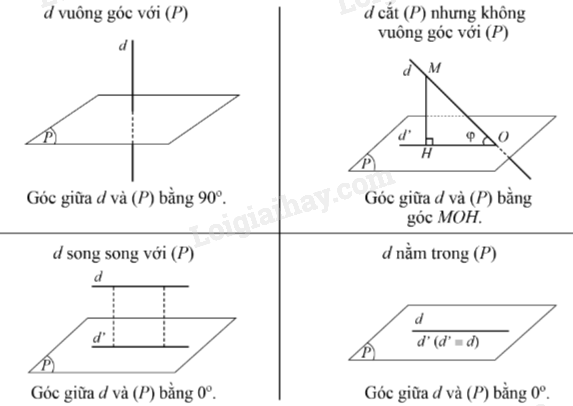
Nhận xét: Góc giữa đường thẳng và mặt phẳng có số đo từ $0^0$ đến ${90}^0$.

2. Góc nhị diện

a) Nửa mặt phẳng

Một đường thẳng nằm trong mặt phẳng chia mặt phẳng đó thành hai phần, mỗi phần được gọi là một nửa mặt phẳng và đường thẳng đó được gọi là bờ của một nửa mặt phẳng này.

b) Góc nhị diện

Góc nhị diện là hình gồm hai nửa mặt phẳng có chung bờ.

Ví dụ:  Xét góc nhị diện gồm hai nửa mặt phẳng (P) và (Q) có chung bờ là đường thẳng d, kí hiệu là [P, d, Q]. Đường thẳng d gọi là cạnh của góc nhị diện, mỗi nửa mặt phẳng (P) và (Q) gọi là một mặt của góc nhị diện.

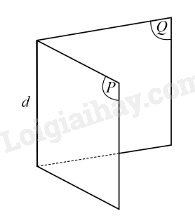
Chú ý: Góc nhị diện còn được kí hiệu là [M, d, N] với M, N lần lượt là các điểm thuộc các nửa mặt phẳng (P). (Q) nhưng không thuộc đường thẳng d.

c) Góc phẳng nhị diện

Trong không gian, cho góc nhị diện. Một góc có đỉnh thuộc cạnh của góc nhị diện, hai cạnh của góc đó lần lượt thuộc hai mặt nhị diện và cùng vuông góc với cạnh của góc nhị diện, được gọi là góc phẳng nhị diện của góc nhị diện đã cho.

Ví dụ: Cho góc nhị diện [P, d, Q]. Lấy O thuộc d, hai tia Ox, Oy lần lượt nằm trên hai nửa mặt phẳng (P), (Q) và cùng vuông góc với d. Khi đó góc xOy là góc phẳng nhị diện của góc nhị diện [P, d, Q].

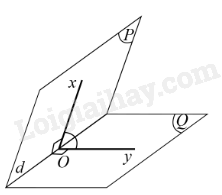
Nhận xét: Cạnh của góc nhị diện luôn vuông góc với mặt phẳng chứa góc phẳng nhị diện của góc nhị diện đó.

d) Số đo của góc nhị diện

- Số đo của một góc phẳng nhị diện được gọi là số đo của góc nhị diện đó.

- Nếu số đo góc phẳng nhị diện bằng 90° thì góc nhị diện đó gọi là góc nhị diện vuông.

Nhận xét: Số đo của góc nhị diện từ $0^0$ đến ${180}^0$.