Với giải Mở đầu trang 112 Toán 8 Tập 2 Kết nối tri thức chi tiết trong Bài 38: Hình chóp tam giác đều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:
Giải bài tập Toán lớp 8 Bài 38: Hình chóp tam giác đều
Mở đầu trang 112 Toán 8 Tập 2: Đỉnh FANSIPAN (Lào Cai) cao 3 143 m, là đỉnh núi cao nhất Đông Dương. Trên đỉnh núi, người ta đặt một chóp làm bằng inox có dạng hình chóp tam giác đều cạnh đáy dài 60 cm, cạnh bên dài khoảng 96,4 cm (H.10.1). Hỏi tổng diện tích các mặt bên của hình chóp là bao nhiêu?
Lời giải:
Sau bài học này, ta sẽ giải quyết được bài toán trên như sau:
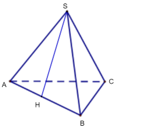
Giả sử hình chóp tam giác đều trên đỉnh núi là S.ABC. Khi đó tam giác ABC là tam giác đều có cạnh bằng 60 cm, các mặt bên SAB, SAC, SBC là các tam giác cân tại S với cạnh bên dài 96,4 cm.
Nửa chu vi của hình tam giác đều ABC là
p = (60 + 60 + 60) : 2 = 90 (cm).
Gọi SH là đường cao của tam giác SAB. Khi đó SH là trung đoạn của hình chóp tam giác đều.
Vì tam giác SAB cân tại S nên SH đồng thời là đường trung tuyến hay H chính là trung điểm của AB, suy ra HA = HB = (cm).
Tam giác SAH vuông tại H, theo định lý Pythagore, ta có:
SA2 = SH2 + HA2, suy ra SH2 = SA2 – HA2 = (96,4)2 – 302 = 8 392,96.
Do đó SH ≈ 91,61 cm.
Tổng diện tích các mặt bên của hình chóp hay diện tích xung quanh của hình chóp tam giác đều S.ABC là
Sxq ≈ 90 . 91,61 = 8 244,9 (cm2).
Xem thêm các lời giải bài tập Toán lớp 8 Kết nối tri thức hay, chi tiết khác:
Xem thêm các bài giải SGK Toán lớp 8 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
