Với lời giải SBT Toán 8 trang 30 Tập 1 Bài tập cuối chương 2 sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài tập cuối chương 2

• Bài 2.20 trang 30 sách bài tập Toán 8 Tập 1: Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến x.

  a) (x + 1)³ – (x – 1)³ – 6x²;

  b) (2x – 3)² + (2x + 3)² – 2(2x – 3)(2x + 3);

  c) (x – 3)(x² + 3x + 9) – (x + 2)(x² – 2x + 4).

  Lời giải:

  a) Cách 1:

  (x + 1)³ – (x – 1)³ – 6x²

  = x³ + 3x² + 3x + 1 ‒ (x³ ‒ 3x² + 3x ‒ 1) ‒ 6x²

  = x³ + 3x² + 3x + 1 ‒ x³ + 3x² ‒ 3x + 1 ‒ 6x²

  = (x³ ‒ x³) + (3x² + 3x² ‒ 6x²) + (3x ‒ 3x) + 1 + 1

  = 2.

  Vậy giá trị của biểu thức không phụ thuộc vào giá trị của biến x.

  Cách 2:

  (x + 1)³ – (x – 1)³ – 6x²

  = (x + 1 – x + 1)[(x + 1)² + (x + 1)(x – 1) + (x – 1)²] – 6x²

  = 2(x² + 2x + 1 + x² – 1 + x² – 2x + 1) – 6x²

  = 2(3x² + 1) – 6x²

  = 6x² + 2 – 6x²

  = 2.

  Vậy giá trị của biểu thức không phụ thuộc vào giá trị của biến x.

  b) Cách 1:

  (2x – 3)² + (2x + 3)² – 2(2x – 3)(2x + 3)

  = 4x² ‒ 12x + 9 + 4x² + 12x + 9 ‒ 2(4x² ‒ 9)

  = 4x² ‒ 12x + 9 + 4x² + 12x + 9 ‒ 8x² + 18

  = (4x² + 4x² ‒ 8x²) + (‒12x + 12x) + 9 + 18 = 36.

  Vậy giá trị của biểu thức không phụ thuộc vào giá trị của biến x.

  Cách 2:

  (2x – 3)² + (2x + 3)² – 2(2x – 3)(2x + 3)

  = (2x – 3)² – 2.(2x – 3).(2x + 3) + (2x + 3)²

  = [2x – 3 – (2x + 3)]²

  = (2x – 3 – 2x – 3)²

  = (–6)² = 36.

  Vậy giá trị của biểu thức không phụ thuộc vào giá trị của biến x.

  c) (x – 3)(x² + 3x + 9) – (x + 2)(x² – 2x + 4)

  = (x – 3)(x² + 3x + 3²) – (x + 2)(x² – 2x + 2²)

  = x³ ‒ 3³ ‒ (x³ + 2³)

  = x³ ‒ 27 ‒ x³ ‒ 8

  = (x³ ‒ x³) ‒ 27 ‒ 8 = ‒35.

  Vậy giá trị của biểu thức không phụ thuộc vào giá trị của biến x.

  Bài 2.21 trang 30 sách bài tập Toán 8 Tập 1: Không cần tính, hãy so sánh số A với số B trong các trường hợp sau:

  a) A = 2021 . 2023 và B = 2022²;

  b) A = 2021 . 2025 và B = 2023².

  Lời giải:

  a) Ta có A = 2021 . 2023

  = (2022 – 1).(2022 + 1)

  = 2022² – 1 < 2022².

  Vậy A < B.

  b) A = 2021 . 2025

  = (2023 – 2)(2023 + 2)

  = 2023² – 2 < 2023².

  Vậy A < B.

• Bài 2.22 trang 30 sách bài tập Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

  a) x³ – y³ + 2x – 2y;

  b) x² + 8xy + 16y² – 4z².

  Lời giải:

  a) x³ – y³ + 2x – 2y

  = (x³ – y³) + (2x – 2y)

  = (x − y)(x² + xy + y²) + 2(x – y)

  = (x − y)(x² + xy + y² + 2);

  b) x² + 8xy + 16y² – 4z²

  = (x² + 8xy + 16y²) – 4z²

  = (x + 4y)² – (2z)²

  = (x + 4y – 2z)(x + 4y + 2z).

  Bài 2.23 trang 30 sách bài tập Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

  a) x² – 3x + 2;

  b) x² + 7x + 6.

  Lời giải:

  a) x² – 3x + 2

  = x² ‒ 2x ‒ x + 2

  = (x² – 2x) – (x – 2)

  = x(x – 2) – (x – 2)

  = (x ‒ 2)(x ‒ 1).

  b) x² + 7x + 6

  = x² + x + 6x + 6

  = (x² + x) + (6x + 6)

  = x(x + 1) + 6(x + 1)

  = (x + 1)(x + 6).

• Bài 2.24 trang 30 sách bài tập Toán 8 Tập 1: Từ một miếng bìa có dạng hình tròn (H.2.4) với bán kính R (cm), người ta khoét một hình tròn ở giữa có bán kính r (cm), r < R.

  

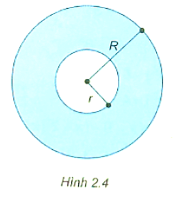
  a) Viết công thức tính diện tích phần còn lại của miếng bìa.

  b) Tính diện tích phần còn lại của miếng bìa biết tổng hai bán kính là 10 cm và hiệu hai bán kính là 3 cm.

  Lời giải:

  a) Diện tích miếng bìa hình tròn có bán kính R (cm) là: πR² (cm²)

  Diện tích miếng bìa hình tròn có bán kính r (cm) là: πr² (cm²)

  Diện tích phần còn lại của miếng bìa là:

  πR² ‒ πr² = π(R² – r²) (cm²).

  b) Ta có: π(R² – r²) = π(R – r)(R + r) (*)

  Do tổng hai bán kính là 10 cm và hiệu hai bán kính là 3 cm nên ta có:

  R + r = 10 và R ‒ r = 3

  Thay vào (*) ta được: π(10 − 3)(10 + 3) = π.7.13 = 91π.

  Vậy diện tích phần còn lại của miếng bìa là 91π (cm²).