Cho hình chóp S.ABCD có SA vuông góc (ABCD), biết ABCD là hình vuông cạnh bằng a

Van Anh Ngày: 10-11-2023 Lớp 11

359

Với giải Bài 7.52 trang 43 SBT Toán lớp 11 Kết nối tri thức chi tiết trong Bài tập cuối chương 7 trang 41giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:

Giải SBT Toán lớp 11 Bài tập cuối chương 7 trang 41

Bài 7.52 trang 43 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có SA $⊥$ (ABCD), biết ABCD là hình vuông cạnh bằng a và SA = a $\sqrt{2}$ .

a) Chứng minh rằng (SAC) $⊥$ (SBD) và (SAD) $⊥$ (SCD).

b) Gọi BE, DF là hai đường cao của tam giác SBD. Chứng minh rằng (ACF) $⊥$ (SBC) và (AEF) $⊥$ (SAC).

c) Tính theo a khoảng cách giữa hai đường thẳng BD và SC.

Lời giải:

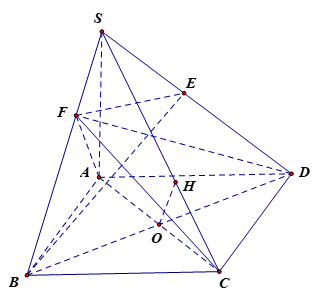
Cho hình chóp S.ABCD có SA vuông góc (ABCD), biết ABCD là hình vuông

a) Ta có ABCD là hình vuông nên AC $⊥$ BD. Mà SA $⊥$ (ABCD) nên SA $⊥$ BD.

Do đó BD $⊥$ (SAC) mà BD $\subset$ (SBD) nên (SAC) $⊥$ (SBD).

Vì ABCD là hình vuông nên AD $⊥$ CD mà SA $⊥$ (ABCD) nên CD $⊥$ SA.

Do đó CD $⊥$ (SAD) mà CD $\subset$ (SCD) nên (SAD) $⊥$ (SCD).

b) Vì ABCD là hình vuông nên AD $⊥$ AB mà SA $⊥$ (ABCD) nên AD $⊥$ SA.

Do đó AD $⊥$ (SAB), suy ra AD $⊥$ SB.

Vì DF là đường cao của tam giác SBD nên SB $⊥$ DF mà AD $⊥$ SB do đó SB $⊥$ (ADF), suy ra SB $⊥$ AF.

Vì ABCD là hình vuông nên AB $⊥$ BC, mà SA $⊥$ (ABCD) nên SA $⊥$ BC.

Do đó BC $⊥$ (SAB) nên BC $⊥$ AF.

Có SB $⊥$ AF và BC $⊥$ AF, do đó AF $⊥$ (SBC) mà AF $\subset$ (ACF) nên (ACF) $⊥$ (SBC).

Vì AF $⊥$ (SBC) nên AF $⊥$ SC.

Vì CD $⊥$ (SAD), suy ra CD $⊥$ AE.

Vì ABCD là hình vuông nên AD $⊥$ AB mà SA $⊥$ (ABCD) nên AB $⊥$ SA.

Vì AD $⊥$ AB và AB $⊥$ SA nên AB $⊥$ (SAD), suy ra AB $⊥$ SD.

Lại có BE là đường cao của tam giác SBD nên BE $⊥$ SD.

Vì AB $⊥$ SD và BE $⊥$ SD nên SD $⊥$ (ABE), suy ra SD $⊥$ AE.

Vì SD $⊥$ AE mà CD $⊥$ AE nên AE $⊥$ (SCD), suy ra AE $⊥$ SC mà AF $⊥$ SC.

Do đó SC $⊥$ (AEF) mà SC $\subset$ (SAC) nên (AEF) $⊥$ (SAC).

c) Gọi O là giao điểm của AC và BD, kẻ OH $⊥$ SC tại H.

Có AC $⊥$ BD và BD $⊥$ SA nên BD $⊥$ (SAC), suy ra OH $⊥$ BD.

Do đó OH là đoạn vuông góc chung của BD và SC hay d(BD, SC) = OH.

Xét tam giác ABC vuông tại B, có AC = $\sqrt{A B^{2} + B C^{2}} = \sqrt{a^{2} + a^{2}} = a \sqrt{2}$ .

Do ABCD là hình vuông nên O là trung điểm của AC nên OC = $\frac{A C}{2} = \frac{a \sqrt{2}}{2}$ .

Xét tam giác SAC vuông tại A nên SC = $\sqrt{S A^{2} + A C^{2}} = \sqrt{2 a^{2} + 2 a^{2}} = 2 a$

Xét $△$ CHO và $△$ CAS có góc C chung và $\hat{C H O} = \hat{C A S} = 90 °$ nên $△$ CHO đồng dạng với $△$ CAS, suy ra $\frac{O C}{C S} = \frac{O H}{A S}$ $\Rightarrow O H = \frac{O C \cdot A S}{C S}$ $= \frac{\frac{a \sqrt{2}}{2} \cdot a \sqrt{2}}{2 a}$ $= \frac{a}{2}$ .