Với lời giải Toán 11 trang 67 Tập 1 chi tiết trong Bài 9: Các số đặc trưng đo xu thế trung tâm sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải Toán 11 Bài 9: Các số đặc trưng đo xu thế trung tâm
a) Ghép nhóm dãy số liệu trên thành các khoảng có độ rộng bằng nhau, khoảng đầu tiên là [0; 5). Tìm giá trị đại diện cho mỗi nhóm.
b) Tính số trung bình của mẫu số liệu không ghép nhóm và mẫu số liệu ghép nhóm. Giá trị nào chính xác hơn?
c) Xác định nhóm chứa mốt của mẫu số liệu ghép nhóm thu được.
Lời giải:
a) Giá trị nhỏ nhất của mẫu số liệu là 2, giá trị lớn nhất của mẫu số liệu là 32, do đó khoảng biến thiên là 32 – 2 = 30.
Các nhóm có độ rộng bằng nhau và độ rộng của mỗi nhóm là 5. Để cho thuận tiện, ta chia thành 7 nhóm là các nhóm [0; 5), [5; 10), [10; 15), [15; 20), [20; 25), [25; 30), [30; 35). Đếm số giá trị thuộc mỗi nhóm, ta có mẫu số liệu ghép nhóm như sau:
|
Quãng đường (km) |
[0; 5) |
[5; 10) |
[10; 15) |
[15; 20) |
[20; 25) |
[25; 30) |
[30; 35) |
|
Số công nhân |
5 |
11 |
11 |
9 |
1 |
1 |
2 |
Giá trị đại diện cho mỗi nhóm là trung bình của hai đầu mút của nhóm. Ta có bảng giá trị đại diện như sau:
|
Quãng đường (km) (giá trị đại diện) |
2,5 |
7,5 |
12,5 |
17,5 |
22,5 |
27,5 |
32,5 |
|
Số công nhân |
5 |
11 |
11 |
9 |
1 |
1 |
2 |
b) Số trung bình của mẫu số liệu ghép nhóm là
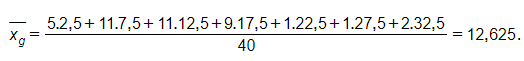
Ta có: 5 + 3 + 10 + 20 + 25 + 11 + 13 + 7 + 12 + 31 + 19 + 10 + 12 + 17 + 18 + 11 + 32 + 17 + 16 + 2 + 7 + 9 + 7 + 8 + 3 + 5 + 12 + 15 + 18 + 3 + 12 + 14 + 2 + 9 + 6 + 15 + 15 + 7 + 6 + 12 = 476.
Số trung bình của mẫu số liệu không ghép nhóm là .
Giá trị trung bình của mẫu số liệu không ghép nhóm chính xác hơn vì nó là giá trị của mẫu số liệu gốc.
c) Tần số lớn nhất trong bảng tần số của mẫu số liệu ghép nhóm là 11. Do đó, nhóm chứa mốt của mẫu số liệu ghép nhóm là các nhóm [5; 10) và [10; 15).
Bài 3.5 trang 67 Toán 11 Tập 1: Tuổi thọ (năm) của 50 bình ắc quy ô tô được cho như sau:
|
Tuổi thọ (năm) |
[2; 2,5) |
[2,5; 3) |
[3; 3,5) |
[3,5; 4) |
[4; 4,5) |
[4,5; 5) |
|
Tần số |
4 |
9 |
14 |
11 |
7 |
5 |
a) Xác định mốt và giải thích ý nghĩa.
b) Tính tuổi thọ trung bình của 50 bình ắc quy ô tô này.
Lời giải:
a) Tần số lớn nhất là 14 nên nhóm chứa mốt là nhóm [3; 3,5). Ta có, j = 3, a3 = 3, m3 = 14, m2 = 9, m4 = 11, h = 0,5. Do đó mốt của mẫu số liệu ghép nhóm là
.
Ý nghĩa: Tuổi thọ của bình ắc quy ô tô khoảng 3,3125 năm là nhiều nhất hay tuổi thọ chủ yếu của bình ắc quy ô tô khoảng 3,3125 năm.
b) Trong mỗi khoảng tuổi thọ, giá trị đại diện là trung bình cộng của giá trị hai đầu mút nên ta có bảng sau:
|
Tuổi thọ (năm) |
2,25 |
2,75 |
3,25 |
3,75 |
4,25 |
4,75 |
|
Tần số |
4 |
9 |
14 |
11 |
7 |
5 |
Tổng số ắc quy ô tô là 50. Tuổi thọ trung bình của 50 ắc quy ô tô này là
.
|
Điểm |
0 – 9 |
10 – 19 |
20 – 29 |
30 – 39 |
40 – 49 |
|
Số thí sinh |
1 |
2 |
4 |
6 |
15 |
|
Điểm |
50 – 59 |
60 – 69 |
70 – 79 |
80 – 89 |
90 – 99 |
|
Số thí sinh |
12 |
10 |
6 |
3 |
1 |
a) Hiệu chỉnh để thu được mẫu số liệu ghép nhóm dạng Bảng 3.2.
b) Tìm các tứ phân vị và giải thích ý nghĩa của chúng.
Lời giải:
a) Hiệu chỉnh để thu được mẫu số liệu ghép nhóm dạng Bảng 3.2 ta được mẫu số liệu ghép nhóm như sau:
|
Điểm |
[0; 9,5) |
[9,5; 19,5) |
[19,5; 29,5) |
[29,5; 39,5) |
[39,5; 49,5) |
|
Số thí sinh |
1 |
2 |
4 |
6 |
15 |
|
Điểm |
[49,5; 59,5) |
[59,5; 69,5) |
[69,5; 79,5) |
[79,5; 89,5) |
[89,5; 99,5) |
|
Số thí sinh |
12 |
10 |
6 |
3 |
1 |
b) Cỡ mẫu là n = 60.
Gọi x1, x2, ..., x60 là điểm thi môn Toán của 60 thí sinh và giả sử dãy này đã được sắp xếp theo thứ tự tăng dần. Khi đó, trung vị là . Do hai giá trị x30, x31 thuộc nhóm [49,5; 59,5) nên nhóm này chứa trung vị. Do đó, p = 6; a6 = 49,5; m6 = 12; m1 + m2 + m3 + m4 + m5 = 1 + 2 + 4 + 6 + 15 = 28; a7 – a6 = 59,5 – 49,5 = 10 và ta có
.
Tứ phân vị thứ nhất Q1 là . Do x15 và x16 đều thuộc nhóm [39,5; 49,5) nên nhóm này chứa Q1. Do đó, p = 5; a5 = 39,5; m5 = 15; m1 + m2 + m3 + m4 = 13; a6 – a5 = 10 và ta có
.
Tứ phân vị thứ ba Q3 là . Do x45 và x46 đều thuộc nhóm [59,5; 69,5) nên nhóm này chứa Q3. Do đó, p = 7; a7 = 59,5; m7 = 10; m1 + m2 + m3 + m4 + m5 + m6 = 40; a6 – a5 = 10 và ta có
.
Tứ phân vị thứ hai Q2 = Me ≈ 51,17.
Vậy các tứ phân vị của mẫu số liệu là Q1 ≈ 40,83; Q2 ≈ 51,17 và Q3 = 64,5. Các giá trị này các là ngưỡng để phân điểm của 60 học sinh thành 4 phần để xếp loại học sinh.
|
Thời gian |
Số học sinh nam |
Số học sinh nữ |
|
[4; 5) |
6 |
4 |
|
[5; 6) |
10 |
8 |
|
[6; 7) |
13 |
10 |
|
[7; 8) |
9 |
11 |
|
[8; 9) |
7 |
8 |
a) So sánh thời gian ngủ trung bình của các bạn học sinh nam và nữ.
b) Hãy cho biết 75% học sinh khối 11 ngủ ít nhất bao nhiêu giờ?
Lời giải:
a) Trong mỗi khoảng thời gian, giá trị đại diện là trung bình cộng của giá trị hai đầu mút nên ta có bảng sau:
|
Thời gian |
Số học sinh nam |
Số học sinh nữ |
|
4,5 |
6 |
4 |
|
5,5 |
10 |
8 |
|
6,5 |
13 |
10 |
|
7,5 |
9 |
11 |
|
8,5 |
7 |
8 |
Tổng số các bạn nam là n1 = 6 + 10 + 13 + 9 + 7 = 45.
Thời gian ngủ trung bình của các bạn học sinh nam là
.
Tổng số các bạn nữ là n2 = 4 + 8 + 10 + 11 + 8 = 41.
Thời gian ngủ trung bình của các bạn học sinh nữ là
.
Vì 6,52 < 6,77 nên thời gian ngủ trung bình của các học sinh nam ít hơn các học sinh nữ.
b) Ta có:
|
Thời gian |
Số học sinh nam |
Số học sinh nữ |
Số học sinh khối 11 |
|
[4; 5) |
6 |
4 |
10 |
|
[5; 6) |
10 |
8 |
18 |
|
[6; 7) |
13 |
10 |
23 |
|
[7; 8) |
9 |
11 |
20 |
|
[8; 9) |
7 |
8 |
15 |
Tổng số học sinh khối 11 được khảo sát là n = 45 + 41 = 86.
Gọi x1, x2, x3, ..., x86 là thời gian ngủ của các học sinh khối 11 được khảo sát và giả sử dãy này đã sắp xếp theo thứ tự tăng dần. Khi đó trung vị của mẫu số liệu là .
Do đó, tứ phân vị thứ ba Q3 = x65. Vì x65 thuộc nhóm [7; 8) nên nhóm này chứa Q3. Do đó, p = 4; a4 = 7; m4 = 20; m1 + m2 + m3 = 10 + 18 + 23 = 51; a5 – a4 = 8 – 7 = 1 và ta có
.
Tứ phân vị thứ ba Q3 chia mẫu số liệu thành 2 phần, phần dưới chiếm 75% số liệu của mẫu và phần trên chiếm 25% số liệu của mẫu.
Vậy 75% học sinh khối 11 ngủ ít nhất 7,675 giờ.
Video bài giảng Toán 11 Bài 9: Các số đặc trưng đo xu thế trung tâm - Kết nối tri thức
Xem thêm các lời giải bài tập Toán lớp 11 Kết nối tri thức hay, chi tiết khác:
HĐ1 trang 62 Toán 11 Tập 1: Khảo sát thời gian tự học của các học sinh trong lớp theo mẫu bên....
HĐ2 trang 63 Toán 11 Tập 1: Cho mẫu số liệu ghép nhóm về chiều cao của 21 câu na giống....
HĐ4 trang 66 Toán 11 Tập 1: Với số liệu cho trong Luyện tập 1:....
Bài 3.5 trang 67 Toán 11 Tập 1: Tuổi thọ (năm) của 50 bình ắc quy ô tô được cho như sau:...
Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác:
Bài 9: Các số đặc trưng đo xu thế trung tâm