Tailieumoi.vn xin giới thiệu tài liệu Trắc nghiệm Toán lớp 6 Chương 2: Số nguyên sách Cánh diều. Tài liệu gồm 33 câu hỏi trắc nghiệm chọn lọc có đáp án với đầy đủ các mức độ nhận biết, thông hiểu, vận dụng. Mời các bạn đón xem:
Trắc nghiệm Toán lớp 6 Chương 2: Số nguyên
Câu 1: Kết quả của phép tính (– 100) + (– 50) là:
A. – 50
B. 50
C. 150
D. – 150
Lời giải
Ta có: (– 100) + (– 50) = – (100 + 50) = – 150
Chọn đáp án D.
Câu 2: Tổng của hai số – 313 và – 211 là:
A. 534.
B. 524
C. – 524
D. – 534
Lời giải
Tổng của hai số – 313 và – 211 là: (– 313) + (– 211) = – (313 + 211) = – 524.
Chọn đáp án C.
Câu 3: Số nguyên nào dưới dây là kết quả của phép tính 52 + (– 122)?
A. – 70
B. 70
C. 60
D. – 60
Lời giải
Ta có: 52 + (– 122) = – (122 – 52) = – 70
Chọn đáp án A.
Câu 4: Chọn đáp án đúng?
A. (– 10) + (– 5) < – 16
B. 3 + 5 < – 3
C. (– 8) + (– 7) = (– 7) + (– 8)
D. (– 102) + (– 5) > – 100
Lời giải
Ta có:
(– 10) + (– 5) = – (10 + 5) = – 15 > – 16 . Đáp án A sai
3 + 5 = 8 > – 3 . Đáp án B sai
(– 8) + (– 7) = (– 7) + (– 8) (tính chất giao hoán của phép cộng). Đáp án C đúng
(– 102) + (– 5) = – (102 + 5) = – 107 < – 100. Đáp án D sai
Chọn đáp án C.
Câu 5: Nhiệt độ hiện tại của phòng đông lạnh là – 2°C . Nếu nhiệt độ giảm 7°C , nhiệt độ tại phòng đông lạnh sẽ là bao nhiêu?
A. 5°C
B. – 9°C
C. – 5°C
D. 9°C
Lời giải
Nhiệt độ giảm 7°C nghĩa là tăng – 7°C nên nhiệt độ tại phòng đông lạnh là:
(– 2) + (– 7) = – (2 + 7) = – 9°C
Chọn đáp án B.
Câu 6: Tính giá trị của biểu thức x + (– 16) , biết x = – 27:
A. – 43
B. – 11
C. 11
D. 43
Lời giải
Thay giá trị x = – 27 vào biểu thức đã cho, ta được:
x + (– 16) = – 27 + (– 16) = – (27 + 16) = – 43
Chọn đáp án A.
Câu 7: Cho các số: – 16; – 7; – 1; 0; 2; 7 . Hai trong các số trên có tổng bằng – 5 là:
A. – 7 + 2
B. – 7 + (– 1)
C. – 16 + 7
D. – 7 + 0
Lời giải
Ta có:
– 7 + 2 = – (7 – 2) = – 5
– 7 + (– 1) = – (7 + 1) = – 8
– 16 + 7 = – (16 – 7) = – 9
– 7 + 0 = – 7
Chọn đáp án A.
Câu 8: Tìm tổng tất cả các số nguyên x, biết: – 4 < x < 5 ?
A. 1
B. 5
C. 4
D. 3
Lời giải
Các số nguyên thỏa mãn – 4 < x < 5 là: – 3; – 2; – 1; 0; 1; 2; 3; 4.
Ta có:
(– 3) + (– 2) + (– 1) + 0 + 1 + 2 + 3 + 4
= (– 3 + 3) + (– 2 + 2) + (– 1 + 1) + 0 + 4
= 0 + 0 + 0 + 0 + 4 = 4
Chọn đáp án C.
Câu 9: Khoảng cách giữa hai điểm 5 và – 2 trên trục số là:
A. – 3
B. 3
C. – 7
D. 7
Lời giải
Khoảng cách giữa hai điểm 5 và – 2 trên trục số là:
5 – (– 2) = 5 + 2 = 7.
Chọn đáp án D.
Câu 10: Tính 125 – 200
A. – 75
B. 75
C. – 85
D. 85
Lời giải
Ta có: 125 – 200 = 125 + (– 200) = – (200 – 125) = – 75.
Chọn đáp án A.
Câu 11: Viết số sau: âm bốn trăm hai mươi ba.
A. 423
B. – 423
C. 234
D. + 423
Lời giải
Số âm bốn trăm hai mươi ba được viết là – 423.
Chọn đáp án B.
Câu 12: Cho các số: – 8; – 67; 0; 23; 58. Có bao nhiêu số nguyên âm trong các số đã cho?
A. 1
B. 2
C. 3
D. 4
Lời giải
Trong các số đã cho, có hai số là số nguyên âm, đó là – 8 và – 67.
Chọn đáp án B.
Câu 13: Số phần tử của tập hợp số nguyên âm là
A. 5 phần tử.
B. 10 phần tử.
C. 100 phần tử.
D. vô số phần tử.
Lời giải
Các số – 1, – 2, – 3, … là các số nguyên âm.
Do đó tập hợp các số nguyên âm có vô số phần tử.
Chọn đáp án D.
Câu 14: Nếu 20°C biểu diễn 20 độ trên 0°C thì – 5°C biểu diễn:
A. – 5°C trên 0°C
B. – 5°C dưới 0°C
C. 5°C trên 0°C
D. 5°C dưới 0°C
Lời giải:
Nếu 20°C biểu diễn 20 độ trên 0°C thì – 5°C biểu diễn 5°C dưới 0°C.
Chọn đáp án D.
Câu 15: Cho tập hợp A = {– 5; – 8; 0; 14; – 70; 65; – 450}.
Số phần tử là số nguyên âm có trong tập hợp A là:
A. 7
B. 6
C. 5
D. 4
Lời giải
Nhận thấy trong tập hợp A có các phần tử – 5; – 8; – 70; – 450 là các số nguyên âm. Do đó số phần tử là số nguyên âm có trong tập hợp A là 4 phần tử.
Chọn đáp án D.
Câu 16: Điền vào chỗ trống trong câu sau: Nếu – 2 điốp biểu diễn độ cận thị thì + 2 điốp biểu diễn …
A. độ cận thị
B. độ viễn thị
C. độ loạn thị
D. độ bình thường
Lời giải
Vì – 2 và + 2 là hai số đối nhau, mà – 2 điốp biểu thị độ cận thị thì + 2 điốp biểu diễn độ viễn thị
Chọn đáp án B.
Câu 17: Số đối của 8 là:
A. – 8
B. 0
C. 8
D. 16
Lời giải
Ta có số đối của 8 là – 8.
Chọn đáp án A.
Câu 18: Cho tập hợp A = {-2; 0; 3; 6} . Tập hợp B gồm các phần tử là số đối của các phần tử trong tập hợp A là:
A. B = {-2; 0; -3; -6}
B. B = {2; 0; 3; 6}
C. B = {-6; -3; 0; 2}
D. B = {-2; 0; 3; 6}
Lời giải
Ta có: số đối của – 2 là 2, số đối của 0 là 0, số đối của 3 là – 3 , số đối của 6 là – 6.
Do đó, tập hợp B là: B = {-6; -3; 0; 2}.
Chọn đáp án C.
Câu 19: Cho E = {− 4; 2; 0; − 1; 7; − 2020}. Viết tập hợp D gồm các phần tử thuộc E và là số nguyên âm.
A.D = {− 4; 2; − 1}
B.D = {−4 ; − 1; − 2020}
C.D = {− 1; 7; 2020}
D.D = {2; 0; 7}
Lời giải
Ta có E = {−4; 2; 0; −1; 7; −2020} có các số nguyên âm là − 4; − 1; − 2020. Nên tập hợp D = {− 4; − 1; − 2020}.
Chọn đáp án B.
Câu 20: Điểm - 3 cách điểm 4 theo chiều dương bao nhiêu đơn vị?
A. 7
B. 2
C. 9
D. 5
Lời giải
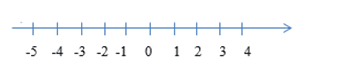
Quan sát trục số ta thấy điểm – 3 cách điểm 4 theo chiều dương là 7 khoảng hay chính là 7 đơn vị.
Chọn đáp án A.
Câu 21: Biểu diễn hiệu (– 28) – (–32) thành dạng tổng là:
A. (– 28) + (– 32)
B. (– 28) + 32
C. 28 + (– 32)
D. 28 + 32
Lời giải
Muốn trừ số nguyên a cho số nguyên b ta cộng a với số đối của b.
Ta có: số đối của – 32 là 32 nên: (– 28) – (–32) = – 28 + 32.
Chọn đáp án B.
Câu 22: Đơn giản biểu thức x + 1 982 + 172 + (– 1 982) – 162 ta được kết quả là:
A. x – 10
B. x + 10
C. 10
D. x
Lời giải
Ta có: x + 1 982 + 172 + (– 1 982) – 162
= x + [1 982 + (– 1 982)] + (172 – 162)
= x + 0 + 10
= x + 10
Chọn đáp án B.
Câu 23: Cho số nguyên b và b – x = – 9. Tìm x.
A. – 9 – b
B. – 9 + b
C. b + 9
D. – b + 9
Lời giải
Ta có: b – x = – 9
– x = – 9 – b
x = 9 + b
Vậy x = 9 + b = b + 9.
Chọn đáp án C.
Câu 24: Giá trị của x thỏa mãn – 15 + x = – 20
A. – 5
B. 5
C. – 35
D. 15
Lời giải
Ta có: – 15 + x = – 20
x = (– 20) – (– 15)
x = (– 20) + 15
x = – 5
Vậy x = – 5.
Chọn đáp án A.
Câu 25: Trong các khẳng định sau khẳng định đúng là:
A. Nếu a . b > 0 thì a và b là hai số nguyên dương
B. Nếu a . b > 0 thì a và b là hai số nguyên âm
C. Nếu a . b = 0 thì a = 0 và b = 0
D. Nếu a . b < 0 thì a và b là hai số nguyên khác dấu
Lời giải
Nếu a . b > 0 thì a và b là hai số nguyên cùng dấu, tức a và b có thể cùng là số nguyên âm hoặc cùng là số nguyên dương. Vậy đáp án A và B sai
Nếu a . b = 0 thì a = 0 hoặc b = 0. Vậy đáp án C sai.
Nếu a . b < 0 thì a và b là hai số nguyên khác dấu. Đáp án D đúng.
Chọn đáp án D.
Câu 26: Tích (– 4)2 . (– 2) bằng:
A. – 16
B. 16
C. – 32
D. 32
Lời giải
Ta có: (– 4)2 . (– 2) = 16 . (– 2) = – 32.
Chọn đáp án C.
Câu 27: Giá trị của biểu thức (x – 2)(x – 3) tại x = – 1 là:
A. – 12
B. 12
C. – 2
D. 2
Lời giải
Thay x = – 1 vào biểu thức ta được:
(x – 2)(x – 3) = (– 1 – 2)(– 1 – 3) = (– 3) . (– 4) = 3 . 4 = 12.
Vậy giá trị của biểu thức đã cho bằng 12 tại x = – 1.
Chọn đáp án B.
Câu 28: Giá trị của biểu thức (– 63) . (1 – 299) – 299 . 63 là:
A. – 63
B. 63
C. – 53
D. 53
Lời giải
Ta có: (– 63) . (1 – 299) – 299 . 63
= (– 63) . 1 + (– 63) . (– 299) – 299 . 63
= – 63 + 63 . 299 – 63 . 299 = – 63
Chọn đáp án A.
Câu 29: Tính tổng S = 1 – 3 + 5 – 7 + ... + 2001 – 2003.
A. S = – 1 000
B. S = – 1 001
C. S = – 1 002
D. S = – 1 003
Lời giải
Dãy số 1; 3; 5; 7; …; 2003 là dãy số cách đều nhau 2 đơn vị nên dãy này có số số hạng là: (2 003 – 1) . 2 + 1 = 2 002 : 2 + 1 = 1 001 + 1 = 1 002 (số hạng).
Khi ta nhóm các số lại với nhau thành cặp thì có tất cả: 1 002 : 2 = 501 (cặp số).
Ta có:
S = 1 – 3 + 5 – 7 + ... + 2001 – 2003
S = (1 – 3) + (5 – 7) + ... + (2001 – 2003)
S = (– 2) + (– 2) + ... + (– 2)
S = 501 . (– 2) = – 1 002
Chọn đáp án C.
Câu 30: Tính: (– 66) : (– 11) ta được kết quả là:
A. 6
B. 11
C. – 6
D. – 11
Lời giải
Ta có: (– 66) : (– 11) = 66 : 11 = 6.
Chọn đáp án A.
Câu 31: Kết quả của phép tính 65 : (– 13) là:
A. – 13
B. 13
C. 5
D. – 5
Lời giải
Ta có: 65 : (– 13) = – (65 : 13) = – 5.
Chọn đáp án D.
Câu 32: Tập hợp các ước của – 8 là:
A. A = {1; – 1; 2; – 2; 4; – 4; 8; – 8}
B. A = {0; ± 1; ± 2; ± 4; ± 8}
C. A = {1; 2; 4; 8}
D. A = {0; 1; 2; 4; 8}
Lời giải
Ta có – 8 = (– 1).8 = 1 . (– 8) = (– 2) . 4 = 2 . (– 4)
Tập hợp các ước của – 8 là A = {1; – 1; 2; – 2; 4; – 4; 8; – 8}.
Chọn đáp án A.
Câu 33: Viết tập hợp K các số nguyên x thỏa mãn (x + 3) ⁝ (x + 1).
A. K = {– 3; – 2; 0; 1}
B. K = {– 1; 0; 2; 3}
C. K = {– 3; 0; 1; 2}
D. K = {– 2; 0; 1; 3}
Lời giải
Ta có: x + 3 = (x + 1) + 2
Vì (x + 3) ⁝ (x + 1), (x + 1) ⁝ (x + 1) nên 2 ⁝ (x + 1)
Khi đó x + 1 là ước của 2.
Mà các ước của 2 là: – 1; 1; 2; – 2.
Do đó, x + 1 = ±1 hoặc x + 1 = ±2
Nếu x + 1 = 1 thì x = 0
Nếu x + 1 = – 1 thì x = – 2
Nếu x + 1 = 2 thì x = 1
Nếu x + 1 = – 2 thì x = – 3
Do đó các số nguyên x thỏa mãn yêu cầu là: – 3; – 2; 0; 1.
Vậy K = {– 3; – 2; 0; 1}.
Chọn đáp án A.
Xem thêm các bài trắc nghiệm Toán lớp 6 Cánh Diều hay, chi tiết khác:
Trắc nghiệm Chương 1: Số tự nhiên
Trắc nghiệm Chương 2: Số nguyên
Trắc nghiệm Chương 3: Hình học trực quan
Trắc nghiệm Chương 4: Một số yếu tố thống kê và xác suất
Trắc nghiệm Chương 5: Phân số và số thập phân
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
