Với lời giải SBT Toán 10 trang 65 Tập 1 chi tiết trong Bài 11: Tích vô hướng của hai vectơ sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:
Giải SBT Toán lớp 10 Bài 11: Tích vô hướng của hai vectơ
Bài 4.29 trang 65 SBT Toán 10 Tập 1:
Cho tam giác đều ABC có độ dài các cạnh bằng 1.
a) Gọi M là trung điểm của BC. Tính tích vô hướng của các cặp vectơ và , và
b) Gọi N là điểm đối xứng với B qua C. Tính tích vô hướng
c) Lấy điểm P thuộc đoạn AN sao cho AP = 3PN. Hãy biểu thị các vectơ theo hai vectơ và Tính độ dài đoạn MP.
Lời giải:
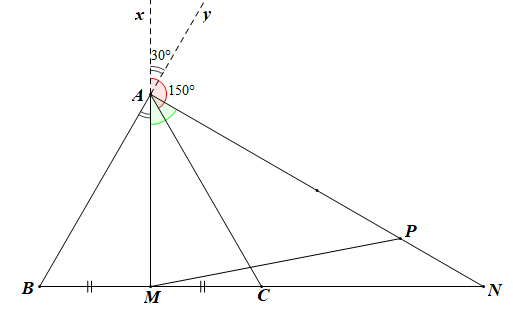
a) Tam giác ABC đều có M là trung điểm của BC nên đường trung tuyến AM đồng thời là đường phân giác và đường cao.
Gọi Ax là tia đối của tia AM, tia Ay là tia đối của tia AB.
Do đó
Khi đó ta có:
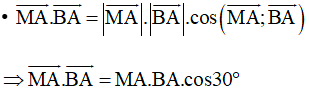
Xét tam giác BAM vuông tại M, theo định lí Pythagoras ta có:
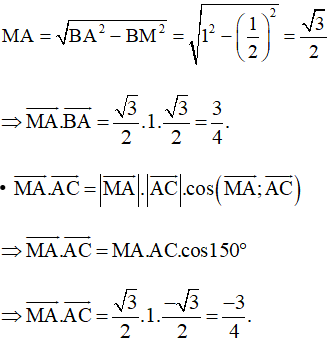
Vậy và
b) • Vì M là trung điểm của BC nên
• N đối xứng với B qua C nên C là trung điểm của BN
Khi đó
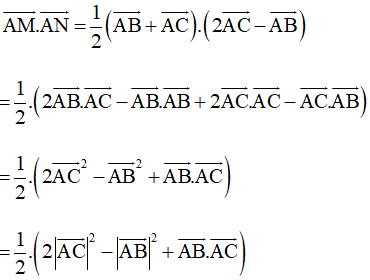
Mà
Do đó
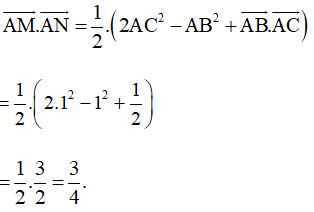
Vậy
c) • Vì P thuộc đoạn thẳng AN thỏa mãn AP = 3PN
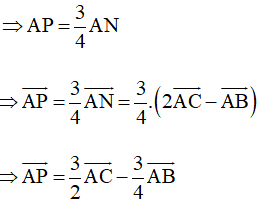
• Ta có:
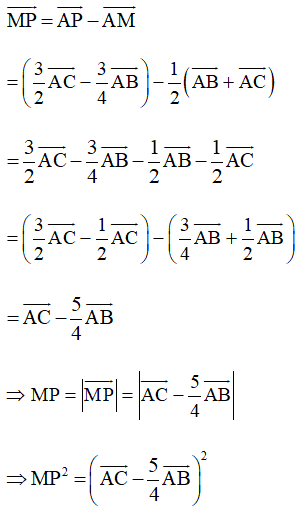
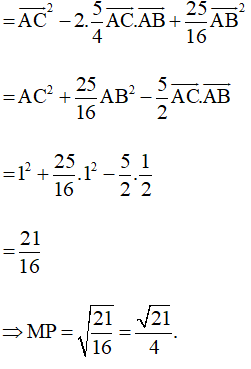
Vậy và
Bài 4.30 trang 65 SBT Toán 10 Tập 1:
Cho hình chữ nhật ABCD có AB = 1, Gọi M là trung điểm của AD.
a) Chứng minh rằng các đường thẳng AC và BM vuông góc với nhau.
b) Gọi H là giao điểm của AC, BM. Gọi N là trung điểm của AH và P là trung điểm của CD. Chứng minh rằng tam giác NBP là một tam giác vuông.
Lời giải:
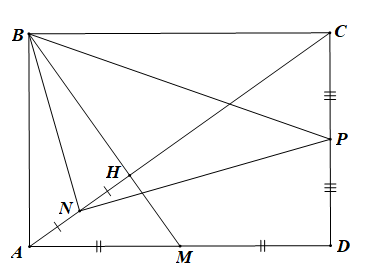
a) Đặt khi đó và
Vì AB ⊥ AD nên
ABCD là hình chữ nhật nên cũng là hình bình hành nên ta có:
(quy tắc hình bình hành)
M là trung điểm của AD nên
Suy ra
Khi đó
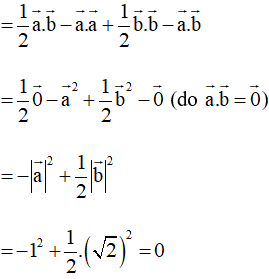
Do đó
Þ AC ⊥ BM.
b) • Xét tam giác ABC vuông tại C, theo định lí Pythagore ta có:
AC2 = AB2 + BC2 = 1 + = 3
Theo hệ thức lượng trong tam giác vuông ta có:
AB2 = AH.AC
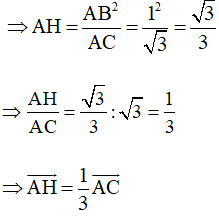
Khi đó và
Ta có (quy tắc ba điiểm)
Vì N là trung điểm của AH nên
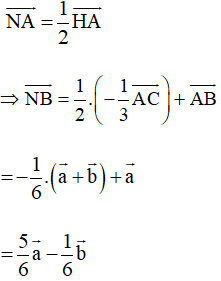
• Có N là trung điểm của HA và P là trung điểm của CD, theo kết quả bài 4.12, trang 58, Sách giáo khoa Toán 10, tập một, ta có:
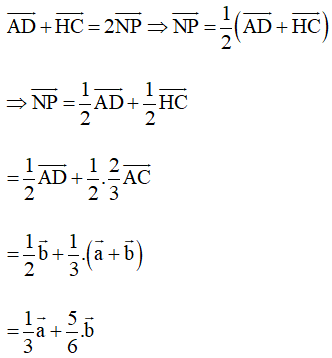
Khi đó
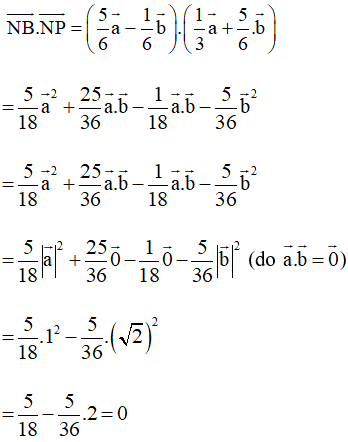
Do đó
Þ NB ⊥ NP.
Bài 4.31 trang 65 SBT Toán 10 Tập 1:
Cho tam giác ABC có Dựng ra phía ngoài tam giác hai tam giác vuông cân đỉnh A là ABD và ACE. Gọi M, N, P theo thứ tự là trung điểm BC, BD, CE. Chứng minh rằng:
a) AM vuông góc với DE;
b) BE vuông góc với CD;
c) Tam giác MNP là một tam giác vuông cân.
Lời giải:
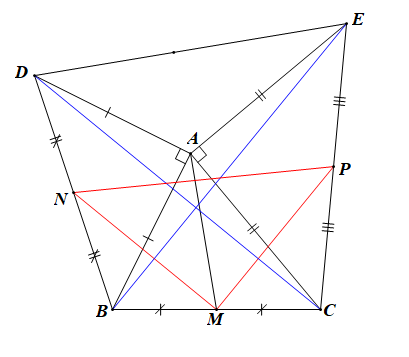
a) +) Vì M là trung điểm của BC nên
+) Theo quy tắc ba điểm ta có:
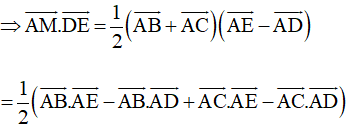
Mà AB ⊥ AD nên
Và AC ⊥ AE nên
Do đó
Ta có:
•
Và
• AB = AD (do ∆ABD vuông cân tại A)
Và AC = AE (do ∆ACE vuông cân tại A)
•
Và
Do đó
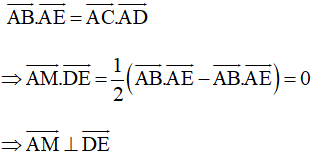
b) Ta có:
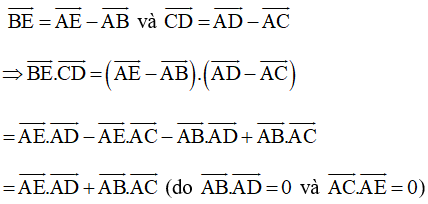
Ta có:
•
Và
• AB = AD và AC = AE
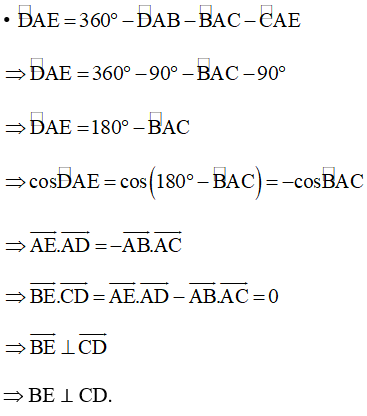
Þ BE ⊥ CD.
c) Ta có:
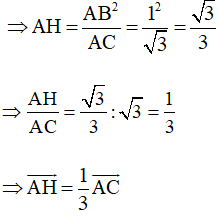
Þ BE = CD (1)
Xét tam giác BCD có M, N lần lượt là trung điểm của BC, BD
Nên MN là đường trung bình của ∆BCD
và MN // CD (2)
Chứng minh tương tự ta cũng có:
MP là đường trung bình của ∆BCE
và MP // BE (3)
Từ (1), (2) và (3) suy ra MN = MP.
Vì BE ⊥ CD (câu b), MN // CD và MP // BE
Nên MN ⊥ MP
Tam giác MNP có MN = MP và
Suy ra tam giác MNP là tam giác vuông cân tại M.
Bài 4.32 trang 65 SBT Toán 10 Tập 1:
Cho hai vectơ và thoả mãn và
a) Tính tích vô hướng
b) Tính số đo của góc giữa hai vectơ và
Lời giải:
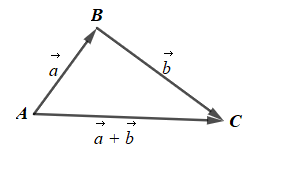
Gọi ba điểm A, B, C sao cho
Khi đó
Và AB = 6, BC = 8 và AC = 10.
Xét tam giác ABC có:
• AB2 + BC2 = 62 + 82 =100
AC2 = 102 = 100
Þ AB2 + BC2 = AC2
Do đó tam giác ABC vuông tại B (định lí Pythagore đảo)
•
a) Ta có
Vậy
b)
Vậy
Bài 4.33 trang 65 SBT Toán 10 Tập 1:
Cho tam giác ABC không cân. Gọi D, E, F theo thứ tự là chân các đường cao kẻ từ A, B, C; gọi M, N, P tương ứng là trung điềm các cạnh BC, CA, AB. Chứng minh rằng
Lời giải:
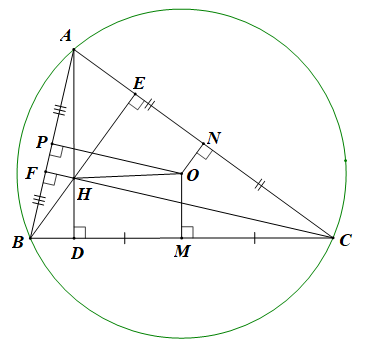
Gọi H và O là tâm đường tròn ngoại tiếp tam giác ABC.
• Vì D, M lần lượt là hình chiếu của H và O lên BC, nên là hình chiếu của trên giá của
Theo định lí hình chiếu (được giới thiệu ở phần Nhận xét của Ví dụ 2, trang 62, Sách Bài tập Toán 10, tập một) ta có:
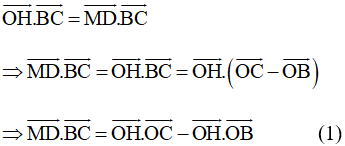
Chứng minh tương tự ta cũng có:
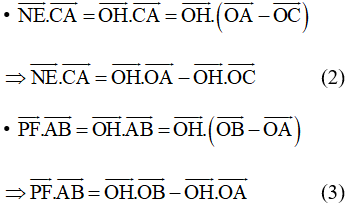
Từ (1), (2) và (3) ta có:
= 0
Vậy
Bài 4.34 trang 65 SBT Toán 10 Tập 1:
Trong mặt phẳng toạ độ Oxy cho hai điểm A(2; 1) và B(4; 3).
a) Tìm toạ độ của điểm C thuộc trục hoành sao cho tam giác ABC vuông tại A. Tính chu vi và diện tích của tam giác ABC.
b) Tìm toạ độ của điểm D sao cho tam giác ABD vuông cân tại A.
Lời giải:
a) Vì tam giác ABC vuông tại A nên AB ⊥ AC hay
Do đó
Giả sử C(x; 0) là điểm thuộc trục hoành.
Với A(2; 1), B(4; 3) và C(x; 0) ta có:
và
Khi đó Û 2(x – 2) + 2(–1) = 0
Û 2x – 4 – 2 = 0
Û 2x = 6
Û x = 3
Vậy C(3; 0).
Ta có:
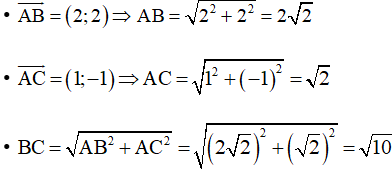
(theo định lí Pythagore)
Khi đó chu vi tam giác ABC là:
AB + AC + BC = (đơn vị độ dài)
Diện tích tam giác ABC là:
(đơn vị diện tích)
b) Tam giác ABD vuông cân tại A nên AB ⊥ AD và AB = AD
• Với AB ⊥ AD ta có
Mà (theo câu a)
Nên cùng phương với
Gọi D(a; b) là tọa độ điểm D cần tìm.
Mà
Do đó cùng phương với khi và chỉ khi:
Û a – 2 = 1 – b
Û b – 1 = 2 – a (4)
• Với AB = AD ta có AB2 = AD2
Û 8 = (a – 2)2 + (2 – a)2 (do b – 1 = 2 – a)
Û 8 = 2.(a – 2)2
Û (a – 2)2 = 4
Với a = 4 thì b – 1 = 2 – 4 Þ b = –1 ta có điểm D1(4; –1).
Với a = 0 thì b – 1 = 2 – 0 Þ b = 3 ta có điểm D2(0; 3).
Vậy có hai điểm D thỏa mãn yêu cầu đề bài là D1(4; –1) và D2(0; 3).
Bài 4.35 trang 65 SBT Toán 10 Tập 1:
Trong mặt phẳng toạ độ Oxy cho hai điểm A(1; 4) và C(9; 2) là hai đỉnh của hình vuông ABCD. Tìm toạ độ các đỉnh B, D, biết rằng tung độ của B là một số âm.
Lời giải:
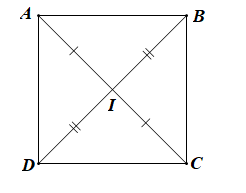
Gọi I là giao điểm của AC và BD
Vì ABCD là hình vuông nên ta có: I là trung điểm của AC; AC = BD và AC ⊥ BD tại I.
• I là trung điểm của AC nên:
Þ I(5; 3)
Giả sử B(x; y) (y < 0) và D(a; b)
Vì I là trung điểm của BD nên ta có:
Þ D(10 – x; 6 – y)
Với A(1; 4); C(9; 2); B(x; y) và D(10 – x; 6 – y) ta có:
và
• AC ⊥ BD
Û 8.(10 – 2x) + (–2).(6 – 2y) = 0
Û 80 – 16x – 12 + 4y = 0
Û 4y = 16x – 68
Û y = 4x – 17 (với y < 0)
• AC = BD Û AC2 = BD2
Û 82 + (–2)2 = (10 – 2x)2 + (6 – 2y)2
Û 64 + 4 = (10 – 2x)2 + [6 – 2(4x – 17)]2
Û (10 – 2x)2 + (6 – 8x + 34)2 = 68
Û (10 – 2x)2 + (40 – 8x)2 = 68
Û 4.(x – 5)2 + 64.(x – 5)2 = 68
Û (x – 5)2 = 1
Với x = 6 ta có y = 4.6 – 17 = 7 (không thỏa mãn y < 0)
Với x = 4 ta có y = 4.4 – 17 = –1 (thỏa mãn y < 0)
Khi đó ta có điểm B(4; –1)
Mà D(10 – x; 6 – y) nên D(6; 7).
Vậy B(4; –1) và D(6; 7).
Xem thêm các bài giải sách bài tập Toán 10 Kết nối tri thức hay, chi tiết khác:
Giải SBT Toán 10 trang 66 Tập 1
Xem thêm các bài giải SBT Toán 10 Kết nối tri thức hay, chi tiết khác:
Bài 10: Vectơ trong mặt phẳng tọa độ
Bài 11: Tích vô hướng của hai vectơ
Bài 13: Các số đặc trưng đo xu thế trung tâm