Với giải Bài 4.24 trang 63 SBT Toán lớp 11 Kết nối tri thức chi tiết trong Bài 12: Đường thẳng và mặt phẳng song song giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:
Giải SBT Toán lớp 11 Bài 12: Đường thẳng và mặt phẳng song song
Bài 4.24 trang 63 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi G và H lần lượt là trọng tâm của hai tam giác ABC và ACD. Chứng minh rằng GH//(BCD)
Lời giải:
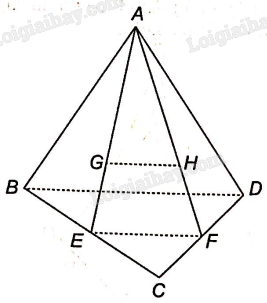
Gọi E, F lần lượt là trung điểm của các cạnh BC, CD. Vì G là trọng tâm của tam giác ABC nên A, G, E thẳng hàng và
Tương tự ta có A, H, F thẳng hàng và
Do đó,
Trong tam giác AEF có: , theo định lí Thalès đảo ta có GH//EF, mà nên GH//(BCD)
Xem thêm lời giải sách bài tập Toán lớp 11 Kết nối tri thức hay, chi tiết khác:
Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác:
Bài 11: Hai đường thẳng song song
Bài 12: Đường thẳng và mặt phẳng song song
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
