Với giải sách bài tập Toán 11 Bài 14: Phép chiếu song song sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:

Giải SBT Toán 11 Bài 14: Phép chiếu song song

Bài 4.41 trang 71 SBT Toán 11 Tập 1: Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M là điểm thuộc cạnh BC sao cho $MB=2MC.$

a) Xác định hình chiếu M’ của M qua phép chiếu song song lên mặt phẳng (A’B’C’) theo phương AA’.

b) Chứng minh rằng $M^{\prime }{B}^{\prime }=2M^{\prime }{C}^{\prime }$

Lời giải:

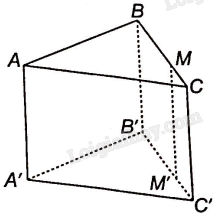
a) Trong mặt phẳng (BCC’B’) vẽ MM’//BB’ (M’ thuộc B’C’) thì M’ là hình chiếu của M qua phép chiếu đã cho.

b) Vì AA’//BB’//CC’ nên B’, C’ lần lượt là hình chiếu của B, C lên mặt phẳng (A’B’C’) theo phương chiếu AA’. Theo tính chất của phép chiếu song song suy ra $\frac{M^{\prime }{B}^{\prime }}{M^{\prime }{C}^{\prime }}=\frac{MB}{MC}=2$, suy ra $M^{\prime }{B}^{\prime }=2M^{\prime }{C}^{\prime }$

Bài 4.42 trang 71 SBT Toán 11 Tập 1: Cho hình lăng trụ tứ giác ABCD.A’B’C’D’. Gọi O là giao điểm của AC và BD. Gọi O’ là hình chiếu của O qua phép chiếu song song lên mặt phẳng (A’B’C’D’) theo phương AA’. Chứng minh rằng O’ là giao điểm của A’C’ và B’D’.

Lời giải:

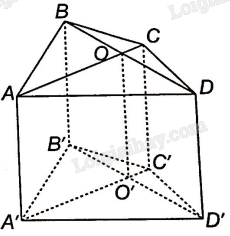
Qua phép chiếu lên mặt phẳng (A’B’C’D’) theo phương AA’, các điểm A, B, C, D, O lần lượt có hình chiếu là A’, B’, C’, D’, O’. Vì phép chiếu song song bảo toàn tính thẳng hàng của các điểm và O nằm giữa A và C nên O’ nằm giữa A’ và C’; Vì phép chiếu song song bảo toàn tính thẳng hàng của các điểm và O nằm giữa B và D nên O’ nằm giữa B’ và D’. Vậy O’ là giao điểm của A’C’ và B’D’.

Bài 4.43 trang 71 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD không là hình thang.

a) Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD)

b) Xác định hình chiếu của điểm A qua phép chiếu song song lên mặt phẳng (SCD) theo phương SB.

Lời giải:

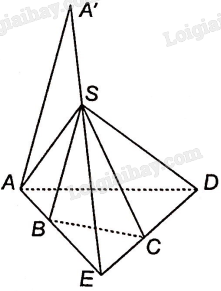
 a) Trong mặt phẳng (ABCD), gọi E là giao điểm của AB và CD. Khi đó, SE là giao tuyến của hai mặt phẳng (SAB) và (SCD).

b) Trong mặt phẳng (SAB), vẽ đường thẳng đi qua A và song song với SB cắt SE tại A’. Khi đó A’ là hình chiếu của điểm A qua phép chiếu đã cho.

Bài 4.44 trang 71 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và (P) là mặt phẳng cố định không song song với MN. Gọi A’, B’, C’, D’, M’, N’ lần lượt là hình chiếu của A, B, C, D, M, N qua phép chiếu lên mặt phẳng (P) theo phương MN.

a) Chứng minh rằng hai điểm M’ và N’ trùng nhau.

b) Chứng minh rằng bốn điểm A’, B’, C’, D’ là bốn đỉnh của một hình bình hành.

Lời giải:

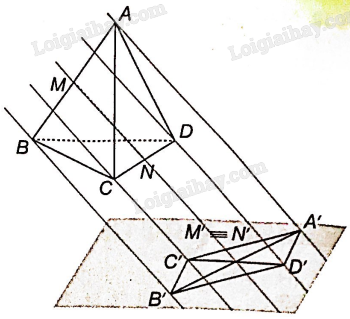
a) Vì đường thẳng MN là phương chiếu nên M’ của M trùng với hình chiếu N’ của N.

b) Vì M là trung điểm của AB nên theo tính chất của phép chiếu song song suy ra M’ là trung điểm của A’B’.

Vì N là trung điểm của CD nên theo tính chất của phép chiếu song song suy ra N’ là trung điểm của C’D’.

Vì M’ trùng N’ nên tứ giác tạo bởi bốn điểm A’, B’, C’, D’ có các đường chéo đi qua trung điểm của mỗi đường, suy ra tứ giác đó là hình bình hành.

Bài 4.45 trang 71 SBT Toán 11 Tập 1: Vẽ hình biểu diễn của hình chóp S.ABCD có đáy ABCD là hình vuông.

Lời giải:

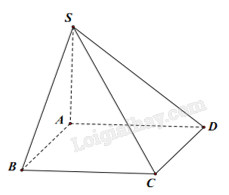
Vì đáy ABCD là hình vuông nên hình biểu diễn của hình vuông ABCD trong không gian là hình bình hành.

Hình biểu diễn của hình chóp S.ABCD có đáy ABCD là hình vuông trong không gian là:

Bài 4.46 trang 71 SBT Toán 11 Tập 1: Trong các hình sau, hình nào là hình biểu diễn của lăng trụ tứ giác có hai đáy là hình thang?

Lời giải:

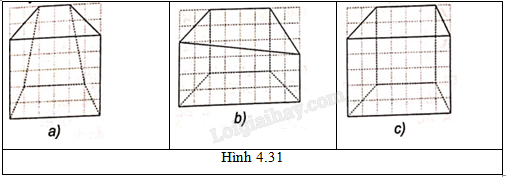
Hình biểu diễn của lăng trụ tứ giác có hai đáy là hình thang là hình 4.31c.

Bài 4.47 trang 71 SBT Toán 11 Tập 1: Ba chiếc gậy được đặt dựa vào tường và đôi một song song với nhau (H.4.32). Giải thích vì sao nếu ba đầu gậy trên tường thẳng hàng thì ba đầu gậy trên sàn cũng thẳng hàng.

Lời giải:

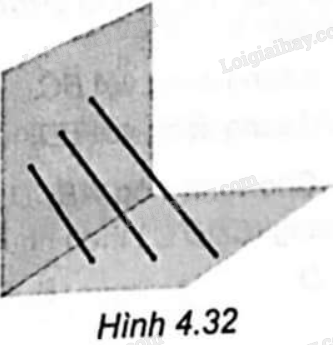
Gọi d là đường thẳng song song với ba chiếc gậy và (P) là mặt sàn. Khi đó ba đầu gậy trên sàn chính là hình chiếu của ba đầu gậy trên tường qua phép chiếu lên mặt phẳng (P) theo phương d. Vì phép chiếu song song bảo toàn tính thẳng thàng của các điểm nên nếu ba đầu gậy trên tường thì ba đầu gậy trên sàn cũng thẳng hàng.

Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài 13: Hai mặt phẳng song song

Bài 14: Phép chiếu song song

Bài tập cuối chương 4

Bài 15: Giới hạn của dãy số

Bài 16: Giới hạn của hàm số

Lý thuyết Phép chiếu song song

1. Phép chiếu song song

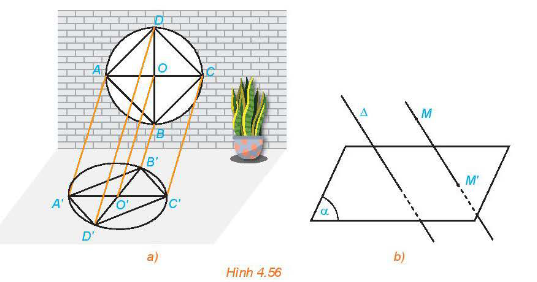
Cho mặt phẳng $\left(\alpha \right)$và đường thẳng $\mathrm{\Delta }$ cắt $\left(\alpha \right)$. Với mỗi điểm M trong không gian ta xác định điểm M’ như sau:

- Nếu M thuộc$\mathrm{\Delta }$ thì M’ là giao điểm của $\left(\alpha \right)$ và $\mathrm{\Delta }$.

- Nếu M không thuộc $\mathrm{\Delta }$ thì M’ là giao điểm của $\left(\alpha \right)$ và đường thẳng qua M song song với $\mathrm{\Delta }$.

- Điểm M’ được gọi là hình chiếu song song của điểm M trên mặt phẳng $\left(\alpha \right)$ theo phương $\mathrm{\Delta }$.

- Phép đặt tương ứng mỗi điểm M với hình chiếu M’ của nó được gọi là phép chiếu song song lên $\left(\alpha \right)$theo phương $\mathrm{\Delta }$.

- Mặt phẳng $\left(\alpha \right)$ được gọi là mặt phẳng chiếu, phương $\mathrm{\Delta }$gọi là phương chiếu.

- Cho hình $\mathrm{\Re }$, tập hợp các hình chiếu ${\mathrm{\Re }}^{\prime }$của các điểm M thuộc $\mathrm{\Re }$qua phép chiếu song song được gọi là hình chiếu của $\mathrm{\Re }$ qua phép chiếu song song đó.

2. Tính chất của phép chiếu song song

- Phép chiếu song song biến 3 điểm thẳng hàng thành 3 điểm thẳng hàng và không làm thay đổi thứ tự 3 điểm đó.

- Phép chiếu song song biến đường thẳng thành đường thẳng, tia thành tia, đoạn thẳng thành đoạn thẳng.

- Phép chiếu song song biến 2 đường thẳng song song thành 2 đường thẳng song song hoặc trùng nhau.

- Phép chiếu song song giữ nguyên tỉ số độ dài của hai đoạn thẳng cùng nằm trên một đường thẳng hoặc nằm trên hai đường thẳng song song.

3. Hình biểu diễn của một hình không gian

Hình biểu diễn của một hình không gian là hình chiếu song song của hình đó trên một mặt phẳng theo phương chiếu nào đó hoặc hình đồng dạng với hình chiếu đó.